2.2. Различные формы записи задач линейного программирования
Общей задачей линейного программирования, заданной в произвольной форме записи, называют задачу, в которой требуется максимизировать (минимизировать) линейную функцию.
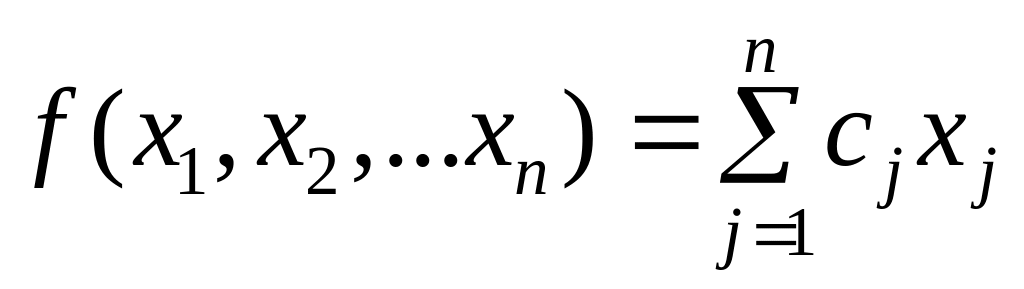, (2.32)
при условии
, (2.33)
. (2.34)
Функция (2.32) – целевая, а условия (2.33) – (2.34) – ограничения.
Задачей линейного программирования, заданной в симметричной форме записи, называют задачу, в которой требуется найти max функции (2.32) при условиях (2.33) и условиях
. (2.35)
Задачей линейного программирования в канонической форме записи называют задачу, в которой требуется найти максимум функции (2.321) при условиях (2.34), где s=0 и (2.35).
Набор
чисел
,
удовлетворяющих ограничениям задачи
линейного программирования, называется
ее планом.
План
,
доставляющий максимум (минимум) функции
(2.32) называют оптимальным.
Пример 2.6. Свести к симметричной форме записи следующую задачу, заданную в канонической форме.
,
(min)
, 
.
Решение.
Перейдем
от функции
к функции
и тем самым от задачи минимизации
–
к задаче максимизации
.
Систему ограничительных уравнений приведем к разрешенной форме, выделив некоторый базис переменных. Затем, опустив базисные переменные, перейдем к эквивалентной системе неравенств. Для завершения преобразований останется выразить целевую функцию через переменные, вошедшие в полученную систему неравенств.
Описанные преобразования системы ограничений в целевой функции удобнее проводить одновременно, приписав к жордановой таблице снизу строку для целевой функции ( - строку). В процессе жордановых исключений эту строку не следует выбирать разрешающей, но преобразовывать ее элементы нужно по обычным правилам. В результате целевая функция, как и базисные переменные, окажется выраженной через свободные переменные (табл. 2.10 – 2.13).
Таблица 2.10
|
1 |
|
|
|
|
|
|
0= 0= 0= |
12 16 19 |
0
1 |
1 2 2 |
2 1 2 |
-4 2 -1 |
-1 2 3 |
-3 -3 -5 |
= |
7 |
-2 |
1 |
-5 |
8 |
-1 |
3 |
Таблица 2.11
|
1 |
|
|
|
|
|
0= = 0= |
12 16 3 |
1 2 0 |
2 1
|
-4 2 -3 |
-1 2 1 |
-3 -3 -2 |
- = |
39 |
5 |
-3 |
12 |
3 |
-3 |
Таблица 2.12
|
1 |
|
|
|
|
0= = = |
6 13 3 |
2 0 |
2 5 -3 |
-3 1 1 |
1 -1 -2 |
- = |
48 |
5 |
3 |
6 |
-9 |
Таблица 2.13
|
1 |
|
|
|
= |
6 1 3 |
2 1 -3 |
-3 7 1 |
1 -3 -2 |
- = |
18 |
-7 |
21 |
-14 |
В условиях данной задачи разрешающие элементы можно выбирать произвольно.
Учитывая неотрицательность базисных переменных , , в табл. 2.13 опускаем их и приходим к эквивалентной системе неравенств, а вместе с тем и к симметричной форме записи задачи:
, (max)
, 
, 
.
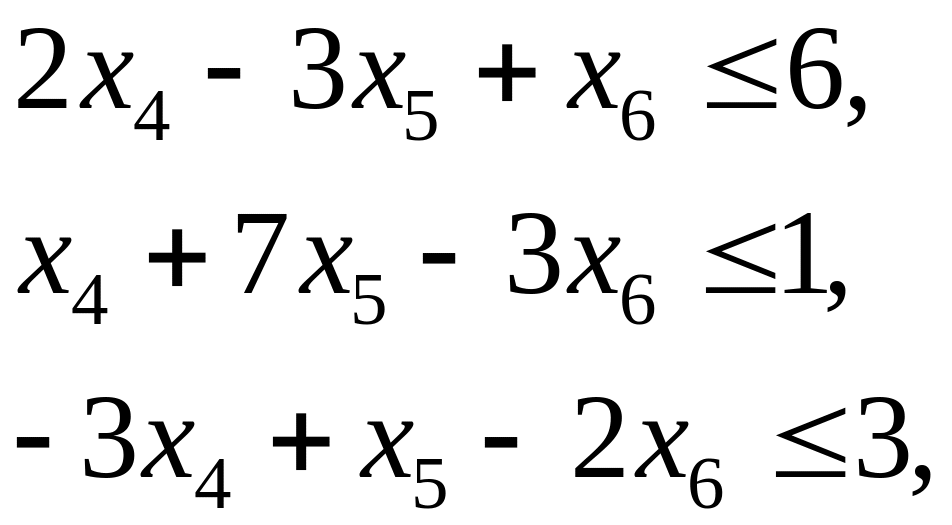