1.2Решение слау методом жордановых исключений

Пусть имеем систему m линейных алгебраических уравнений с n неизвестными:

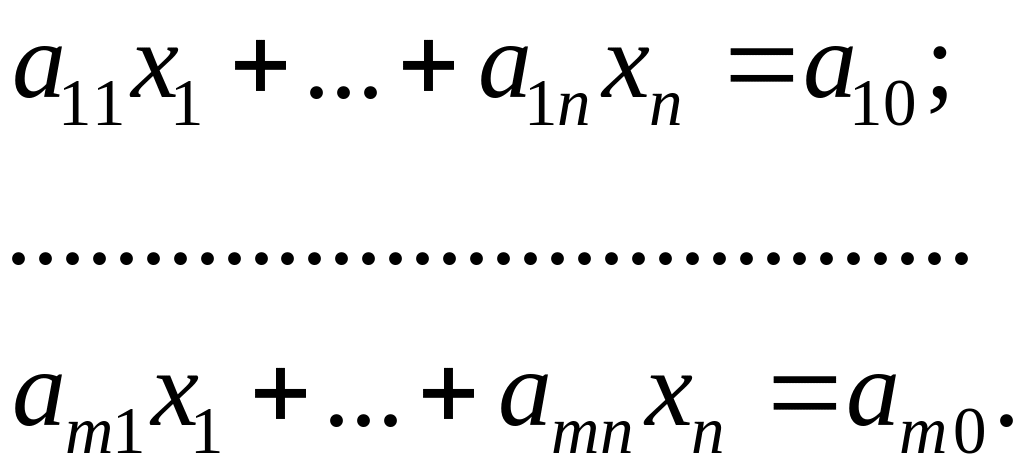(1.6)

Представим СЛАУ в виде нуль-равенств:

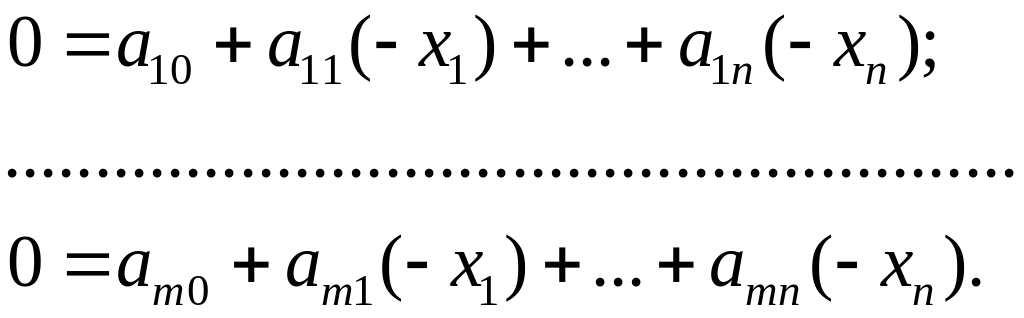
Полученную систему представим в форме жордановой таблицы (табл.1.6):

Таблица 1.6

	1		···
0=			···
···	···	···	···	···
0=			···

Пусть ранг матрицы коэффициентов размерности равен r. В этом случае можно произвести лишь r последовательных шагов жордановых исключений. В результате получим следующую жорданову таблицу:

Таблица 1.7

	1	0	···	0		···
			···			···
···	···	···	···	···	···	···	···
			···			···
0=			···		0	···	0
···	···	···		···	···	···	···
0=			···		0	···	0

Система (1.6) совместна тогда и только тогда, когда для некоторой совокупности x₁,…,x_n выполняются одновременно все равенства (1.6). Это возможно в том и только в том случае, если в табл. 1.7 . Если же хотя бы один из свободных членов отличен от нуля, то система (1.6) несовместна.

Если СЛАУ (1.6) совместна, из табл. 1.7 получаем её общее решение:

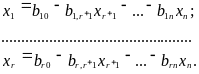(1.7)

При решении СЛАУ столбцы под переброшенными в верхнюю часть таблицы нулями (т.е. разрешающие столбцы) опускают.

Придавая в равенствах (1.7) свободным переменным произвольные значения  вычисляют соответствующие значения остальных неизвестных:

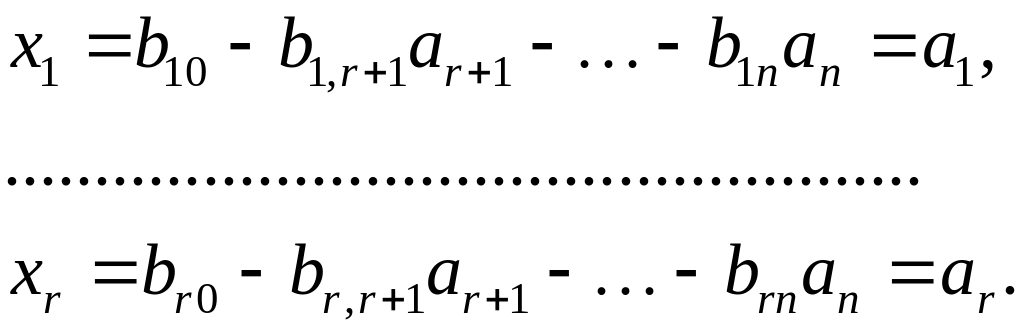
Таким образом, получено частное решение СЛАУ ( ). В результате СЛАУ имеет бесконечное множество решений.

Если же , через n шагов жордановых (модифицированных) исключений все переменные окажутся в левом заглавном столбце табл. 1.7, а их место вверху таблицы займут нули, и СЛАУ будет иметь единственное решение

Таким образом, для решения СЛАУ методом жордановых исключений необходимо выполнить следующее. Сначала следует записать СЛАУ в форме жордановой таблицы. Затем следует выполнить максимальное число шагов жордановых исключений, вычёркивая после каждого шага разрешающий столбец и строки, если они состоят целиком из нулевых элементов. Если в ходе исключений появится строка, все элементы которой, кроме свободного члена, равны нулю, то данная система несовместна. В противном случае СЛАУ совместна. При этом она имеет бесконечное множество решений, если в верхней части таблицы останется хотя бы одна переменная, и единственное решение, если все переменные окажутся в левом заглавном столбце.

Задача 1.2. Найти решение системы

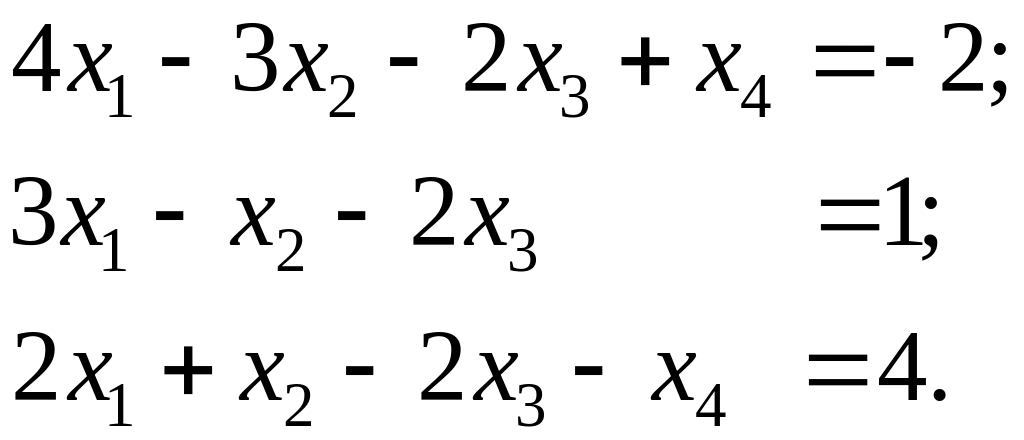
Решение. Запишем СЛАУ в форме жордановой таблицы

Таблица 1.8

	1				–
0=	-2	4	-3	-2	1
0=	1	3	-1	-2	0
0=	4	2		-2	-1

В качестве разрешающего элемента возьмём 1 и выполним первые два шага жордановых исключений; тогда будем иметь:

Таблица 1.9 Таблица 1.10

	1		–
0=	0	0	0
	1
	2

	1			–
0=	10	10	-8	-2
0=	5		-4	-1
x2=	4	2	-2	-1

Из табл. 1.10 выпишем общее решение.