Двумерные фильтры с искусственными задержками сигналов

Рассмотренные выше фильтры нацелены на пропускание волн с высокими кажущимися скоростями и подавление волн с низкими скоростями. Если полезные волны имеют V^*<<  , то для их выделения используются фильтры с искусственными задержками сигналов. Разделение (селекция) волн по параметру кажущейся скорости (по направлению подхода) является частным случаем  - р преобразования и описывается прямым интегральным преобразованием Радона. Суть его сводится к следующему.

Оцифрованные трассы сейсмограмм и временных разрезов по существу представляют собой табулированные значения двумерных функций f(t,x). Преобразование Радона (плосковолновое разложение) предполагает, что на локальном участке поля (t,x), отождествляемым с базой обработки двумерного фильтра, годограф регулярной волны удовлетворительно (с погрешностью, не превышающей погрешность определения времени) аппроксимируется линейной зависимостью вида t(x) = xp₀ + ₀. Прямое преобразование Радона заключается в вычислении на этом участке поля (t,x) функции двух новых переменных р и :

F_R(p,) =  f(x,px+)dx = (37) где х_нач, х_кон – границы области удовлетворительной линейной аппроксимации годографа. Схематически приведенное выше преобразование может быть представлено как:

Применительно к обработке дискретизированной информации выражение (37) преобразуется к виду: F_{R p,} = , где N – число трасс на базе обработки. (38) Из (38) видно, что осуществляется суммирование отсчетов всех трасс базы, распределенных вдоль линейного направления t(x) = xp₀ + ₀ (наклонное или направленное суммирование). Результатом обработки будет суммарная трасс с параметром направления суммирования р.

Комплексную частотную характеристику направленного суммирования на основании равенства (29) можно записать как: H(, t, p) =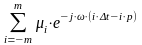 , (39) здесь параметр р равен величине задаваемой искусственной временной задержки между соседними трассами базы анализа. Очевидно, что максимальное значение H(, t) будет наблюдаться при it = ip. Задавая различные значения параметра р можно выделять волны с различными значениями V^*, т.е. управлять характеристикой направленности многомерного фильтра. Алгоритм направленного суммирования был предложен Ф. Рибером (США) в 1936 г., но развит и доведен до уровня промышленного метода сейсморазведки коллективом авторов под руководством Л.А. Рябинкина (метод регулируемого направленного приема сейсмических колебаний, МРНП). В классическом варианте МРНП конечной задачей обработки являлось получение по каждой сейсмограмме набора суммотрасс (суммолента) РНП, осуществлявших селекцию волнового поля по направлениям подхода волн (по V^*). Пример получения суммоленты МРНП, заимствованный из книги В.В. Знаменского «Общий курс полевой геофизики», приведен ниже.

Развитием этого подхода явились алгоритмы вычитания волн-помех в заданном диапазоне V^* (заданном диапазоне параметра р). Обрабатываемые сейсмограммы подвергаются -р преобразованию, затем суммотрассы заданном диапазоне параметра р обнуляются и по ним выполняется обратное преобразование.

Наиболее полно возможности направленного суммирования использованы в комплексе программ параметрической обработки сейсморазведочной информации SWAP, разработанным коллективом авторов под руководством Ю.Н. Воскресенского. Он позволяет не просто ослаблять волны в заданном диапазоне V^*, но полностью исключать их из волнового поля.