5.2.1. Пространственно-стационарная неоптимальная фильтрация Полевые интерференционные системы и веерные фильтры

Под полевыми интерференционными системами понимаются групповые источники и группы приемников. Веерные фильтры являются их лабораторным аналогом. Сущность алгоритма этого вида фильтров можно уяснить на примере линейной продольной равномерной интерференционной системы. Пусть система имеет нечетное число элементов М = 2m + 1 с шагом между ними, равным х. Чувствительность элементов _i, где i – номер элемента (- m  i  m), результат фильтрации будет отнесен к центральному элементу системы (i = 0). Упругие волны на базе системы, равном 2m могут считаться идеально-регулярными.

Пусть некоторая волна, имеющая кажущуюся скорость V^* создает в центральном элементе сигнал f₀(t) = ₀f(t). Тогда сигнал на i-том элементе будет

f_i(t) = _if(t – t_i) = _if(t – x_i / V^*) = _if(t – ix / V^*) = _if(t – it), (27) где t = x / V^*.

Сигнал на выходе системы f _вых (t) = = .

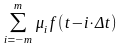В частотной области f(t)  S() и f _вых (t)  S_вых(). Согласно теореме запаздываний S_вых(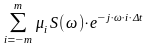) = = S()H(, t) (28) где H(, t) =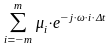 – комплексная частотная характеристика системы. (29)

Из выражения (29) видно, что максимальное значение комплексной частотной характеристики, равное H(, t) =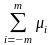 , достигается при t  0 (V^* ∞), т.е. рассматриваемая интерференционная система наилучшим образом пропускает волны с высокими кажущимися скоростями и ослабляет волны с низкими значениями кажущихся скоростей.

Заменяя в показателе степени экспоненциального члена выражения (29) произведение t = 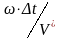= k_xx можно получить зависимость комплексной частотной характеристики от волнового числа k_x : H(w, Dt) = 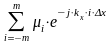(30)

Характеристику фильтра во временной области можно получить, применяя к H(w, Dt) преобразование Фурье: h(i,t) = (31) или в дискретной форме: h(i,t) = (32) где l – номер гармоники, _l – круговая частота l-ной гармоники,  = 1/(Nt) – шаг по частоте гармоник.

Для однородной интерференционной системы, где _i = const(i) (условно можно считать _i = 1), используя формулу Эйлера (e^{ j} = cos   jsin ), можно получить выражения для комплексной частотной характеристики в явном виде:

H(w, Dt) = 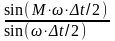или H(k_x, Dx) = (33)

Веерный фильтр

П

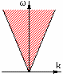
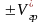ри работах МОВ область наблюдения тяготеет к пункту возбуждения. Поэтому кажущиеся скорости отраженных волн изменяются от  до (или 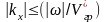). Тогда комплексную частотную характеристику веерного фильтра можно определить как:

H(w, k_x) =  1 при (34)

 0 при

Характеристику веерного фильтра во временной области можно получить используя двумерное Фурье-преобразование (19)

h(t,x) =

Последовательно применяя Фурье-преобразование с учетом пределов интегрирования (     по частоте и 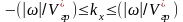по волновому числу) и значению H(w, k_x) в этих пределах (27), получим: h(t,x) = (35)

В дискретной форме: h_{x, i} = (36) где N, i – количество отсчетов на сейсмотрассе и номер отсчета;

t – шаг дискретизации;

 = 1/(Nt) – шаг по частоте гармоник.

Аналогичным образом можно построить режекторный веерный фильтр, вырезающий область

 1 при

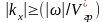
H(w, k_x) =  (30)

 0 при