Раздел 6. Элементы атомной физики и квантовой механики. Радиоактивность. Элементы квантовой статистики физики твердого тела Основные формулы

Первый постулат Бора (постулат стационарных

состояний с дискретными квантовыми значениями момента импульса)

mvr_n = nħ (n = 1,2,3…..),

где m – масса электрона,

v – скорость электрона на n-й стационарной орбите радиуса r_n,

ħ= h/2.

Второй постулат Бора (правило частот) при

переходе электрона с одной стационарной орбиты на другую.

h = E_n - E_m

Радиус n-й стационарной орбиты орбиты для

атом

1 2

а водорода по Бору

r_n = n²

(n = 1,2,3…..)

Дискретные значения энергии электрона в атоме водорода.

E_n =

Энергия кванта при переходе атома водорода из стационарного состояния n в состояние m с меньшей энергией.

h = E_n - E_m =

=

Потенциал ионизации атома водорода

_i =

Обобщенная формула для серий линий спектров атома водорода

= R ,

где  - длина волны спектральной линии,

R = - постоянная Ридберга,

m = 1,2,3, ..., n = m+1, m+2, ... .

Длина волны де Бройля

 = h/p,

где h - постоянная Планка,

p - импульс частицы.

Импульс частицы и его связь с кинетической

энергией Т:

для нерелятивистского случая

для релятивистского случая

где m_o - масса покоя частицы.

v - скорость частицы,

Е_о - энергия покоя частицы (Е_о = m_oc²).

p = m_ov, p = ,

p = ,

p = ,

Соотношение неопределенностей Гейзенберга

для координаты и импульса

где p_x - неопределенность проекции импульса

частицы на ось x,

x - неопределенность координаты частицы,

= h/2;

для энергии и времени

где E - неопределенность энергии частицы в некотором состоянии,

t - время жизни частицы в данном энергетическом состоянии.

p_xx  ,

3 4

Et  ,

Одномерное уравнение Шредингера для

стационарных состояний

где m - масса частицы,

Е - полная энергия частицы,

U = U(x) - потенциальная энергия частицы,

(x) - волновая функция, описывающая состояние частицы.

,

Плотность вероятности обнаружения частицы вблизи точки с координатой X на участке dx

w(x) = dW(x)/dx = (x)².

Вероятность обнаружения частицы в интервале

от x₁ до x₂

W = .

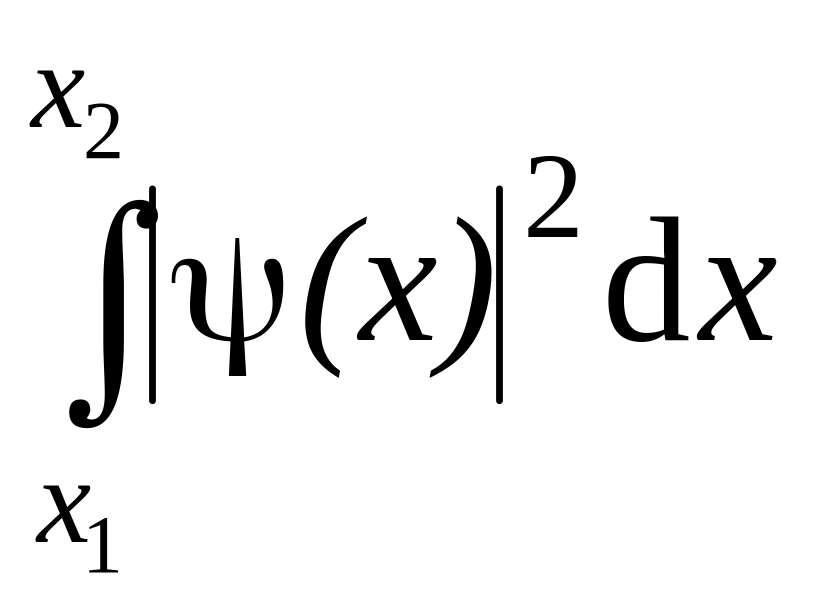Решение уравнения Шредингера для одномерной бесконечно глубокой потенциальной ямы

где n - квантовое число (n = 1,2,3, ...),

l - ширина ящика.

_n(x) = sin x,

Энергия частицы в одномерной бесконечно глубокой потенциальной яме

E_n = .

Собственная нормированная волновая функция электрона в атоме водорода в основном состоянии

где a_{о -} первый боровский радиус.

(r) = ,

Вероятность обнаружения электрона в атоме

водорода, находящемся в основном состоянии,

в интервале (r, r+dr)

dW = (r)²4r²dr.

Обобщенная формула для серий линий спектров водородоподобных атомов

где  - длина волны спектральной линии,

R - постоянная Ридберга,

Z - порядковый номер элемента,

n = 1,2,3, ..., k = n+1, n+2, ... .

= RZ² ,

Закон радиоактивного распада

где dN - число ядер, распадающихся за интервал за интервал времени dt,

N - число ядер, не распавшихся к моменту времени t,

N_o - начальное число радиоактивных ядер в момент времени t = 0,

 - постоянная радиоактивного распада.

d

5 6

N = - Ndt

или

N = N_oe^-t,

Число ядер, распавшихся за время t

N = N_o - N = N_o(1-e^-t).

Период полураспада радиоактивных ядер

T_1/2 = .

Среднее время жизни радиоактивного ядра

 = 1/.

Число атомов, содержащихся в радиоактивном

веществе

где m - масса вещества,

 - молярная масса вещества,

N_А - постоянная Авогадро.

N = N_A,

Активность радиоактивного вещества

где А_о = N_o - активность радиоактивного изотопа в начальный момент времени (t = 0).

А = -(dN/dt) = N =

= N_oe^-t = A_oe^-t,

Элементы дозиметрии:

Поглощенная доза (отношение поглощенной энергии излучения к массе облучаемого вещества).

Единица измерения поглощенной дозы -

1 Грей = 1 Дж/кг = 10² рад.

Мощность поглощенной дозы

Экспозиционная доза (величина, равная абсолютному заряду ионов одного знака, освобожденных квантами излучения в единице массы воздуха).

Единица измерения в системе СИ - 1Кл/кг. Внесистемной единицей измерения экспозиционной дозы служит рентген (Р): 1 Р = 2,5810^-4 Кл/кг, соответствующий образованию 2,0810⁹ пар ионов в 1 см³ сухого воздуха.

Мощность экспозиционной дозы

Эквивалентная доза излучения (суммарная поглощенная доза с учетом коэффициента качества излучения К, характеризующего относительную биологическую активность рассматриваемого излучения по сравнению с рентгеновским и гамма-излучениями. В системе СИ измеряется в Зивертах:

1 Зв = 1 Дж/кг. Внесистемной единицей эквивалентной дозы является Бэр: 1 Зв = 10² Бэр.

Мощность эквивалентной дозы

D = dE/dm;

P_D = dD/dt;

X = dQ/dm;

P_X = dX/dt;

Н = ;

P_Н = dН/dt.

Энергия связи ядра

где Z - зарядовое число (атомный номер) ядра,

А - массовое число ядра,

m_p - м

7 8

асса протона (в а.е.м.),

m_n - масса нейтрона (в а.е.м.),

m_я - масса ядра (в а.е.м.).

Е_св = c²{[Zm_p + (A-Z)m_n] -m_я} = 931,5{[Zm_p + (A-Z)m_n] -m_я} МэВ ,

Дефект массы ядра (в а.е.м.)

m = Zm_p + (A-Z)m_n] -m_я

Энергия ядерной реакции

где m₁ - масса покоя налетающей частицы,

m₂ - масса неподвижного ядра (мишени),

m_i^/ - сумма масс покоя частиц, образовавшихся в результате реакции (в а.е.м.).

Q = 931,5 (m₁ + m₂ - m_i^/) МэВ

Пороговая кинетическая энергия налетающей частицы, вызывающей ядерную реакцию

Т_п = Q.

Энергия Ферми в металле при Т = 0 К

где n - концентрация электронов в металле,

m_e- масса электрона.

Е_F = (3²n)^2/3,

Дано: =10 пм	в единицах СИ =110-11 м	Решение: Энергия электронов, бомбардирующих анод рентгеновской трубки, равна энергии рентгеновских квантов с длиной волны, соответствующей коротковолновой границе сплошного рентгеновского спектра, то есть
Найти:

Концентрация электронов, энергия которых

заключена в пределах от  до +d (при   Е_F)

dn() =

Удельная проводимость примесных

полупроводников

где e - элементарный заряд,

n_p и n_n - концентрация дырок и электронов,

b_p и b_n - подвижность дырок и электронов.

 = e(n_pb_p + n_nb_n),

Температурная зависимость проводимости в

полупроводниках

где Е - ширина запрещенной зоны,

_о - константа,

k - постоянная Больцмана.

 = _оexp ,