3. Погрешности. Виды погрешностей.

Погрешность – это отклонение измеренного значения искомой физической величины от ее истинного значения. Допускаемые при измерениях погрешности принято разделять на три вида: систематические, случайные и промахи.

Промахи (грубые ошибки) – это очевидные ошибочные измерения, значительно отличающиеся от результатов повторных измерений, близких между собой. Промахи могут быть обусловлены невнимательностью исследователя, неисправностью прибора, небрежностью записи и т.п. При обработке данных такой результат не учитывают и проводят повторные измерения.

Систематическими называют погрешности, которые при повторных измерениях остаются постоянными и отклоняют результат измерений в одну и ту же сторону: либо только в сторону увеличения, либо только в сторону уменьшения. Систематические ошибки могут быть учтены, если выявлена их причина.

Случайными называются погрешности, обусловленные множеством причин, не поддающихся контролю и учету, которые отклоняют измеренное значение от истинного как в сторону увеличения, так и в сторону уменьшения. Указанные погрешности можно уменьшить, но полностью их устранить невозможно.

Случайные ошибки подчиняются статистическим закономерностям и описываются теорией вероятности.

4. Определение случайных погрешностей при прямых измерений.

Обозначим через x₁, x₂, …x_n результаты измерений какой-либо величины. В таком случае наиболее вероятной, близкой к истинному значению, является величина, называемая средним арифметическим всех, полученных при измерениях значений.

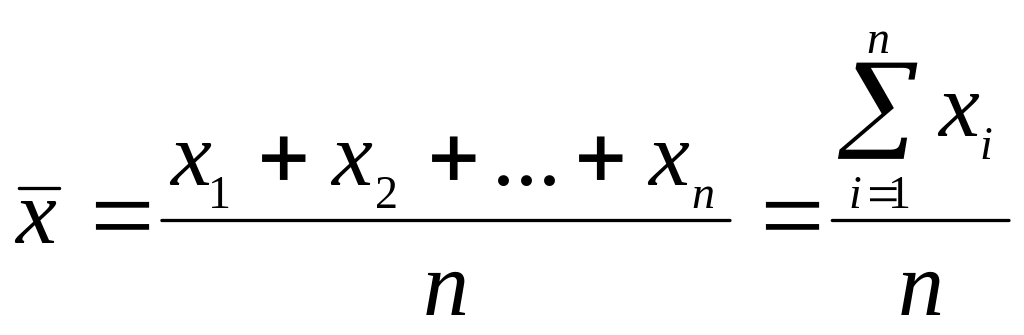, (1)

где п – число измерений.

Случайные отклонения в разные стороны равновероятны. Данный случай описывается нормальным распределением Гаусса.

Пусть х – случайная ошибка измерения величины х. Это непрерывная случайная величина, подчиняющаяся определенному закону распределения. Введем (х) – плотность распределения вероятности ошибки х. Ошибки разных знаков равновероятны. Чем больше ошибка по абсолютной величине, тем меньше ее вероятность, т.е. (х) монотонно убывает при возрастании х. На рис.1 изображено нормальное распределение Гаусса:

, (2)

г де ² – дисперсия величины х.

рис.1 рис.2

Дисперсия характеризует разброс случайных величин х, так как является параметром кривой распределения. При большей дисперсии кривая расплывается, менее – ярко выражен максимум, более вероятны большие отклонения (рис.2).

Так как случайные ошибки имеют статистический характер, то можно только найти только вероятность появления той или иной ошибки по формуле (2).

Вероятность того, что измеряемая величина содержится в интервале , называется надежностью р (соответствующей х).

Абсолютно точное значение измеряемой величины определить невозможно, потому в качестве измеряемой величины рассматривают его среднее значение . Результат измерений записывают в виде:

и обязательно указывают достоверность этого результата р. Такая запись показывает в каких пределах содержится истинное значение измеряемой величины с определенной надежностью.

Для оценки допущенной ошибки необходимо знать квадратный корень из дисперсии метода измерений. Но при практических измерениях не существует аналитических формул для определения дисперсии, поэтому дисперсию определяют экспериментально по допущенным абсолютным ошибкам.

Абсолютной погрешностью отдельного измерения |х_i| называется взятая по модулю разность между отдельно измеренным значением х_i и средним арифметическим :

|х₁| = |х₁ – | (3)

. . . . . . . . . . . . .

|х_п| = |х_п – |

Абсолютная погрешность отдельного измерения имеет ту же размерность, что и измеряемая величина.

Среднюю абсолютную погрешность | | вычисляют как среднее арифметическое абсолютных погрешностей отдельных измерений х_i, взятых по модулю:

(4)

Средняя квадратичная ошибка (отклонение) равняется квадратному корню из дисперсии измерений . Дисперсия равна:

Практически n выбирают конечным и в качестве дисперсии рассматривают ее приближенное значение. Тогда средняя квадратичная ошибка равна:

(5)

То есть чем больше число измерений, тем меньше значение (5).

В 1908 г. Боссет (псевдоним «Стьюдент») доказал, что статистический подход справедлив и при малом числе измерений. Распределение Стьюдента при числе измерений n переходит в распределение Гаусса, а при малом числе измерений мало отличается от него (рис.3). Функция распределения Стьюдента табулирована. Определив среднюю квадратичную ошибку  из (5) и параметр распределения t:

, (6)

по таблице можно определить достоверность р.

Точность измерений характеризуется относительной погрешностью Е, которая показывает, какую долю измеренной величины составляет средняя абсолютная погрешность. Точность вычисляется как отношение средней абсолютной погрешности  к среднему арифметическому :

Е =  (7)

Она выражается как в процентах, так и относительных единицах.

Относительная погрешность позволяет производить сравнение точности измерений физических величин и методов, которые при этом применяются. Знаки «» указывают, что погрешность может, как увеличивать, так и уменьшать результат измерений.

Пример. В результате измерений диаметра d абразивных зерен получены следующие значения: d₁ = 2,83мкм; d₂ = 2,82мкм; d₃ = 2,81мкм; d₄ = 2,85 мкм; d₅ = 2,87 мкм. Найти среднее арифметическое значение и оценить точность измерений, достоверность результата.

Дано: Решение.

d ₁ = 2,83 мкм 1. Среднее арифметическое находим по формуле:

d₂ = 2,82 мкм

d₃ = 2,81 мкм 2. Подставляем числовые значения:

d₄ = 2,85 мк м

d₅ = 2,87 мк м 3. Находим абсолютные погрешности отдельных измерений:

п = 5 |d₁| = |d₁ – | = |2,83 – 2,836| = |0,006| (мкм)

– ? Е – ? |d₂| = |d₂ – | = |2,82 – 2,836| = |0,016| (мкм)

|d₃| = |d₃ – | = |2,81 – 2,836| = |0,026| (мкм)

|d₄| = |d₄ – | = |2,85 – 2,836| = |0,014| (мкм)

|d₅| = |d₅ – | = |2,87 – 2,836| = |0,034| (мкм)

4. Вычисляем среднюю абсолютную погрешность | | по формуле:

| | =

| | = .

5. Вычисляем относительную погрешность:

Е =  100% =  100% = 0,7%.

6. Рассчитываем среднеквадратичное отклонение:

,

7. Подставляем числовые значения:

8. Рассчитываем параметр t:

9. По таблице Стьюдента определяем параметры t₁, t₂ и достоверности p₁,p₂:

t₂ > t > t₁: t₁ = 1,5 и t₂ = 2

p₁ = 0,78 и p₂ = 0,884.

10. Рассчитываем достоверность результата по формуле:

,

11. Окончательный результат записываем в виде доверительного интервала, в середине которого находится истинное значение диаметра:

2,836 – 0,019  d  2,836 + 0,019 (мкм)

2,817  d  2,855 (мкм).

Ответ: диаметр d = (2,836  0,019) мкм при Е = 0,7% и достоверности р = 0,838.

5. Определение случайных погрешностей при косвенных измерениях. В большинстве случаев при проведении измерений исследуемая физическая величина не может быть непосредственно измерена, а является функцией одной или нескольких величин, которые измеряют с помощью прямых методов.

Пусть для нахождения величины x пришлось измерить величины m, n, k. Величины x, m, n, k связаны функциональной зависимостью x = f (m, n, k).

В этом случае средняя абсолютная ошибка  x_ср может быть найдена по правилам дифференцирования, если знак дифференциала d заменить знаком ошибки  и выбрать знаки таким образом, чтобы величина ошибки была максимальной, т.е.

(8)

и (9)

В частности, если зависимость имеет вид x = f (m), то формула (8) имеет вид:

.

относительная ошибка находится по формуле (7):

Е = ,

а так как дифференциал натурального логарифма

, (10)

то

или

(11)

Таким образом, относительная ошибка результата равна полному дифференциалу натурального логарифма функции, определяющей зависимость данной величины от измеряемых величин. При вычислении надо брать сумму абсолютных значений дифференциалов всех членов логарифма (все частные ошибки складываются) с заменой знаков d на .

Относительную ошибку измерения следует вычислять в такой последовательности:

1. прологарифмировать расчетную формулу;

2. найти от логарифма полный дифференциал;

3. если ошибка отдельных измерений входит в результат дифференцирования несколько раз, то надо сгруппировать все члены, содержащие одинаковый дифференциал и выражения в скобках, стоящие перед дифференциалом, взять по модулю; знак d заменить на ; знаки выбирают так, чтобы абсолютная величина относительной ошибки была максимальной.

Пример. При определении модуля Юнга расчетная формула имеет вид:

,

где ℓ – длина исследуемого стержня, a – ширина поперечного сечения стержня,

b – высота (толщина) стержня, – отношение стрелы прогиба к величине нагрузки.