
§ 4. Логарифмическое дифференцирование
Лемма.
Если
 дифференцируема в точке
,
то
дифференцируема в точке
.
дифференцируема в точке
,
то
дифференцируема в точке
.
Доказательство.
Представим
функцию
следующим образом:
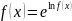 и применим теорему о дифференцируемости
сложной функции. Внутренняя функция
дифференцируема в точке
по условию леммы, внешняя функция
и применим теорему о дифференцируемости
сложной функции. Внутренняя функция
дифференцируема в точке
по условию леммы, внешняя функция
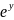 дифференцируема всюду в
,
следовательно, сложная функция
дифференцируема всюду в
,
следовательно, сложная функция
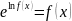 дифференцируема в точке
,
причем
дифференцируема в точке
,
причем
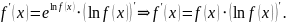
степенной функциям.
1)
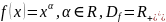 .
.
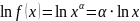 -
дифференцируемая в
функция, причем
-
дифференцируемая в
функция, причем
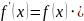 .
.
Итак,
для любого
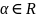
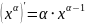 .
.
2)
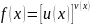 .
.
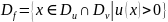 .
.
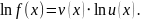
Пусть
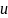 и
и
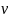 дифференцируемы в точке
дифференцируемы в точке
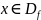 .
Тогда
.
Тогда
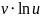 дифференцируема в точке
дифференцируема в точке
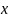 ,
а значит и
,
а значит и
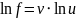 дифференцируема в точке
.
Следовательно,
дифференцируема
в точке
,
причем
дифференцируема в точке
.
Следовательно,
дифференцируема
в точке
,
причем
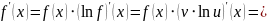
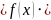
Следовательно:
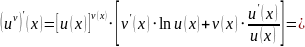
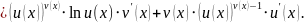
Итак: производная от показательно-степенной функции равна сумме производной от этой функции, рассматриваемой как сложная показательная функция, и производной от этой функции, рассматриваемой как сложная степенная функция.
Примеры.
1)
 ,
,
 .
.
2)
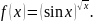
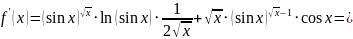
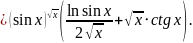
§ 5. Касательная и производная
В этом параграфе мы рассмотрим геометрический смысл производной.
Определение
1.
Касательной к плоской кривой
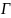 в точке
в точке
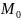 называется прямая
называется прямая
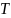 ,
проходящая через точку
и такая, что отрезок
,
проходящая через точку
и такая, что отрезок
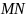 есть величина бесконечно малая в точке
более высокого порядка, чем отрезок
есть величина бесконечно малая в точке
более высокого порядка, чем отрезок
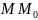 ,
т.е.
,
т.е.
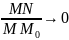 при
при
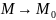
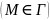 .
.
Лемма.
Прямая
является касательной к кривой
в точке
тогда и только тогда, когда угол
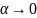 при
,
при
,
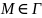 .
.
Доказательство.
1)
Пусть
- касательная к
в точке
,
т.е. по определению 1
при
.
Но
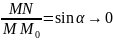 при
.
Т.к.
при
.
Т.к.
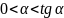 и
и
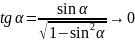 при
,
то по теореме о пределе «под конвоем»
при
.
при
,
то по теореме о пределе «под конвоем»
при
.
2)
Пусть
при
.
Требуется доказать, что прямая
является касательной к кривой
в точке
.
Действительно,
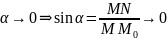 при
.
Следовательно по определению 1 прямая
является касательной к кривой
в точке
.
при
.
Следовательно по определению 1 прямая
является касательной к кривой
в точке
.
Рассмотрим связь между возможностью провести касательную к графику функции в некоторой точке и дифференцируемостью в этой точке.
Теорема
1.
Если
дифференцируема в точке
,
то к графику функции
в точке
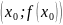 можно провести невертикальную касательную
с угловым коэффициентом
.
можно провести невертикальную касательную
с угловым коэффициентом
.
Доказательство.
По условию теоремы дифференцируема в точке , т.е.
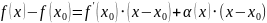 ,
где
,
где
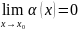 .
.
Требуется доказать, что прямая, проходящая через точку и имеющая угловой коэффициент является касательной к графику функции в этой точке. Заметим, что уравнение такой прямой имеет вид:
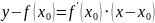
Покажем,
что
при
.
Имеем
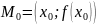 ,
,
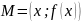 ,
,
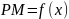 ,
,
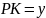 .
Тогда:
.
Тогда:
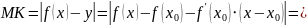
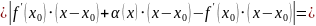
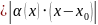
Оценим
отношение:
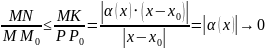 при
.
при
.
Итак, при . Т.о. доказано, что уравнение касательной к графику дифференцируемой функции в точке имеет вид
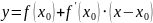 .
.
Теорема 2. Пусть непрерывна в точке и к графику функции в точке можно провести невертикальную касательную. Тогда дифференцируема в точке и совпадает с угловым коэффициентом касательной.
Доказательство.
Для
доказательства дифференцируемости
функции
в точке
достаточно показать, что
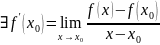 .
.
Рассмотрим
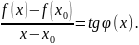 (1)
(1)
Очевидно,
что
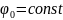 ,
а углы
и
зависят от
.
Т.к.
,
а углы
и
зависят от
.
Т.к.
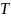 - касательная, то угол
при
(по лемме).
- касательная, то угол
при
(по лемме).
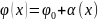 ,
как внешний угол треугольника.
Следовательно,
,
как внешний угол треугольника.
Следовательно,
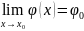 .
.
Угловой
коэффициент касательной
:
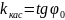 .
.
Угловой
коэффициент секущей
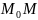 :
:
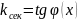 .
.
Т.к.
касательная
не является вертикальной, то
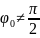 .
Функция
не определена в точке
(т.к., если
.
Функция
не определена в точке
(т.к., если
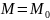 ,
то секущей нет). Доопределим
в точке
по непрерывности, т.е. положим
,
то секущей нет). Доопределим
в точке
по непрерывности, т.е. положим
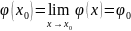 .
.
Рассмотрим
теперь сложную функцию
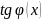 .
.
Функция
непрерывна
в точке
и
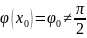 ;
функция
;
функция
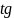 непрерывна
в точке
непрерывна
в точке
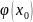 .
Следовательно, функция
.
Следовательно, функция
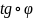 непрерывна в точке
и
непрерывна в точке
и
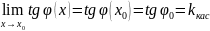 .
Отсюда с использованием (1) следует, что
.
Отсюда с использованием (1) следует, что
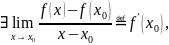
т.е.
дифференцируема в точке
,
причем
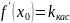 (2)
(2)
Если
уравнение касательной
имело вид
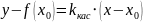 ,
то с учетом (2), получаем уравнение
невертикальной касательной в виде:
,
то с учетом (2), получаем уравнение
невертикальной касательной в виде:
Тогда уравнение нормали к графику функции в точке имеет вид:
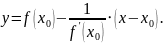
Из теорем 1 и 2 следует геометрический смысл производной функции в точке: вычислить значение производной функции в точке означает найти угловой коэффициент касательной, проведенной к графику функции в этой точке.
Примеры.
1)
.
Уравнение касательной в точке
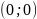 имеет вид
имеет вид
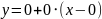 ,
т.е.
,
т.е.
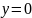 .
.
2)
.
Найдем угол пересечения графика с осью
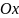 .
.
Возьмем
,
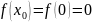 ,
,
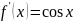 ,
,
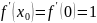 .
.
Уравнение
касательной к графику функции
в точке
имеет вид
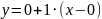 ,
т.е.
,
т.е.
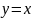 .
Т.о.,
.
Т.о.,
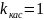 ,
т.е. искомый угол:
,
т.е. искомый угол:
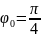 .
.
Аналогично
в точке
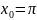 ,
,
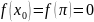 ,
,
 .
.
Уравнение
касательной к графику функции в точке
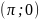 имеет вид
имеет вид
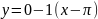 ,
т.е.
,
т.е.
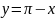 .
Т.о.,
.
Т.о.,
 ,
т.е. искомый угол:
,
т.е. искомый угол:
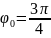 .
.
3) . Найдем угол пересечения графика с осью .
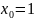 ,
,
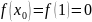 ,
,
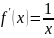 ,
,
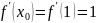 .
.
Уравнение
касательной к графику функции в точке
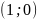 имеет вид
имеет вид
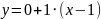 ,
т.е.
,
т.е.
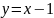 .
Т.о.,
,
т.е. искомый угол:
.
.
Т.о.,
,
т.е. искомый угол:
.
Замечание (о вертикальных касательных).
Рассмотрим
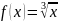 .
.
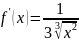 не определена в точке
,
т.е.
не дифференцируема в точке
.
не определена в точке
,
т.е.
не дифференцируема в точке
.
Вычислим
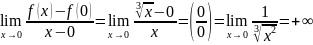
Если
учесть, что в точке
касательная к графику рассматриваемой
функции вертикальна и положить
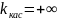 ,
то можно расширить понятие производной.
,
то можно расширить понятие производной.
Определение
2.
Мы скажем, что функция
имеет в точке
бесконечную производную, если
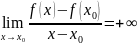 (или
(или
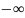 ).
).
В таком случае, если касательная к графику функции в точке вертикальна, то геометрический смысл производной сохраняется (она совпадает с угловым коэффициентом касательной).
Если
рассмотреть функцию
 ,
то здесь
,
то здесь
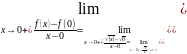
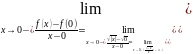
Здесь в точке бесконечная производная не существует.
