
Глава I. Дифференцируемость и производная
§1. Скорость
Рассмотрим
прямолинейное движение материальной
точки за промежуток времени от
 до
до
 .
Пусть в момент времени
.
Пусть в момент времени
 точка занимает на числовой прямой
положение
точка занимает на числовой прямой
положение
 ,
а в момент времени
,
а в момент времени
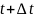 - положение
- положение
 .
Величину пройденного пути за промежуток
времени
.
Величину пройденного пути за промежуток
времени
 обозначим
обозначим
 .
Очевидно,
.
Очевидно,
 .
.
Определение 1. Движение называется равномерным, если пройденные пути пропорциональны затраченному времени, т.е.
 (1)
(1)
где
 - коэффициент пропорциональности,
называемый скоростью.
Из (1) следует, что
- коэффициент пропорциональности,
называемый скоростью.
Из (1) следует, что
 . (2)
. (2)
Теорема
1.
Движение, описываемое функцией
,
равномерно и прямолинейно тогда и только
тогда, когда
 можно задать формулой
можно задать формулой
 ,
где
,
где
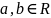 .
.
Доказательство.
1.
Пусть движение, описываемое функцией
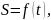 равномерно и прямолинейно. Рассмотрим
промежуток времени от
равномерно и прямолинейно. Рассмотрим
промежуток времени от
 до
до
 и обозначим
и обозначим
 ,
,
 .
Вычислим скорость по формуле (2):
.
Вычислим скорость по формуле (2):
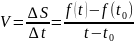
Тогда
 и, следовательно:
и, следовательно:
 .
.
Введем
обозначения:
 ,
,
 .
Получим:
,
где
.
.
Получим:
,
где
.
2.
Пусть закон движения задан формулой
 ,
где
,
где
 .
Тогда
.
Тогда
 .
Следовательно:
.
Следовательно:
 ,
,
т.е. пройденные пути пропорциональны затраченному времени, а это и означает, что движение является равномерным.
Рассмотрим теперь неравномерное движение. Известен первый закон Ньютона: «Всякое тело сохраняет свое механическое состояние до тех пор, пока какие-либо внешние силы не выведут его из этого состояния».
Рассмотрим
два случая для действующей силы
 .
.
 .
Движение тела будет равномерным, а
значит по теореме 1
.
Движение тела будет равномерным, а
значит по теореме 1
 ,
где
,
где
 ,
называемая
мгновенной скоростью.
,
называемая
мгновенной скоростью.
2.
Пусть, начиная с момента времени
,
 .
Тогда движение тела будет слагаться из
двух составляющих:
.
Тогда движение тела будет слагаться из
двух составляющих:
а) указанного равномерного движения,
б) того движения, которое вызвала сила , если бы скорость в момент времени равнялась 0 (т.е. если бы движение рассматривалось именно с этого момента времени).
Как показал Галилей, если бы равнодействующая сила, приложенная в момент времени , была бы постоянной, начиная с этого момента, и была бы направлена по этой же прямой, то пройденный путь был бы пропорционален этой равнодействующей и квадрату времени, т.е.
 ,
,
где
 и
и
 ,
,
 ,
,
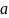 – ускорение.
– ускорение.
Очевидно,
 – бесконечно малая в точке
более высокого порядка, чем
.
Таким образом, закон прямолинейного
движения описывается функцией
– бесконечно малая в точке
более высокого порядка, чем
.
Таким образом, закон прямолинейного
движения описывается функцией
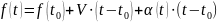 ,
(3)
,
(3)
где
 ,
.
Из формулы (3) определим:
,
.
Из формулы (3) определим:
 (4)
(4)
Величина,
описываемая формулой (4) – есть средняя
скорость движения за промежуток времени
от
до
.
Переходя к пределу в (4) при
 ,
получим:
,
получим:
|
(5) |
Формула (5) не есть определение мгновенной скорости! Она является следствием того, что – «почти линейна».
Замечание. Часто в учебниках по физике формулу (5) принимают за определение мгновенной скорости. Однако, понятие скорости возникло в XVI-XVII вв. задолго до появления понятия производной.
§2. Понятие дифференцируемой функции и производной
В
предыдущем параграфе мы рассмотрели
задачу о прямолинейном движении точки
и получили формулу для вычисления
мгновенной скорости движения. Эта
формула связана с отношением
 ,
где
- закон движения,
,
- время.
,
где
- закон движения,
,
- время.
Рассмотрим основные понятия теории дифференцирования функций одной действительной переменной и установим связь между этими понятиями и задачей о скорости, решенной нами в § 1.
Определение
1.
Функция
 называется дифференцируемой в точке
называется дифференцируемой в точке
 ,
если выполняются условия:
,
если выполняются условия:
1)
 - неизолированная точка
- неизолированная точка
 ,
,
2) приращение функции в окрестности точки представимо в виде
 , (1)
, (1)
где
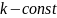 ,
,
 при
при
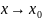 .
.
Определение 2. Пусть - неизолированная точка . Если существует

то
значение этого предела называют
производной функции
в точке
и обозначают
 .
Таким образом,
.
Таким образом,
|
(2) |
Замечание.
Т.к.
- неизолированная точка
и
 ,
то
- неизолированная точка
,
то
- неизолированная точка
 .
Можно переопределить значение
в точке
по непрерывности, положив
.
Можно переопределить значение
в точке
по непрерывности, положив

Определение
3. Пусть
функция
имеет производную в каждой точке
или некоторого подмножества
.
Производной функции
называется функция
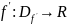 ,
где
,
где
 и
и
 для любого
для любого
 .
.
Рассмотрим примеры.
1)
 .
Покажем, что функция
дифференцируема в любой точке множества
.
Покажем, что функция
дифференцируема в любой точке множества
 .
Оценим приращение функции:
.
Оценим приращение функции:
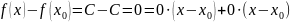 ,
,
здесь
 и
и
 .
Таким образом, в любой точке
.
Таким образом, в любой точке
 приращение функции представимо в виде
(1).
приращение функции представимо в виде
(1).
2)
 .
Покажем, что функция
дифференцируема в любой точке множества
.
Оценим приращение функции:
.
Покажем, что функция
дифференцируема в любой точке множества
.
Оценим приращение функции:
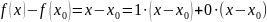 ,
,
здесь
 и
.
Таким образом, в любой точке
приращение функции представимо в виде
(1).
и
.
Таким образом, в любой точке
приращение функции представимо в виде
(1).
3)
 .
Покажем, что функция
дифференцируема в любой точке множества
.
Оценим приращение функции:
.
Покажем, что функция
дифференцируема в любой точке множества
.
Оценим приращение функции:
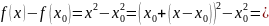
=
 ,
,
здесь
 и
и
 при
.
Таким образом, в любой точке
приращение функции представимо в виде
(1).
при
.
Таким образом, в любой точке
приращение функции представимо в виде
(1).
4)
 .
Найдем
.
Найдем
 ,
где
.
,
где
.

Таким
образом,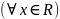
 .
.
Т.к. мгновенная скорость при неравномерном прямолинейном перемещении вычисляется по формуле

где
 - путь, то производная
- путь, то производная
 есть мгновенная скорость прямолинейного
движения, описываемого функцией
,
в момент времени
.
есть мгновенная скорость прямолинейного
движения, описываемого функцией
,
в момент времени
.
Рассмотрим основные свойства дифференцируемых функций.
Теорема 1. Если дифференцируема в точке , то непрерывна в точке .
Доказательство.
Т.к.
дифференцируема в точке
,
то
,
где
 и
при
.
Но тогда:
и
при
.
Но тогда:
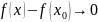 при
,
при
,
т.е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции в точке , а значит функция непрерывна в точке .
Обратная
теорема неверна! Например функция
 непрерывна в точке
непрерывна в точке
 ,
но не является дифференцируемой в этой
точке.
,
но не является дифференцируемой в этой
точке.
Теорема
2.
1) Если
дифференцируема в точке
,
то функция
имеет производную в точке
 .
.
2) Если функция имеет производную в точке , то дифференцируема в точке .
Доказательство.
1)
Т.к.
дифференцируема в точке
,
то
,
где
и
при
.
Пусть
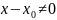 .
Тогда:
.
Тогда:

Переходя к пределу при , получим:

Таким
образом,
 .
.
2)
Пусть
 .
Т.е.
.
Т.е.


 ,
где
,
где
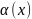 - бесконечно малая в точке
.
- бесконечно малая в точке
.
 . Доопределим
в точке
по непрерывности, т.е. положим
. Доопределим
в точке
по непрерывности, т.е. положим
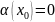 .
Тогда:
.
Тогда:
 ,
,
где
 и
при
.
Таким образом, функция
дифференцируема
в точке
.
и
при
.
Таким образом, функция
дифференцируема
в точке
.
Вернемся к примерам:
из
2) следует, что

из
3) следует, что
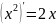
из 4) следует, что дифференцируема в любой точке .
Контрпример к теореме 1:
Рассмотрим функцию . И пусть . Покажем, что не является дифференцируемой в точке . Действительно:
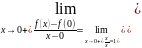

Т.к. односторонние пределы функции в точке не совпадают друг с другом, значит, предел функции в точке не существует:
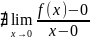
Т.е.
 ,
и, следовательно, по теореме 2 функция
не дифференцируема в точке
,
и, следовательно, по теореме 2 функция
не дифференцируема в точке
 .
.
Дифференцируемость – это локальное свойство функции (также, как непрерывность).


