Тема: Выявление основной тенденции развития в рядах динамики и прогнозирование

Задание:В целях выявления основной тенденции провести выравнивание ряда динамики выпуска продукции «А» на предприятии методом наименьших квадратов по различным уравнениям. (См. исходные данные в соответствии с вариантом)

Вычислить остаточные средние квадратические отклонения фактических уровней от выравненных;

Выбрать уравнение, которое наиболее точно отражает тенденцию;

Сделать точечный и интервальный прогноз выхода продукции по этому уравнению на ближайший год;

Для характеристики точности прогноза вычислить среднюю ошибку аппроксимации.

Сделать выводы.

Методика выполнения компьютерных расчетов

Нахождение параметров уравнений и построение графиков:

-Построить график с фактическими данными

Выделить столбец с исходными данными ----->Вставка----->Диаграмма----->График(с маркерами помечающими точки данных) ----->Далее (подписать название графика, оси координат) ----->Готово.

-Щелкнуть мышью в области диаграммы----->Диаграмма----->Добавить линию тренда-----> в появившемся диалоговом окне задать следующие параметры: -Тип----->выбрать нужное уравнение (например линейное), затем

-Параметры----->Установить флажок: -Показывать уравнение на диаграмме ----->ОК.

Аналогично постройте графики и осуществите нахождение параметров следующих уравнений: полинома 2 степени, полинома 3 степени, степенного, логарифмического, экспоненциального.

Нахождение выравненных уровней:

Уровни, выравненные по линейному уравнению определим следующим образом

( используется линейное уравнение из рассмотренного ниже примера): в ячейку D3 введем формулу выравненных уровней (=16,495+0,5214*C3).

Скопируем ячейку D3 в ячейки D4: D17.

Сглаженные уровни по логарифмической, степенной, экспоненциальной или полиноминальной линии тренда осуществляются аналогично выравниванию по линейной линии тренда.

Рассмотрим выполнение на примере

Суть аналитического выравнивания состоит в замене фактических (эмпирических) уровней теоретическими, вычисленными по какому – либо уравнению (линейному, степенному, логарифмическому и др.).

Для нахождения наиболее адекватного уравнения тренда используем инструмент «Подбор линии тренда» из мастера диаграмм Microsoft Excel. Результаты подбора приведем в таблице. Для наглядности представим фактический и выравненные уровни на графике 1.

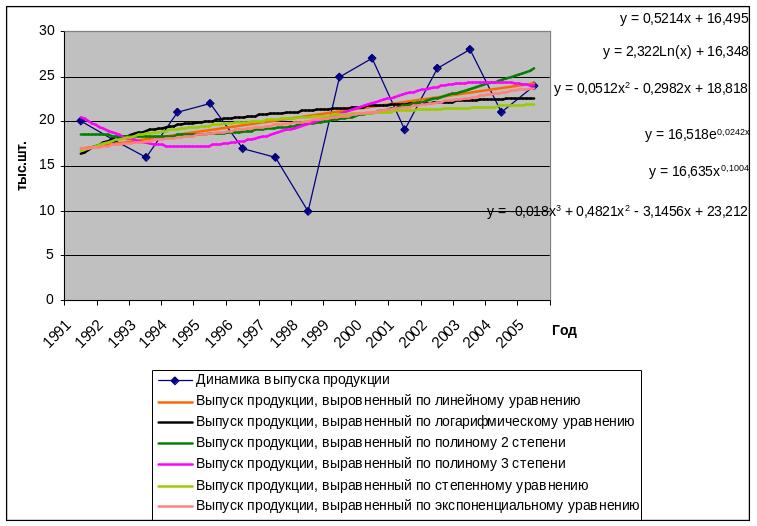
Рис.1 – Выпуск продукции фактический и выровненный по методу наименьших квадратов

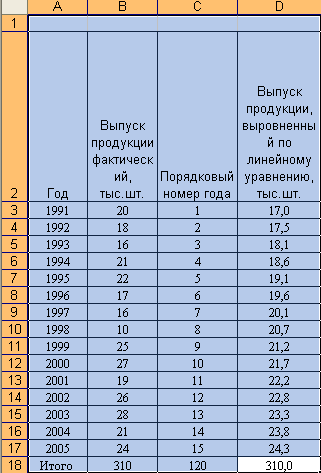
Вычислим выровненные уровни выпуска продукции, представим расчеты в таблице 1.

Таблица 1 – Выпуск продукции, выровненный по методу наименьших квадратов

Год	Выпуск продукции фактический, тыс.шт. У	Порядковый номер года	Выпуск продукции, выровненный по уравнению, тыс. шт.
			Линейно-му	Логарифмическому	Полиному 2 степени	Полиному 3 степени	Степен-ному	Экспонен-циальному
1	2	3	4	5	6	7	8	9
1991	20	1	17,0	16,3	18,6	20,5	16,6	16,9
1992	18	2	17,5	18,0	18,4	18,7	17,8	17,3
1993	16	3	18,1	18,9	18,4	17,6	18,6	17,8
1994	21	4	18,6	19,6	18,4	17,2	19,1	18,2
1995	22	5	19,1	20,1	18,6	17,3	19,6	18,6
1996	17	6	19,6	20,5	18,9	17,8	19,9	19,1
1997	16	7	20,1	20,9	19,2	18,6	20,2	19,6
1998	10	8	20,7	21,2	19,7	19,7	20,5	20,0
1999	25	9	21,2	21,4	20,3	20,8	20,7	20,5
2000	27	10	21,7	21,7	21,0	22,0	21,0	21,0
2001	19	11	22,2	21,9	21,7	23,0	21,2	21,5
2002	26	12	22,8	22,1	22,6	23,8	21,3	22,1
2003	28	13	23,3	22,3	23,6	24,2	21,5	22,6
2004	21	14	23,8	22,5	24,7	24,3	21,7	23,2
2005	24	15	24,3	22,6	25,9	23,8	21,8	23,7
Итого	310	120	310,0	310,0	310,0	309,3	301,6	302,2

/¹Суммы фактических и выравненных уровней должны совпадать. В данном случае наблюдается небольшая погрешность, что связано с проводимыми округлениями./

Таблица 2 – Уравнения выравнивания выпуска продукции по методу наименьших квадратов

Вид уравнения	Уравнение
Линейное
Полином 2 степени
Полином 3 степени
Логарифмическое
Степенное
Экспоненциальное

Наиболее точно отражает тенденцию то уравнение, при котором наблюдается наименьшее остаточное среднее квадратическое отклонение ( ). ,

где У – фактические уровни ряда динамики, - уровни, выровненные по какому – либо уравнению,

n – число лет, р – количество параметров уравнения.

Для расчета остаточных средних квадратических отклонений вычислим в начале квадраты отклонений (Таблица 3), затем сами остаточные квадратические отклонения (Таблица 4).

Можно вычислить также коэффициент случайной вариации по отношению к среднему уровню ряда ( ).

Таблица 3 – Квадраты отклонений фактических уровней от выравненных

Год	Квадрат отклонений фактических уровней от выравненных по уравнению
	линейному	логарифми- ческому	полиному 2 степени	полиному 3 степени	степенному	экспонен-циальному
1991	8,902	13,337	2,042	0,281	11,323	9,521
1992	0,214	0,002	0,182	0,497	0,028	0,451
1993	4,240	8,404	5,684	2,651	6,630	3,074
1994	5,853	2,054	6,531	14,507	3,537	7,907
1995	8,398	3,667	11,512	22,217	5,991	11,333
1996	6,882	12,309	3,504	0,650	8,489	4,368
1997	17,179	23,682	10,494	6,979	17,844	12,657
1998	113,768	124,913	94,269	93,811	110,190	100,736
1999	14,534	12,603	22,265	17,391	18,139	20,003
2000	27,995	28,147	36,530	25,341	36,463	35,637
2001	10,435	8,503	7,469	15,892	4,679	6,479
2002	10,551	15,070	11,476	4,914	21,634	15,419
2003	22,343	32,447	19,411	14,077	41,977	29,010
2004	7,810	2,178	13,531	10,714	0,465	4,700
2005	0,100	1,860	3,478	0,062	4,698	0,070
Итого	259,205	289,176	248,379	229,984	292,087	261,364

Вычислим остаточные средние квадратические отклонения (таблица 4).

Таблица 4 – Остаточные средние квадратические отклонения

Вид уравнения	Количество параметров уравнения, р	Сумма квадратов отклонений,	Остаточное среднее квадратическое отклонение,	Коэффициент случайной вариации, %
Линейное	2	259,205	4,47 = min	21,63
Полином 2 степени	3	248,379	4,55	22,01
Полином 3 степени	4	229,984	4,57	26,95
Логарифмическое	2	289,176	4,72	22,84
Степенное	2	292,087	4,74	22,93
Экспоненциальное	2	261,364	4,48	21,67

Как показали расчеты, наименьшее остаточное среднее квадратическое отклонение получилось при выравнивании по линейному уравнению. Следовательно, это уравнение наиболее точно отражает тенденцию изменения выпуска продукции.

Сделаем точечный прогноз выпуска продукции на 2006 год. Для этого в решенное линейное уравнение вместо Х подставим номер прогнозируемого года (16) получим:

= 0,5214 ∙ 16 + 16,495 = 24,84 тыс. шт.

Таким образом, ожидаемый выпуск продукции в 2006 году составит 24,84 тыс. шт..

Прогноз должен иметь вероятностный характер, как любое суждение о будущем. Для этого вычисляется средняя ошибка прогноза положения тренда на прогнозируемый год с номером t_k, обозначаемая

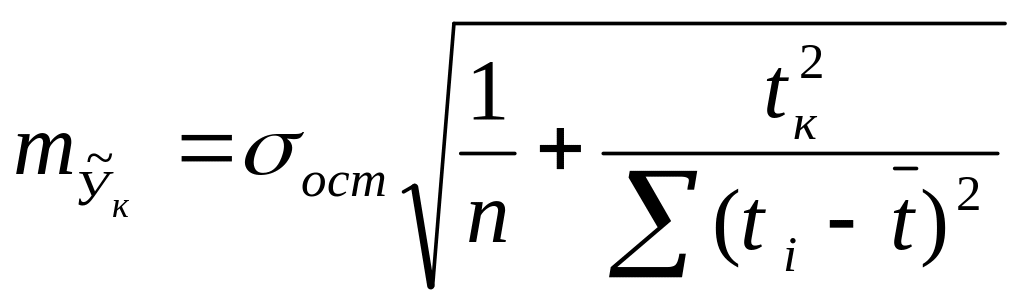
где n – число уровней исходного ряда – базы прогноза,

Вычислим среднюю ошибку прогноза на 2006 год (t=16).

Для вычисления доверительного интервала прогноза положения тренда среднюю ошибку необходимо умножить на величину t –критерия Стьюдента при имеющемся числе степеней свободы колебаний (15-2=13) и при выбранной вероятности (надежности прогноза). Для вероятности 0,95 t – критерий Стьюдента = 2,16.

/ ¹ Таблица для определения t – Стьюдента приведена в Приложении. /

Следовательно, доверительный интервал прогноза положения тренда на 2006 г. составит:

24,84 ± 2,16 ∙ 4,42 = 24,84 ± 9,55 тыс. шт.

Таким образом, с вероятностью 0,95 можно предположить, что в 2006 году на предприятии выпуск продукции будет находиться в пределах от 15,29 до 34,39 тыс. шт.

В качестве характеристики точности прогноза на практике определяют среднюю ошибку аппроксимации, которая выражается в процентах относительно фактических значений признака, и определяется по формуле:

Данный показатель является относительным показателем точности прогноза.

Таблица 5 - Интерпретация точности прогноза

, %	Интерпретация точности
< 10 10 – 20 20 – 50 > 50	Высокая Хорошая Удовлетворительная Не удовлетворительная

Вычислим среднюю ошибку аппроксимации:

Следовательно, точность прогноза – хорошая.