10.2.7. Інваріантність форми повного диференціала

Використовуючи правило диференціювання складної функції, можна показати, що повний диференціал володіє властивістю інваріантності: повний диференціал функції зберігає один і той же вигляд незалежно від того, чи є аргументи незалежними змінними або функціями незалежних змінних.

Нехай , де і – незалежні змінні. Тоді повний диференціал (1-го порядку) функції має вигляд

(формула (2.5)).

Розглянемо складну функцію , де , , тобто функцію , де і - незалежні змінні. Тоді маємо:

Вирази в дужках представляють собою повні диференціали і функцій і . Отже, і в цьому випадку

10.2.8. Диференціювання неявної функції

Функція називається неявною, якщо вона задається рівнянням

(2.11)

нерозв’язним щодо . Знайдемо частинні похідні і неявної функції , заданої рівнянням (2.11). Для цього, підставивши в рівняння замість функцію , отримаємо тотожність Частинні похідні по і по функції, тотожно рівній нулю, також рівні нулю:

( – вважаємо сталою)

( – вважаємо сталою)

звідки 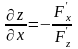і

Зауваження.

а) Рівняння вигляду (2.11) не завжди визначає одну змінну як неявну функцію двох інших. Так, рівняння визначає функції або , визначені в крузі , визначену в півколі при і т. д., а рівняння не визначає ніякої функції.

Має місце теорема існування неявної функції двох змінних:

Якщо функція і її похідні визначені і безперервні в деякій околі точки , причому , a , то існує окіл точки , в якій рівняння (2.11) визначає єдину функцію , неперервну і диференційовну в околі точки і таку, що .

б) Неявна функція однієї змінної задається рівнянням . Можна показати, що у випадку, якщо виконуються умови існування неявної функції однієї змінної (є теорема, аналогічна вищезгаданій), то похідна неявної функції знаходиться по формулі

(2.12)

Приклад 6. Знайти частинні похідні функції , заданої рівнянням .

 Тут

По формулах (2.12) маємо : 

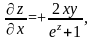
Приклад 7. Знайти 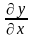, якщо неявна функція задана рівнянням

 Тут Отже

тобто 

10.3. Дотична площина і нормаль до поверхні

Р озглянемо одне геометричне застосування частинних похідних функції двох змінних. Нехай функція диференційовна в точці деякої області. Перетнемо поверхню , що зображає функцію , площинами і (див. рис. 4). Площина перетинає поверхню по деякій лінії , рівняння якої виходить підстановкою у вираз початкової функції замість числа . Точка належить кривій. Через диференційовність функції в точці функція також диференціюється в точці . Тому, в цій точці площини до кривої може бути проведена дотична пряма .

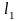Рис.4

Проводячи аналогічні міркування для перетину , побудуємо дотичну пряму до кривої в точці . Прямі і визначають площину, яка називається дотичною площиною до поверхні в точці .

Складемо її рівняння. Оскільки площина проходить через точку , то її рівняння може бути записано у вигляді

яке можна переписати так:

(3.1)

(розділивши рівняння на і позначивши ).

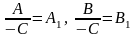Знайдемо і : Рівняння дотичних і мають вигляд

відповідно.

Дотична лежить в площині , отже, координати всіх точок задовольняють рівняння (3.1). Цей факт можна записати у вигляді системи

Розв’язуючи цю систему відносно , отримаємо, що Проводячи аналогічні міркування для дотичної , легко встановити, що

Підставивши значення і в рівняння (3.1), одержуємо шукане рівняння дотичної площини:

(3.2)

Пряма, що проходить через точку і перпендикулярна дотичній площини, побудованої в цій точці поверхні, називається її нормаллю.

Використовуючи умову перпендикулярності прямої і площини (див. з. 87), легко отримати канонічні рівняння нормалі:

(3.3)

Якщо поверхня задана рівнянням , то рівняння (3.2) і (3.3), з урахуванням того, що частинні похідні можуть бути знайдені як похідні неявної функції:

(див. формули (2.12)), приймуть відповідно вигляд

і

Зауваження. Формули дотичної площини і нормалі до поверхні отримані для звичайних, тобто не особливих, точок поверхні. Точка поверхні називається особливою, якщо в цій точці всі частинні похідні рівні нулю або хоча б одна з них не існує. Такі точки ми не розглядаємо.

Приклад 1. Написати рівняння дотичної площини і нормалі до параболоїда обертання в точці .

Тут, , ,

Користуючись формулами (3.2) і (3.3) одержуємо рівняння дотичної площини:

або і рівняння нормалі:

