10.1.2. Границя функції

Д ля функції двох (і більшого числа) змінних вводиться поняття границі функції і неперервності, аналогічно випадку функції однієї змінної. Введемо поняття околу точки. Множина всіх точок площини, координати яких задовольняють нерівності 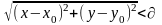називається – околом точки . Іншими словами, -окіл точки - це всі внутрішні точки круга з центром і радіусом (див. рис. 2).

Рис. 2

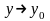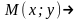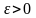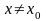Нехай функція визначена в деякому околі точки окрім, можливо, самої цієї точки . Число називається границею функції при при (або, що те ж саме, при ), якщо для будь-якого існує таке , що для всіх і задовольняють нерівність виконується нерівність 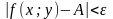. Записують: або

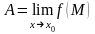
З визначення витікає, що якщо границя існує, то вона не залежить від шляху, по якому прямує до (число таких напрямів нескінченне; для функції однієї змінної по двох напрямах: справа і зліва!)

Геометричний зміст границі функції двох змінних полягає в наступному. Яке б не було число , знайдеться - окіл точки , що у всіх її точках , відмінних від аплікати відповідних точок поверхні відрізняються від числа по модулю менше ніж на .

Приклад 1. Знайти границю .

 Будемо наближатися до по прямій 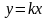, де – деяке число. Тоді

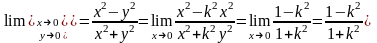
Функція 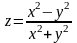в точці границі не має, так як при різних значеннях границя функції не однакова (функція має різні граничні значення).

Границя функції двох змінних володіє властивостями, аналогічними властивостям границі функції однієї змінної (див. п. 17.3). Це означає, що справедливі твердження: якщо функції і 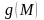визначені на множині і мають в точці цієї множини межі і 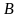відповідно, то і функції , 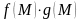, мають в точці границі, які відповідно рівні , , .

10.1.3. Неперервність функції двох змінних

Функція (або ) називається неперервною в точці 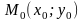, якщо вона:

а) визначена в цій точці і деякому її околі;

б) має границю _;

в) ця границя рівна значенню функції в точці , тобто

або .

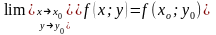Функція, неперервна в кожній точці деякої області, називається неперервною в цій області. Точки, в яких неперервність порушується (не виконується хоча б одна з умов неперервності функції в точці), називаються точками розриву цієї функції. Точки розриву можуть утворювати цілі лінії розриву. Так, функція має лінію розриву .

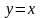Можна дати інше, рівносильне приведеному вище, визначення неперервності функції в точці. Позначимо , , .

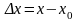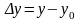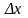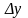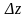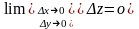Величини і називаються приростами аргументів і , а – повним приростом функції в точці . Функція називається неперервною в точці якщо виконується рівність , тобто повний приріст функції в цій точці прямує до нуля, коли прирости її аргументів і прямують до нуля.

Користуючись визначенням неперервності і теоремами про границі, можна довести, що арифметичні операції над неперервними функціями і побудова складної функції з неперервних функцій приводить до неперервних функцій – подібні теореми мали місце для функцій однієї змінної (див. п. 19.4).