
- •Функції багатьох змінних
- •Тема 10.1. Функції двох змінних.
- •Тема 10.2. Похідні і диференціали функцій декількох змінних.
- •Тема 10.3. Дотична площина і нормаль до поверхні.
- •Тема 10.4. Екстремум функції двох змінних.
- •10.4.1. Основні поняття.
- •10.1. Функції двох змінних
- •10.1.1. Основні поняття
- •10.1.2. Границя функції
- •10.1.3. Неперервність функції двох змінних
- •10.1.4. Властивості функцій, неперервних в обмеженій замкненій області
- •10.2. Похідні і диференціали функцій декількох змінних
- •10.2.1. Частинні похідні першого порядку та їх геометричний зміст
- •Геометричний зміст частинних похідних функції двох змінних
- •10.2.2. Частинні похідні вищих порядків
- •10.2.3. Диференційовність і повний диференціал функції.
- •10.2.4. Застосування повного диференціала для наближених обчислень
- •10.2.5. Диференціали вищих порядків
- •10.2.6. Похідна складної функції. Повна похідна
- •10.2.7. Інваріантність форми повного диференціала
- •10.2.8. Диференціювання неявної функції
- •10.3. Дотична площина і нормаль до поверхні
- •10.4. Екстремум функції двох змінних
- •10.4.1. Основні поняття
- •10.4.2. Необхідні і достатні умови екстремуму
- •10.4.3. Найбільше і найменше значення функції в замкнутій області
10.2.2. Частинні похідні вищих порядків
Частинні
похідні
 и
и
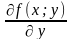 називають частинними
похідними першого порядку.
Їх можна розглядати як функції від
називають частинними
похідними першого порядку.
Їх можна розглядати як функції від
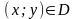 . Ці функції можуть мати частинні похідні,
які називаються частинними
похідними другого порядку.
Вони визначаються і позначаються таким
чином:
. Ці функції можуть мати частинні похідні,
які називаються частинними
похідними другого порядку.
Вони визначаються і позначаються таким
чином:
 ;
;
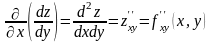 ;
;
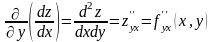 ;
;
 .
.
Аналогічно визначаються частинні похідні 3-го, 4-го і т. д. порядків.
Так
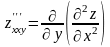 ,
,
Частинна
похідна другого або більш високого
порядку, узята по різних змінних,
називається змішаною
частинною похідною
. Такими є, наприклад
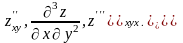
Приклад 2. Знайти частинні похідні другого порядку функції

Оскільки
 і
і
 ,
то
,
то
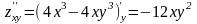 .
Виявилося,
що
.
Виявилося,
що
 .
.
Цей результат не випадковий. Має місце теорема, яку наведемо без доведення.
Теорема
10.2.1
(Шварца). Якщо частинні похідні вищого
порядку неперервні, то змішані похідні
одного порядку, відмінні лише порядком
диференціювання, рівні між собою.
Зокрема, для
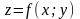 маємо:
маємо:
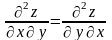 .
.
10.2.3. Диференційовність і повний диференціал функції.
Нехай
функція
визначена
в деякому околі точки
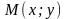 .
Складемо повний приріст функції в точці
:
.
Складемо повний приріст функції в точці
:
Функція називається диференційовною в точці , якщо її повний приріст в цій точці можна представити у вигляді
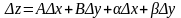 ,
(2.1)
,
(2.1)
де
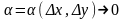 і
і
 при
при
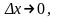

Сума перших двох доданків в рівності (2.1) представляє собою головну частину приросту функції.
Головна
частина приросту функції
,
лінійна відносно
і
називається повним
диференціалом
цієї функції і позначається символом
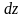 :
:
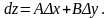 (2.2)
(2.2)
Вирази
 и
и
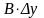 називають частинними
диференціалами.
Для незалежних змінних
і
вважають
називають частинними
диференціалами.
Для незалежних змінних
і
вважають
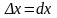 і
і
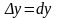 .
Тому рівність (2.2)
можна переписати у вигляді
.
Тому рівність (2.2)
можна переписати у вигляді
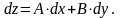 (2.3)
(2.3)
Теорема
10.2.2
(необхідна умова диференційовності
функції). Якщо функція
диференційовна
в точці
,
то вона неперервна в цій точці, має в
ній частинні похідні
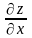 і
і
 причому
причому
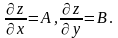
Оскільки
функція диференційовна в точці
,
то має місце рівність (2.1).
Звідси випливає, що
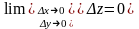 . Це означає, що функція неперервна в
точці
.
Поклавши
. Це означає, що функція неперервна в
точці
.
Поклавши
 в рівності (2.1),
отримаємо:
в рівності (2.1),
отримаємо:
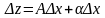 .
Звідси знаходимо
.
Звідси знаходимо
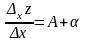 . Переходячи до межі
. Переходячи до межі
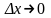 при
,
отримаємо
при
,
отримаємо
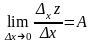 ,
тобто
,
тобто
 .
Таким чином, в точці
існує частинна похідна
.
Таким чином, в точці
існує частинна похідна
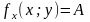 .
Аналогічно доводиться, що в точці
існує частинна похідна
.
Аналогічно доводиться, що в точці
існує частинна похідна
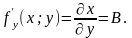
Рівність (2.1) можна записати у вигляді
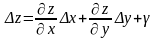 (2.4)
(2.4)
де
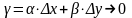 при
при

Відзначимо,
що зворотне твердження хибне, тобто з
неперервності функції, або існування
частинних похідних не слідує
диференційовність функції. Так, неперервна
функція
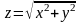 не диференційовна в точці
не диференційовна в точці
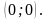
Як наслідок теореми одержуємо формулу для обчислення повного диференціала. Формула (2.3) приймає вигляд:
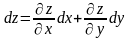 або
або
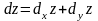 ,
(2.5)
,
(2.5)
де
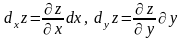 −
частинні диференціали функції
.
−
частинні диференціали функції
.
Теорема
10.2.3
(достатня
умова диференційовності функції). Якщо
функція
має неперервні частинні похідні
 і
і
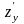 в точці
,
то вона диференційовна в цій точці і її
повний диференціал виражається формулою
(2.5).
в точці
,
то вона диференційовна в цій точці і її
повний диференціал виражається формулою
(2.5).
Приймемо
теорему без доведення.
Відзначимо,
що для функції
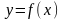 однієї змінної існування
похідної
однієї змінної існування
похідної
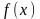 в
точці є необхідною і достатньою умовою
її
диференційовності в цій точці.
в
точці є необхідною і достатньою умовою
її
диференційовності в цій точці.
Щоб функція була диференційовна в точці, необхідно, щоб вона мала в ній частинні похідні, і достатньо, щоб вона мала в точці неперервні частинні похідні.
Арифметичні властивості і правила знаходження диференціалів функції однієї змінної зберігаються і для диференціалів функції двох (і більшого числа) змінних.
