
- •Поліном Лагранжа
- •Завдання для самостійної роботи
- •Тема: Апроксимація функцій Теоретичні відомості Емпіричні формули
- •Визначення параметрів емпіричної залежності
- •Метод найменших квадратів
- •Розв’язок
- •Завдання для самостійної роботи
- •Розв’язок
- •Метод Сімпсона
- •Розв’язок
- •Завдання для самостійної роботи
- •Лабораторна рОбота №3
- •Теоретичні відомості Чисельне розв’язання систем лінійних алгебраїчних рівнянь
- •Метод Гаусса
- •Метод Гаусса-Зейделя
- •Розв’язок
- •Завдання для самостійної роботи
- •Лабораторна рОбота №4 Тема: Нелінійні рівняння Теоретичні відомості
- •Метод хорд
- •Метод Ньютона (метод дотичних)
- •Розв’язок
- •Комбінований метод хорд і дотичних
- •Метод ітерацій або метод послідовних наближень
- •Розв’язок
- •Завдання для самостійної роботи
- •Лабораторна рОбота №5 Тема: Чисельне розв’язання звичайних диференційних рівнянь Теоретичні відомості
- •Метод Ейлера
- •Модифікації методу Ейлера
- •Метод Рунге-Кутта
- •Завдання для самостійної роботи
- •Список літератури
Метод хорд
Ідея
методу хорд полягає в тому, що на достатньо
малому проміжку
![]() дуга кривої
дуга кривої
![]() заміняється стягуючою її хордою. Шуканий
корінь рівняння
заміняється стягуючою її хордою. Шуканий
корінь рівняння
![]() є абсциса точки перетину графіка функції
з віссю Ох.
Ця точка нам невідома, але замість її
ми візьмемо точку
є абсциса точки перетину графіка функції
з віссю Ох.
Ця точка нам невідома, але замість її
ми візьмемо точку
![]() перетину хорди АВ
із віссю Ох.
перетину хорди АВ
із віссю Ох.
Розглянемо
випадок, коли перша і друга похідні
мають однакові знаки, тобто
![]() (рис.1).
Як нульове наближення кореня в даному
випадку приймається ліва межа інтервалу
ізольованого кореня, тобто
(рис.1).
Як нульове наближення кореня в даному
випадку приймається ліва межа інтервалу
ізольованого кореня, тобто
![]() .
.
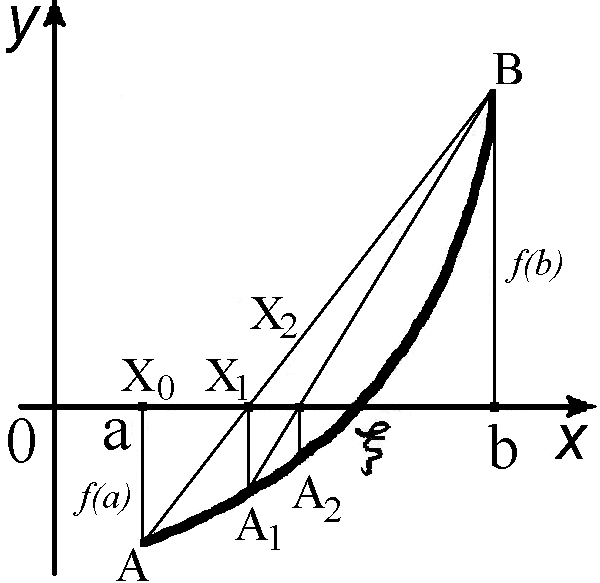
Рисунок
1 – Метод хорд, у випадку коли
![]() мають
однакові знаки
мають
однакові знаки
Перше, друге і інші наближення кореня знаходяться з формули, яка витікає з рівняння хорди. Рівняння хорди АВ записується як рівняння прямої, яка проходить через дві крапки з відомими координатами:
|
(2) |
Значення
![]() ,
для якого
,
для якого
![]() ,
тобто точка перетину хорди з віссю
абсцис розташовується ближче до точного
значення кореня, ніж
і визначається з виразу:
,
тобто точка перетину хорди з віссю
абсцис розташовується ближче до точного
значення кореня, ніж
і визначається з виразу:
|
(3) |
Обчислимо значення
![]() .
Геометрично
– довжина перпендикуляра до осі Ох,
проведеного з точки до кривої
.
Геометрично
– довжина перпендикуляра до осі Ох,
проведеного з точки до кривої
![]() .
Якщо
.
Якщо
![]() ,
то знайдено більш вузький інтервал
існування кореня
,
то знайдено більш вузький інтервал
існування кореня
![]() ,
оскільки знаки
,
оскільки знаки
![]() і
і
![]() збігаються. Тепер корінь знаходиться
у середині відрізка
.
Якщо значення кореня
не влаштовує, то його можна уточнити,
застосовуючи метод хорд до відрізка
,
тобто побудувавши хорду А1В,
записавши її рівняння і визначаючи
точку перетину
збігаються. Тепер корінь знаходиться
у середині відрізка
.
Якщо значення кореня
не влаштовує, то його можна уточнити,
застосовуючи метод хорд до відрізка
,
тобто побудувавши хорду А1В,
записавши її рівняння і визначаючи
точку перетину
![]() хорди А1В із віссю абсцис:
хорди А1В із віссю абсцис:
|
(4) |
та інше.
1. Якщо мають місце
варіанти I і II, тоді
![]() на відрізку
,
то наближені значення корінів
на відрізку
,
то наближені значення корінів
![]() знаходитимуться усередині відрізків
,
знаходитимуться усередині відрізків
,
![]() ,
,
…, тобто нерухомим кінцем відрізка
буде кінець
,
а наближені значення коренів будуть
знаходитися за формулою:
,
,
…, тобто нерухомим кінцем відрізка
буде кінець
,
а наближені значення коренів будуть
знаходитися за формулою:
|
(5) |
при
цьому
![]() (рис. 1).
(рис. 1).
2. Якщо мають місце
варіанти III і IV, тоді
![]() на відрізку
,
то наближені значення
коренів будуть знаходитися усередині
відрізків
на відрізку
,
то наближені значення
коренів будуть знаходитися усередині
відрізків
![]() ,
,
![]() ,
…, тобто нерухомим кінцем відрізка
буде кінець
,
а наближені значення коренів будуть
знаходитися за формулою:
,
…, тобто нерухомим кінцем відрізка
буде кінець
,
а наближені значення коренів будуть
знаходитися за формулою:
|
(6) |
при
цьому
![]() (рис. 2).
(рис. 2).
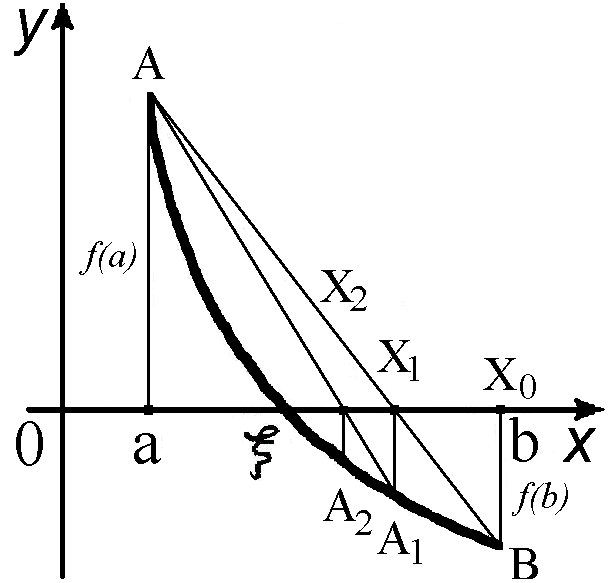
Рисунок 2 – Метод хорд, у випадку коли мають різні знаки
Вибір тих або інших формул можна здійснити, користуючись простим правилом: нерухомим кінцем відрізку є той, для якого знак функції співпадає із знаком другої похідної, а нульове наближення обирається відповідно до умови:
|
(7) |
Процес
послідовного наближення до корня слід
продовжувати доти, поки не буде виконана
умова
![]() ,
де
‑ задана точність;
,
де
‑ задана точність;
![]() і
і
![]() – наближення, отримані на
-му
але
– наближення, отримані на
-му
але
![]() -му
кроках. При цьому уточнене значення
кореня приймається рівним
-му
кроках. При цьому уточнене значення
кореня приймається рівним
![]() .
.
Метод Ньютона (метод дотичних)
Геометрично
метод Ньютона еквівалентний
заміні невеликої дуги кривої
![]() дотичною, проведеною до деякої точки
кривої, наприклад, крапки В
(рис. 3).
Точка перетину цієї дотичної з віссю
абсцис дає перше наближення
дотичною, проведеною до деякої точки
кривої, наприклад, крапки В
(рис. 3).
Точка перетину цієї дотичної з віссю
абсцис дає перше наближення
![]() кореня
.
кореня
.
Рівняння дотичної до кривої в крапці В має наступний вид:
|
(8) |
Вважаючи, що , знаходимо абсцису точки перетину цієї дотичної з віссю Ох:
|
(9) |
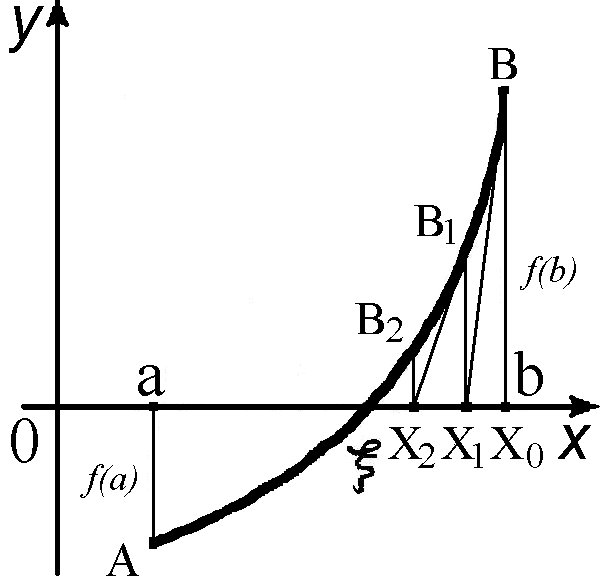
Рисунок 3 – Ілюстрація методу Ньютона
Значення приймаємо як перше наближення кореня . У крапці визначаємо значення функції . Геометрично це довжина перпендикуляра до осі Ох, відновленого в до його перетину з кривою у точці В1.
Процес продовжується
таким чином: проведемо дотичну до точки
В1 і знайдемо точку перетину цієї
дотичної з віссю абсцис
.
Крапку
приймаємо як друге наближення кореня
.
Процес продовжується до тих пір, поки
не буде одержане значення кореня із
заданим ступенем точності. Будь-яке
![]() -ше
наближення кореня визначається рівністю:
-ше
наближення кореня визначається рівністю:
|
(10) |
Вибір
нульового наближення кореня
![]() здійснюється таким чином:
здійснюється таким чином:
якщо
![]() на
,
то
;
на
,
то
;
якщо
![]() на
,
то
.
на
,
то
.
Чим
більше чисельне значення похідної
![]() в околі даного кореня, тим менша поправка,
яку необхідно враховувати в
-му
наближенні. Тому метод Ньютона особливо
зручно застосовувати тоді, коли в околі
даного кореня графік функції має велику
крутизну.
в околі даного кореня, тим менша поправка,
яку необхідно враховувати в
-му
наближенні. Тому метод Ньютона особливо
зручно застосовувати тоді, коли в околі
даного кореня графік функції має велику
крутизну.
Якщо чисельне значення похідної біля кореня мале, то поправки будуть великими і процес уточнення кореня може виявитися тривалим. Якщо крива поблизу точки перетину з віссю Ох майже горизонтальна, то застосовувати метод Ньютона не рекомендується.
Точність
наближення на
-му
кроці оцінюється таким чином: якщо
,
то
![]() .
.
Якщо похідна мало змінюється на відрізку , то для спрощення обчислень можна використовувати формулу:
|
(11) |
тобто
значення похідної в початковій точці
достатньо обчислити один раз. Геометрично
це означає, що дотичні в точках
![]() замінюються прямими, паралельними
дотичній, яка проведена до кривої
у точці
замінюються прямими, паралельними
дотичній, яка проведена до кривої
у точці
![]() (рис. 3).
(рис. 3).
Приклад.
Методом
дотичних уточнити до
![]() корінь
рівняння
корінь
рівняння
![]() ,
який розташований на відрізку [-2.75;
-2.5].
,
який розташований на відрізку [-2.75;
-2.5].
