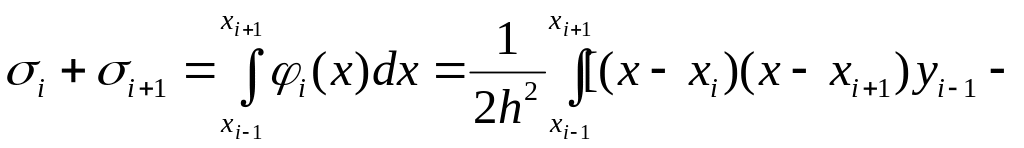Розв’язок

Цей інтеграл легко обчислюється за формулою Ньютона-Лейбниця:

.

Для обчислення даного інтеграла використаємо формули прямокутників і трапецій. Розіб'ємо відрізок інтегрування [0,1] на десять рівних частин: , . Обчислимо значення підінтегральної функції у точках розбиття , а також в напівцілих точках ( ) (табл. 1).

Таблиця 1

0 1 2 3 4 5 6 7 8 9 10	0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0	1,000000 0,990099 0,961538 0,917431 0,862069 0,800000 0,735294 0,671141 0,609756 0,552486 0,500000	0,05 0,15 0,25 0,35 0,45 0,55 0,65 0,75 0,85 0,95	0,997506 0,977995 0,941176 0,890868 0,831601 0,767754 0,702988 0,640000 0,580552 0,525624

По формулі прямокутників (5) отримаємо:

.

Похибка в обчисленні інтеграла складає (близько 0.027 %). Використовуючи формулу трапецій (6), знаходимо:

.

Похибка тут дорівнює (близько 0.054 %).

Таким чином, в розглянутому прикладі кращу точність обчислення інтеграла дає формула прямокутників. Це, на перший погляд, несподіваний результат, оскільки формула прямокутників використовує інтерполяцію нульового порядку (кусочно-постійну), тоді як формула трапецій використовує кусочно-лінійну інтерполяцію. Підвищення точності тут пояснюється способом обчислення елементарних площ що використовує значення функції в центральній точці відрізку [ ]. Відмітимо, що використання формул прямокутників у вигляді (1) або (2) приведе до похибки більше 3 %.

Похибка чисельного інтегрування визначається кроком розбиття. Зменшуючи цей крок, можна добитися більшої точності. Правда, збільшувати число точок не завжди можливо. Якщо функція задана в табличному вигляді, доводиться, як правило, обмежуватися даною кількістю точок. Підвищення точності в цьому випадку може бути досягнуте за рахунок підвищення ступеня використовуваних інтерполяційних багаточленів. Розглянемо один з таких способів чисельного інтегрування: використання квадратичної інтерполяції (метод Сімпсона).

Метод Сімпсона

Розіб'ємо відрізок інтегрування на парне число рівних частин з кроком . На кожному відрізку [ ], [ ],...,[ ], ...,[ ] підінтегральну функцію замінимо інтерполяційним поліномом другого ступеня:

, .

Коефіцієнти цього поліному можуть бути знайдені з умов рівності багаточлена в точках відповідним табличним даним . У якості можна прийняти інтерполяційний багаточлен Лагранжа другого ступеню, що проходить через крапки , , :

.

Сума елементарних площ и (рис. 2) може бути підрахована за допомогою визначеного інтеграла. Враховуючи рівності , отримуємо:

.

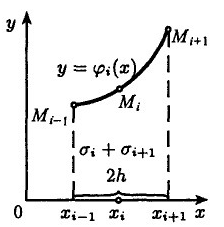
Рисунок 2 – Сума елементарних площ і

Провівши такі обчислення для кожного елементарного відрізку [ ], підсумуємо отримані вирази:

.

Останній вираз для приймається як значення визначеного інтеграла:

.

(7)

Отримане співвідношення називається формулою Сімпсона або формулою парабол.

Іноді формулу Сімпсона записують із застосуванням напівцілих індексів. В цьому випадку число відрізків розбиття довільне (не обов'язково парне), і формула Сімпсона має вид:

.

(8)

Легко побачити, що формула (8) співпаде з (7), якщо формулу (7) застосувати для числа відрізків розбиття і кроку .

Приклад.

Обчислити за методом Сімпсона інтеграл .