Файловый архив студентов. Файловый архив студентов.
1301 вуз, 5089 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Украинский Государственный химико-технологический Университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
Чисельні методи.doc
Скачиваний:
15
Добавлен:
28.08.2019
Размер:
9.78 Mб
Скачать
☆
►Содержание►

Розв’язок

Якщо зобразити задані табличні значення на графіці (рис. 1), то легко переконатися, що в якості емпіричної формули для апроксимації функції можна прийняти поліном другого ступеню, графіком якого є парабола:

.

В даному випадку маємо:

, , , , ,

, , .

Після обчислення матриці і вектора маємо:

, .

Система рівнянь (16) приймає наступний вид:

.

Звідки знаходимо значення параметрів емпіричної формули: , , . Таким чином, отримуємо наступну апроксимацію функції, заданої у табличному виді:

.

Оцінимо відносні похибки отриманої апроксимації в заданих точках, тобто знайдемо значення .

Результати обчислень представимо у виді таблиці 2:

Таблиця 2

0,75

1,50

2,25

3,00

3,75

2,47

1,25

1,15

2,17

4,32

2,50

1,20

1,12

2,25

4,28

-0,03

0,05

0,03

-0,08

0,04

-0,012

0,042

0,027

-0,036

0,009

На рис. 1 побудовано графік знайденої емпіричної функції. Крапками, нанесені задані табличні значення функції .

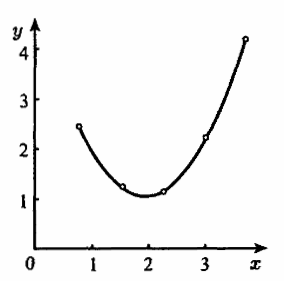
Рисунок 1 – Графік емпіричної функції

Завдання для самостійної роботи

Використовуючи метод найменших квадратів вивести емпіричну формулу для функції , яка задана в табличному виді.

Таблиця 1

Таблиця 2

Таблиця 3

Таблиця 4

Таблиця 5

X

Y

0

54,8

2

24,1

4

7,5

7

13,8

9

35,1

10

55,1

X

Y

0,5

45,3

1,7

24,8

3,5

9,9

4,5

5,7

7,5

16,1

8,5

32,1

X

Y

-6

64,9

-5

50,2

1

4,6

3

3,5

4

7,9

6

19,7

X

Y

-4,5

43,6

-3,6

31,9

-1,8

17,8

0

7,1

5

11,3

7,5

32,7

X

Y

-10

-115,7

-8

-75,5

-7

-63,8

-2

-5,4

0

-1,2

1

2,9

Таблиця 6

Таблиця 7

Таблиця 8

Таблиця 9

Таблиця 10

X

Y

-3,5

15,9

-1,8

-4,4

-0,9

-2,2

0,2

1,7

0,9

3,9

2

5,3

X

Y

-4

-25,1

-2

-11,9

0

-3,2

1

-1,5

2

-3,2

3

-7,1

X

Y

3

-7,5

4

-11,6

5

-20,2

6

-29,9

7

-40,5

10

-82,3

X

Y

-7,5

-73,9

-6,8

-60,9

-5,5

-46,8

-3,9

-25,1

-2,2

-11,6

0

-3,2

X

Y

-5

-5,6

-4

-1,2

-3

2,1

2

-12,7

3

-21,7

4

-33,1

Таблиця 11

Таблиця 12

Таблиця 13

Таблиця 14

Таблиця 15

X

Y

-1,5

2,6

-0,5

0,5

0,5

-3,3

2,5

-17,4

3,5

-28,2

4,5

-39,7

X

Y

0

-1,1

1

-6,5

2

-12,7

3

-21,7

4

-33,2

5

-45,7

X

Y

-1

-2,1

-2

2,9

0

5,1

6

18,8

7

30,2

8

43,2

X

Y

-7

58,1

3

9,9

-1

-2,1

0

-5,2

1

-6,1

5

9,8

X

Y

-4,5

24,2

-3,5

14,2

0

-5,1

0,8

-5,9

1,5

-5,7

2,5

-3,7

Таблиця 16

Таблиця 17

Таблиця 18

Таблиця 19

Таблиця 20

X

Y

0

4,2

1

9,1

2

17,7

3

31,3

4

48,2

5

68,9

X

Y

-5

39,1

-3

12,8

-1

3,2

0

3,9

1

9,1

2

18,7

X

Y

-4,5

31,2

-3,8

21,4

-1,6

4,5

-0,7

2,7

0,3

5,2

1,2

10,6

X

Y

-5

-64,1

-3

-25,9

-1

-4,1

0

1,1

1

1,9

2

-1,1

X

Y

0

0,9

1

2,1

2

-1,1

3

-8,1

4

-18,8

5

-34,2

Таблиця 21

Таблиця 22

Таблиця 23

Таблиця 24

Таблиця 25

X

Y

-6,5

-103,2

-3,5

-34,1

-1,5

-7,8

-0,5

-1,2

0,5

2,1

1,5

0,8

X

Y

0

-5,1

2

-18,1

4

-48,8

6

-95,1

7

-124,3

9

-193,7

X

Y

-7

-82,2

-3

-14,4

6

-95,1

7

-124,1

8

-156,8

9

-194,3

X

Y

-6,5

-70,1

-3,5

-19,2

-1,5

-4,8

-0,5

-4,1

0,5

-7,1

1,5

-19,8

X

Y

0

-2,1

2

-3,8

4

2,2

6

16,3

7

26,1

8

37,8

Таблиця 26

Таблиця 27

Таблиця 28

Таблиця 29

Таблиця 30

X

Y

-7

68,2

-3

16,1

-1

2,2

0

-1,8

1

-4,2

5

8,1

X

Y

-6,5

59,9

-3,5

20,5

-1,5

4,8

-0,5

-0,3

0,5

-3,4

1,5

-4,4

X

Y

-5

16,6

-4

11,8

-3

8,5

2

24,1

3

32,9

4

44,5

X

Y

-1,5

8,1

-0,5

10,2

0,5

14,6

2,5

28,7

3,5

38,4

4,5

49,9

X

Y

0

12,2

1

17,1

2

24,1

3

32,9

4

44,5

5

57,1

Лабораторна рОбота №2

Тема: Чисельне інтегрування

Теоретичні відомості

Методи прямокутників і трапецій

Простим методом чисельного інтегрування є метод прямокутників. Він безпосередньо використовує заміну певного інтеграла інтегральною сумою:

.

У якості точок можуть вибиратися ліві ( ) або праві ( ) межі елементарних відрізків. Позначаючи , , отримуємо наступні формули метода прямокутників відповідно для цих двох випадків:

.

(1)

.

(2)

Більш поширеною та точнішою є формула прямокутників, що використовує значення функції в середніх точках елементарних відрізків (у напівцілих вузлах):

,

, .

(3)

Надалі під методом прямокутників розумітимемо останній алгоритм (він ще називається методом середніх).

У розглянутому методі прямокутників використовується кусочно-постійна інтерполяція: на кожному елементарному відрізку функція наближається функцією, що приймає постійні значення (константи). При цьому площа всієї фігури (криволінійної трапеції) приблизно складається з площ елементарних прямокутників. На рис. 1 верхня, середня і нижня горизонтальні штрихові лінії відносяться до елементарних прямокутників, які відповідають формулам (2), (3) і (1).

Метод трапецій використовує лінійну інтерполяцію, тобто графік функції представляється у вигляді ламаної такої, що сполучає точки ( ). В цьому випадку площа всієї фігури приблизно складається з площ елементарних прямолінійних трапецій (рис. 1). Площа кожної такої трапеції дорівнює добутку напівсуми основи на висоту:

.

Складаючи всі ці рівності, отримуємо формулу трапецій для чисельного інтегрування:

.

(4)

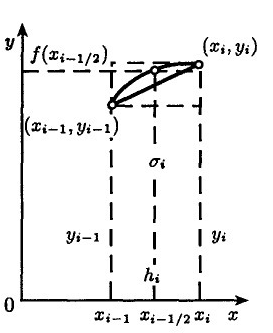
Рисунок 1 – Обчислення у методах прямокутників і трапецій

Важливим окремим випадком розглянутих формул є їх застосування при чисельному інтегруванні з постійним кроком ( ). Формули прямокутників і трапецій в цьому випадку приймають відповідно вид:

(5)

.

(6)

Розглянемо приклад використання цих формул при ручному підрахунку для простого інтеграла, що допускає також безпосереднє обчислення. Такий приклад дозволить порівняти результати розрахунків, отримані різними способами.

Приклад.

Обчислити інтеграл .

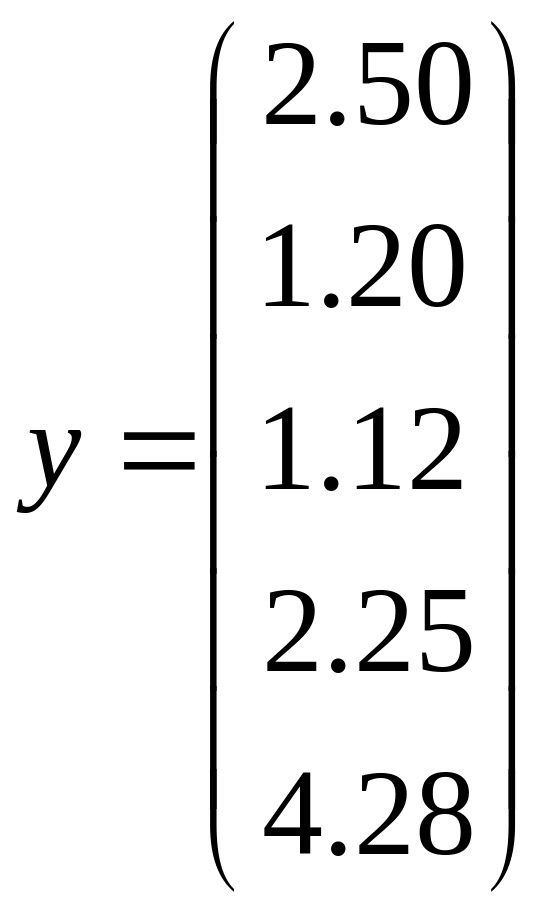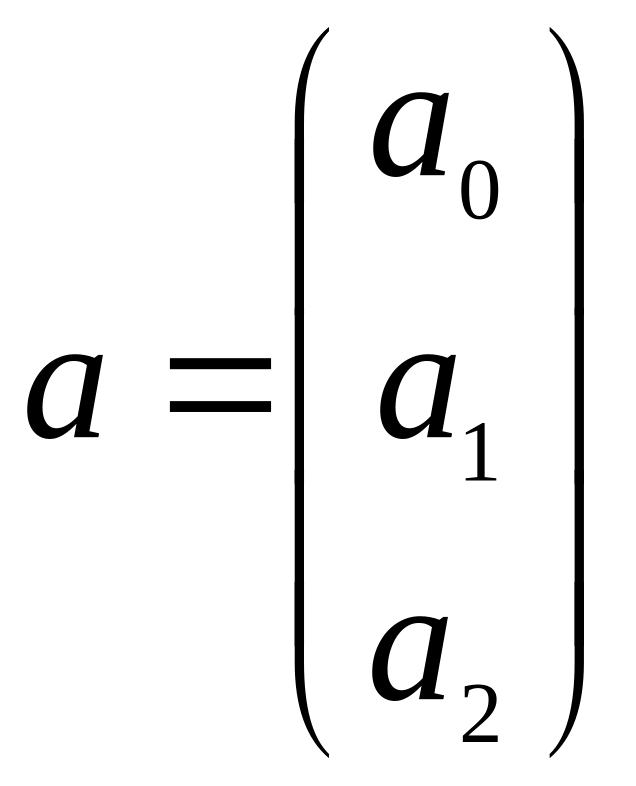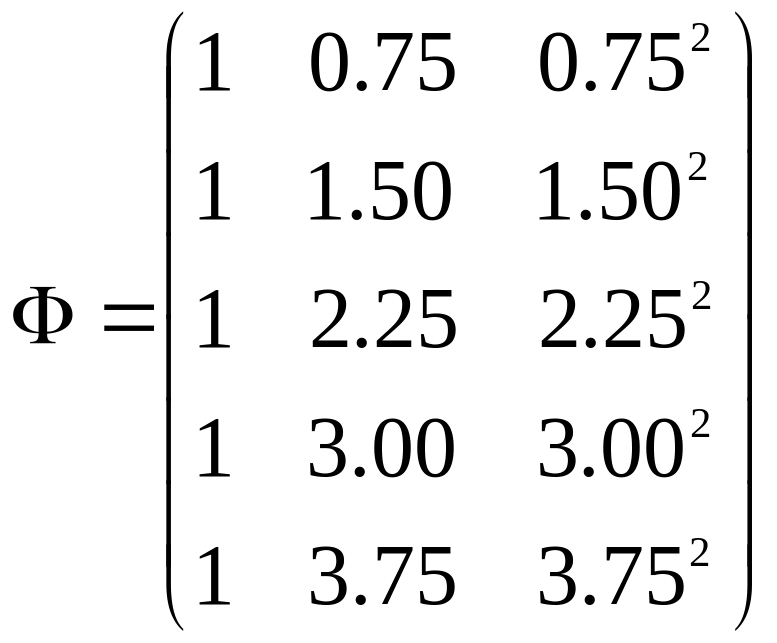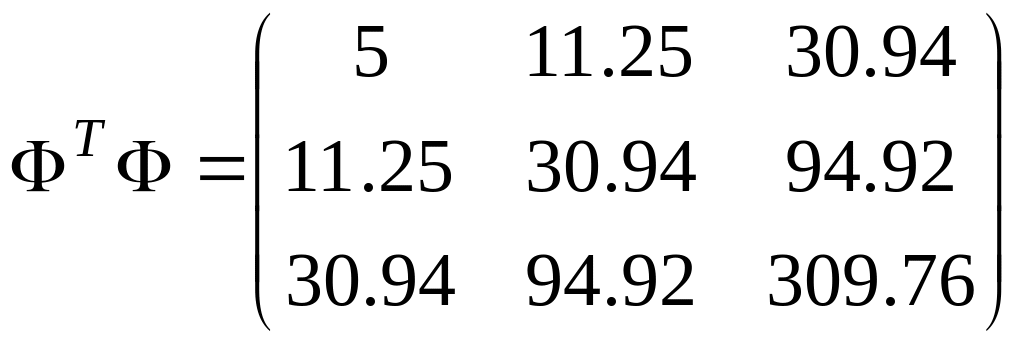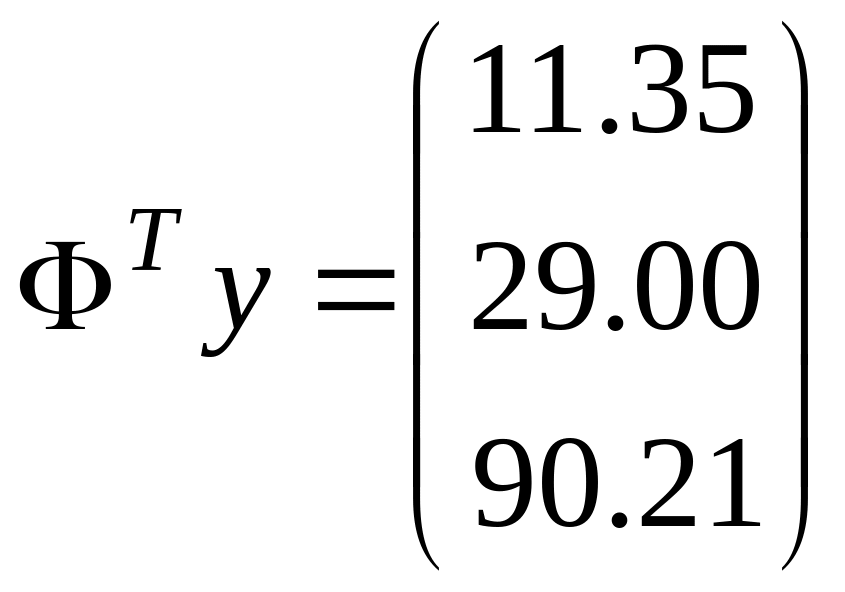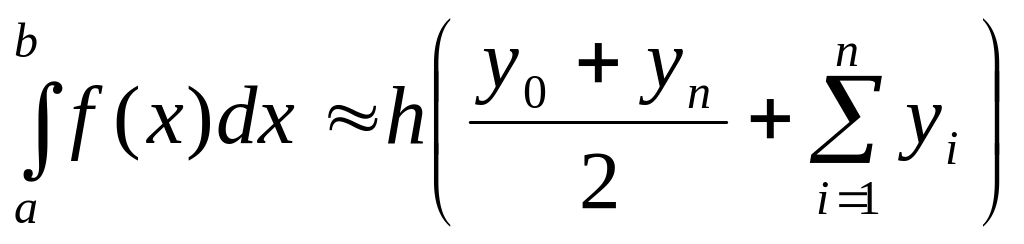Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности