Тема: Апроксимація функцій Теоретичні відомості Емпіричні формули

Нехай, вивчаючи невідому функціональну залежність між і , в результаті проведення експериментів було отримано ряд значень цих величин. Значення та записані у виді наступної таблиці:

		…
		…

Завдання полягає в тому, щоб знайти наближену залежність:

,

(8)

значення якої при ( ) мало відрізняються від спостережуваних даних . Наближена функціональна залежність (8), отримана за допомогою експериментальних даних, називається емпіричною формулою.

Простою емпіричною формулою є лінійна залежність виду:

.

(9)

Іншою простою емпіричною формулою є поліном другого ступеню:

.

(10)

Визначення параметрів емпіричної залежності

Вважатимемо, що тип емпіричної формули обрано і її можна представити у виді:

,

(11)

де – відома функція – невідомі постійні параметри. Тоді задача полягає в тому, щоб визначити такі значення цих параметрів, при яких емпірична формула дає найкраще наближення даної функції.

Тут не ставиться умова (як у випадку інтерполяції) збігу спостережуваних даних із значеннями емпіричної функції (11) у точках . Різницю між цими значеннями (відхилення) позначимо через . Тоді:

, .

(12)

Задача знаходження найкращих значень параметрів зводиться до мінімізації відхилень .

Існує декілька способів розв’язання цієї задачі. Один з них метод найменших квадратів.

Метод найменших квадратів

Запишемо суму квадратів відхилень (12) для всіх точок :

, .

(13)

Параметри емпіричної формули (11) знайдемо з умови мінімуму функції .

Оскільки тут параметри виступають в ролі незалежних змінних функції , то її мінімум знайдемо з необхідних умов екстремуму функції багатьох змінних, прирівнюючи нулю частинні похідні по цим змінним:

(14)

Отримані співвідношення визначають систему лінійних алгебраїчних рівнянь для визначення .

Розглянемо застосування методу найменших квадратів для широко використовуваного на практиці окремого випадку, коли функція є лінійною по невідомих параметрах :

,

де – відомі функції . Формула (13) для визначення суми квадратів відхилень прийме вид:

.

Для складання системи (14) знайдемо похідні по змінним ( ):

Прирівнюючи знайдені похідні нулю, отримаємо наступну систему рівнянь:

, .

(15)

Система (15) є системою лінійних алгебраїчних рівнянь, її можна записати в наочному векторно-матричному вигляді. Для цього введемо вектори точних даних і невідомих параметрів , а також матрицю наступним чином:

, , .

Тут вектори і мають розмірності і відповідно, а матриця має розмірність ( ) ( ). Для елементів матриці справедливий вираз:

.

Неважко переконатися, що вираз в квадратних дужках у (15), є -ю компонентою вектора , а кожне рівняння системи (15) є рівність нулю -ої компоненти вектора ( ), де – транспонована матриця. Таким чином, систему (15) можна записати у вигляді:

( )=0,

або:

.

(16)

Матриця цієї системи має розмірність ( ) ( ), вектор і є шуканим.

Приклад.

Використовуючи метод найменших квадратів вивести емпіричну формулу для функції , яка задана в табличному виді (таблиця 1):

Таблиця 1

	0,75	1,50	2,25	3,00	3,75
	2,50	1,20	1,12	2,25	4,28
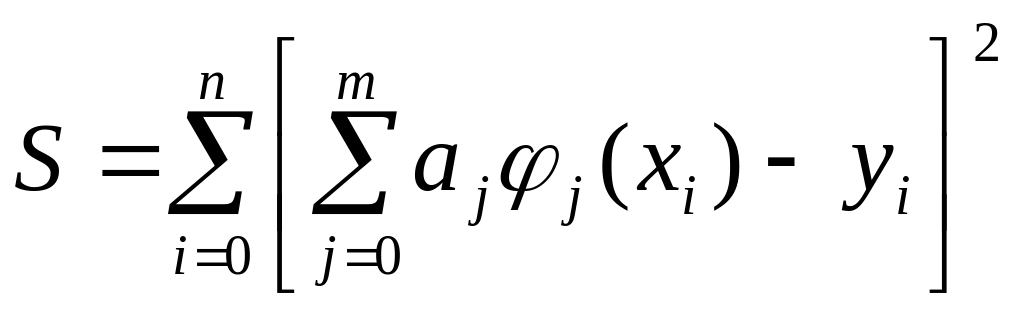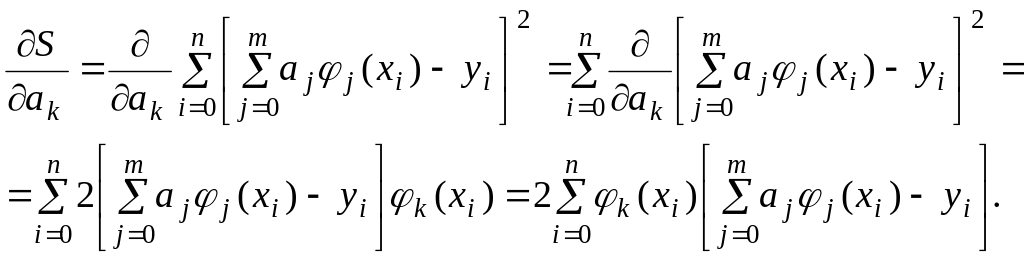
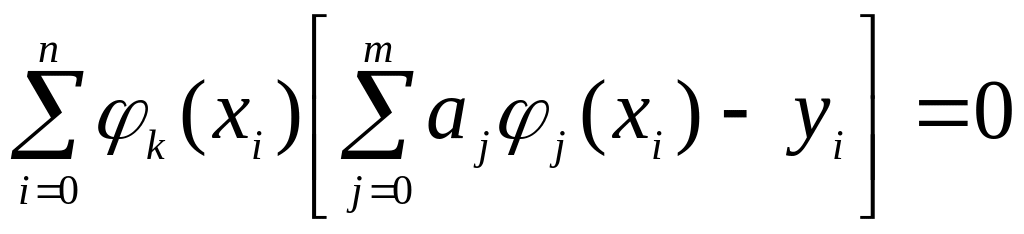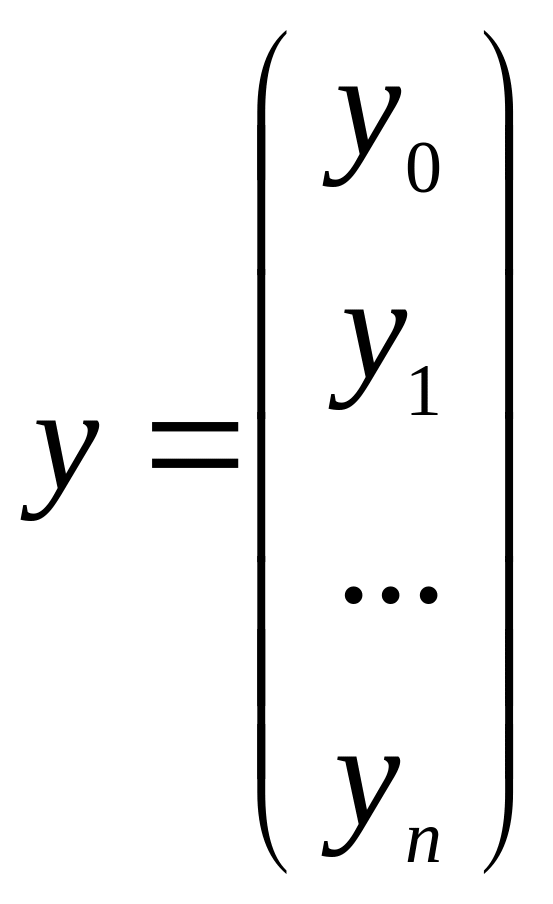
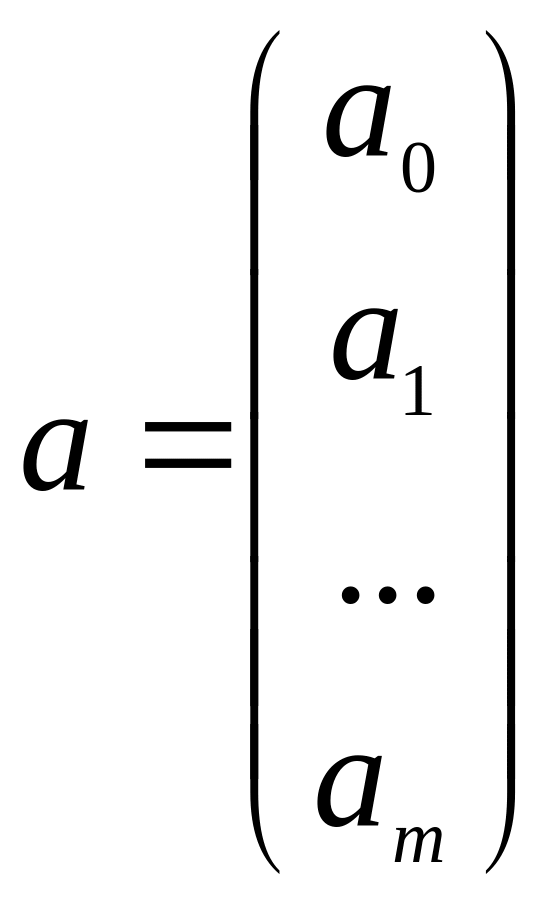
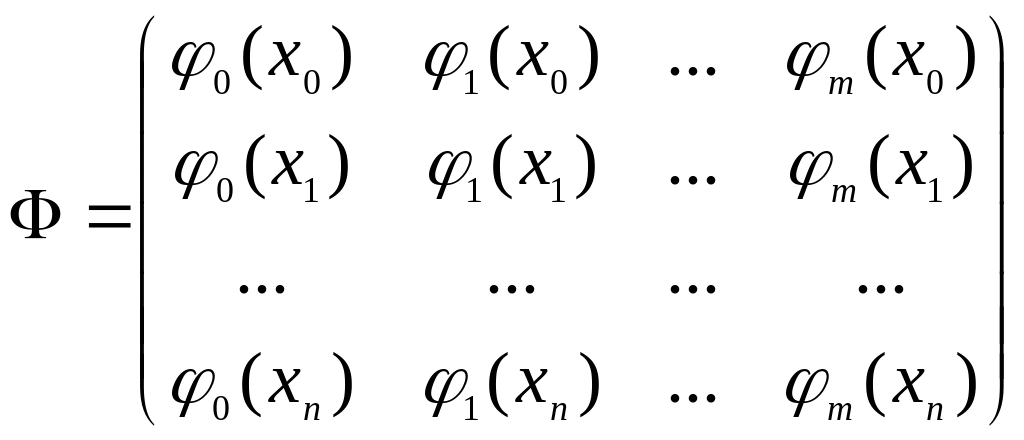