7.5. Обработка экспертных оценок

1. Составляется таблица рангов важности.

В столбцах оцениваемое события С_i.

В строках выставленные оценки каждым экспертом. Наибольшая оценка соответствует первому рангу важности и т.д.

Таблица 18. Ранги важности

		События Ci
		1	2	3
Оценки экспертов	Эксперт j=1	0,5	0,2	0,3
	Эксперт j=2	0,3	0,6	0,1
Ранг важности	Эксперт j=1	1	3	2
	Эксперт j=1	2	1	3
Суммарный ранг важности		3	4	5

Далее рассчитывается коэффициент конкордации W, алгоритм расчета демонстрируется примером. Пусть было десять событий m = 10 оцениваемых тремя экспертами: N, Q, R.

В 1, 2 и 3 строках – оценки, выставленные экспертом каждому событию.

4 строка – сумма значений в столбце, т.е. оценок всех экспертов. Все значения в четвертой строке суммируются и сумма делится на число событий, здесь на 10 = A.

Таблица 19. Расчёт коэффициента конкордации.

№	Эксперты	Оценка
1	N	1	4,5	2	4,5	3	7	6	9	7,5	10
2	Q	2,5	1	2,5	4,5	4,5	8	9	6,5	10	6,5
3	R	2	1	4,5	4,5	4,5	4,5	8	8	8	10
4		5,52	6,5	9	13,5	12	20	23	23,5	25,5	26,5	A=16,6
5		-11	-10	-7,5	-3	-4,5	3,5	6,5	7	9	10
6	2	121	10	56,25	9	20,25	12,25	42,25	49	81	100	2= Sv=591

5 строка – из значения в 4 строке вычитается величина А, т.е. среднее значение.

6 строка – значения из 5 строки в квадрате.

Значения 6 строки суммируется:

W=0,828

При анализе учитывается, что W приближается к нулю, если нет согласования в оценках и наоборот при W  1 эксперты демонстрируют полное согласие. Принято считать нормой W  0,5, когда наличие согласованности заметно, но нет оснований подозревать экспертов в сговоре. Норма W от 0,5 до 0,8.

7.6. Анализ экспертных оценок

Последующая обработка таблиц с экспертными оценками, приводится во многих учебных пособиях и теоретических источниках, как правило, в сопровождении пространных и сложных вычислений. Для практических задач сложные расчеты, обычно, избыточны, поскольку привносят риск ошибочной трактовки результатов. Выводы по таблице с экспертными оценками, могут быть корректными без длинных формул.

Упрощения можно начать с коэффициента конкордации, заменив его мерами погрешностей экспертных оценок.

Для определения погрешностей экспертных оценок рационально ввести побольше градаций по заданному событию – не менее 10. Задача эксперта – назвать самый привлекательный для покупателей товар и самую приемлемую цену. В дальнейшем, нужно, провести опрос покупателей по аналогичной тематике и найти разности.

Расчет коэффициента коркордации, равно как и формальные оценки для экспертов непременно вводятся в отчеты, поскольку являются убедительным для заказчиков подтверждением компетентности и добросовестности авторов. Между тем в изложенных расчетах накоплены методические погрешности, для многих задач чрезмерные.

Прежде всего, оценка компетентности экспертов, это тема вовсе не совпадающая с целями исследований. На достоверность оценок экспертов влияет ряд факторов, среди которых компетентность может не доминировать. Коэффициент конкордации не имеет связи с погрешностями оценок, им пользуются интуитивно, без объективного обоснования.

Для объективного контроля экспертных оценок необходимы данные о погрешностях, достаточные для эмпирической функции распределения. Функция распределения погрешностей экспертных оценок строится аналогично всем прочим, определяющим точность, и доступна расчетам с заданной достоверностью.

Оценки экспертов признаются равноценными во всех операциях их совместной обработки. В качестве исходной принимается “презумпция невиновности” эксперта в ошибке. Погрешности экспертных оценок определяются в основном при наличии количественных признаков, которые можно предъявить экспертам в форме вопросов, а затем точно определить. Такие вопросы можно рассматривать в качестве образцовых мер. При отсутствии таковых недоступна определению систематическая погрешность экспертных оценок. Случайная погрешность определима без образцовой меры. Необходимым условием является численная оценка с числом градаций не менее 10.

Каждая градация должна быть статистически значимой. Если к примеру 20 экспертов ставит десятибалльные оценки так, что баллы от 1 до 7 не используются вовсе, придется признать их оценки трехбалльными – 8, 9, 10. Затем ввести десятичные доли, как у гимнастов и повторить оценки. Требуется не менее четырех градаций, используемых экспертами, не реже, чем дважды для 20 оценок каждая.

При наличии значительного размаха в оценках, с доминированием экстремальных значений, надо уменьшить число градаций, обеспечивая статистическую значимость центра группирования погрешностей.

Оцениваемый экспертами признак должен быть доступен проверке, насколько это возможно. К примеру, оценки качества товаров по ряду признаков могут включать объемы продаж, уровни дефектности, цены и т.п. числа, прогнозируемые экспертами и определяемые в дальнейшем по фактическим данным. Все экспертные оценки вносятся на вероятностный график.

Самой типичной темой для экспертных оценок являются цена нового товара, планируемого для ввода на местный рынок, и объем продаж на неделю. Смысл оценок конкретизируется, к примеру, цена удовлетворяет не менее чем 10% потенциальных покупателей, а условия продаж приравниваются к некоторому товару, который есть в магазинах. Оценки экспертов представлены на рис.53.

После пробных продаж выяснилось, что цена нового товара, при которой не менее 10% потенциальных покупателей приобретают товар, составляет С_Ф = 1700 руб. Таким образом, систематическая погрешность экспертов составила +100 руб., а  - средняя квадратическая ошибка 200 руб.

Метрологическая аксиома – ошибка измерений, определяемая с образцовой мерой, определяет ошибки измерений всех выборок из исследуемой совокупности. В данном случае вводится допущение, что если среднее квадратическое отклонение _ф у избранного признака составляет 0,2 размаха, то все прочие признаки определяются с той же погрешностью. Предполагается также, что шкалы для всех признаков, включая качественные, выбраны корректно в равной степени, так что систематические погрешности идентичны у измерений, независимо от признака.

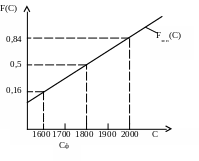
Рис. 53. Вероятностный график экспертных оценок

В отличие от измерительных средств, эксперты доступны замене в произвольной последовательности. При известных погрешностях измерений доступны объективной оценке вклады экспертов в ошибку. Здесь отклонения от аппроксимирующей прямой F(x) рассматриваются как промахи. Если некий эксперт допускает промахи неоднократно, то его полезно исключить, несмотря на его, возможно, высокую компетентность. Столь же нежелательная альтернативная ситуация когда несколько экспертов дают одинаковые оценки многократно. Повторяющиеся оценки наиболее правдоподобные, являются основанием для комплектования будущей группы экспертов.