5.2. Предварительный статистический анализ (пса)

ПСА производится в процессе накопления данных в информационной системе, обеспечивая их классификацию и структурирование, а также минимизацию ошибок в процессе сбора и обработки информации.

В ПСА уточняются правила заполнения первичных форм учета, состав и содержание фиксируемых данных.

Все данные, накапливаемые информационной системой, делятся на три вида:

1. Эмпирические данные. «Эмпирику» получают непосредственно в производстве или в ходе экспериментов. Данные количественные, необходимые для моделей расчетных, считывают с приборов, записывают при испытаниях, считывают по анкетам и т.д. Эмпирические данные записывают:

• в табличной форме;

• в графической форме.

Таблица и график могут быть взаимозаменяемыми. Таблица проще в исполнении и точнее представляет данные. График «доходчивее» позволяет обнаруживать тенденции в поступающих данных, интерполировать или экстраполировать, и т.д. Сегодня прикладные программы обеспечивают вывод данных в обеих формах, по выбору оператора.

2. Теоретические данные. Теоретический аппарат является продуктом деятельности математиков и проектировщиков. Количественные данные в расчетных моделях являются гипотетическими, т.е. плодами интеллектуальной деятельности. Эти данные могут быть представлены в аналитической форме, в виде формул или в ином символьном представлении, а также и табличной и в графической формах.

Теоретические и эмпирические графики часто объединяют для сравнения, иллюстрируя степень их адекватности. Аналогично поступают с таблицами.

3. Опубликованные данные, заимствованные из официальных источников. Нормативно-техническая документация: от ГОСТов до стандартов предприятия, справочники и реклама, периодика и профессиональные книги, итоги семинаров и деловых встреч. НТД регламентирует номинальные и предельные значения на все количественные признаки. Номиналы и допуски являются, естественно, детерминированными значениями.

Таким образом, к известным и неизвестным величинам в расчетах, привычным со школы, добавляются величины детерминированные и статистические, и, кроме того, величины собственные и заимствованные.

Заимствованные или цитируемые величины могут быть приведены в разнообразных интерпретациях и без сведений об их достоверности. При необходимости их совместного анализа может потребоваться их обработка по методике, отличной от авторской.

В практических задачах совместно используются и эмпирические и теоретические данные. Прикладные программы сопоставляют все данные в табличной форме, поскольку это гораздо удобнее для цифровой обработки.

Однако никакие программы не могут предугадывать стратегию анализа и, тем более, синтеза, так что необходим диалог с оператором – интерактивный режим.

Человек воспринимает графики несравненно быстрее и достовернее, чем таблицы и, тем более, формулы. Поэтому диалог с ЭВМ рациональнее вести в графической форме. Выбор графической интерпретации становится единственно возможным для необозримо объемных массивов цифр и формул с труднодоступным смыслом.

Применение статистических расчетов в практических задачах привносит риск ошибок из-за неопытности или нерадивости работника.

Нечто подобное было при компьютеризации менеджмента, однако своевременно появились книги, типа «Компьютер для чайников». К сожалению, нет на сегодня «Матстатистики для чайников».

Статистическая литература изложена весьма корректным математическим языком. Если практические задачи не укладываются в Прокрустово ложе математической модели, то никаких рекомендаций по их решению не отыскать. К сожалению, идеальная для математики практика является, скорее, исключением, чем правилом.

В этом пособии используется исключительно графическая интерпретация всех маркетинговых задач. Расчетные формулы не используются, приводятся пояснения для решений, доступных и полезных в практической деятельности.

Инженер и маркетолог, применяющие статистические расчеты, обретают значительное конкурентное преимущество, ради которого есть смысл преодолеть неприятие, воспитанное вузом. Освоение стохастического моделирования, это не просто вооружение новым инструментом, это рост уровня мышления. Видя, к примеру, рекламу с исхудавшей дамой, поедающей некое средство, уже не придется бежать за покупкой. Вспомнятся риски симптомов, не упомянутых в рекламе, и меры рассеяния веса худеющих.

В экономических учебниках обычно приводятся графики хозяйственной деятельности за много лет. Замысловатая зависимость от времени вала или цен объясняется по детерминированной модели. Обычно ищется колебательный процесс с периодом и амплитудой колебаний. Спад рассматривается, как непременный предвестник подъема – вроде качелей.

Стохастическая модель отрицает связь соседних значений, так что по предыдущему значению нельзя прогнозировать последующее аксиоматически. В любой точке спада может быть рывок и вверх и вниз. Источников гармонических колебаний может не быть вовсе, а причины случайных флюктуаций всегда налицо.

Стохастические модели описывают случайные процессы, состоящие в чередовании множества значений исследуемых признаков. Моментные оценки случайных процессов представляют случайные величины. Множество измерений исследуемого признака или предполагаемых его значений составляет статистический ансамбль.

Математики предлагают устремить к бесконечности исследуемое множество, и называют его генеральной совокупностью.

В практических задачах оперируют множествами с конечными объемами. Изделия, в частности, или товары, характеризуют объемами партий N. Партия является целью исследований, причем часто недоступной из-за непомерных затрат или физических ограничений. Партию представляют в качестве статистического ансамбля при ее чрезмерном для исследований объеме, например, более 10⁵.

Для исследования партии применяют эмпирические распределения (ЭР), для чего комплектуют по обоснованным правилам выборки с объемом n. Правила составления выборки должны гарантировать случайность, т.е. равные шансы отбора у всех элементов. Иллюстрацией этих правил является смешивание шаров в барабане и участие ребенка в изъятии шара. Отбор из партии элементов выборки должен обеспечивать равенство статистических показателей партионных и выборочных т.е. представительность выборки. ЭР может быть представлено графически или таблично колонками цифр.

Стохастическая модель оперирует теоретическим распределением (ТР) случайной величины. ТР – это средство исследования статистического ансамбля, представляемое в аналитической форме. Кроме того, оно представляется в графической и табличной формах. Аналитическая форма создается математиком посредством весьма сложных выкладок, приближающих модель к избранным объектам. По формулам создаются программы, формирующие таблицы и графики в компьютере для сравнения с эмпирическими данными. Значения случайной величины принято назы

Рис. 21. Гистограмма распределения.

вать реализациями. Эмпирические распределения составляются показаниями приборов, записями в анкетах и т.п.

Известно несколько вариантов графического представления стохастических моделей. Самой широкоупотребительной, а во многих источниках единственной, является гистограмма распределения.

Известные методики построения гистограмм отличаются разнообразием, так что не всегда возможно совмещение данных из разных источников.

Общим для всех методик является размещение под горизонтальной осью с линейным масштабом Х всех значений исследуемого признака Х_i. Значения откладываются в виде точек в соответствии с избранным масштабом. Здесь и далее горизонтальная ось называется параметрической, а выборка - упорядоченной.

Параметрическую ось делят на несколько равных интервалов и подсчитывают число точек в каждом интервале – «частость». Частости n_i откладывают по вертикальной оси, предварительно поделив на общее число значений n. Сумма относительных частостей во всех интервалах равна единице.

В университетах США студентам показывают физические модели распределений. Это наклонные доски, с которых скатываются шарики. Низ доски разделен барьерами на «загоны» для шариков. На доске имитируются воздействия на шарики, формирующие распределение их между барьерами. Множество скатывающихся шариков создает иллюстрацию теоретического распределения внизу доски. Старт шариков – в центре верха доски.

Причины рассеивания имитируются шпильками, установленными на пути шариков. В результате соударений шарики катятся к разным барьерам, «материализуя» гистограмму на нижней кромке.

Для любого теоретического распределения можно рассчитать форму гистограммы, задавшись числом интервалов и предположив бесконечный объем партии. О теоретических распределениях есть обширная библиотека, причем каждое распределение, а их более 300, построено на конкретных условиях. Выбор теоретического распределения для практической задачи можно уподобить составлению фоторобота в криминалистике. В науке можно найти аналогию с изучением спектральных линий, определяющих наличие примесей в веществе.

На рис. 21 представлена гистограмма с эмпирическими значениями в виде точек и прямоугольниками, высота которых пропорциональна числу точек в интервале. Подобные гистограммы часто приводятся в литературе. Их форма зависит не только от представленных данных, но и от методики построения.

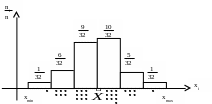
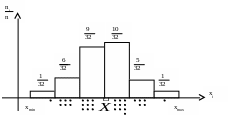
Известные методики различаются по приемам выбора числа интервалов, размещения крайний интервалов относительно экстремальных значений, учета точек на границах интервалов и т.п. Различия существенны, при необходимости сравнения гистограмм из разных источников приходится перестраивать их по одной методике.

Для обработки эмпирических данных рекомендуется следующая методика построения гистограммы:

1. Число измерений (реализаций) фиксировано n = 32.

2. Все значения размещаются под горизонтальной (параметрической) осью в виде точек. Отмечаются максимальные X_max и минимальные X_min значения, а также срединное – медиана 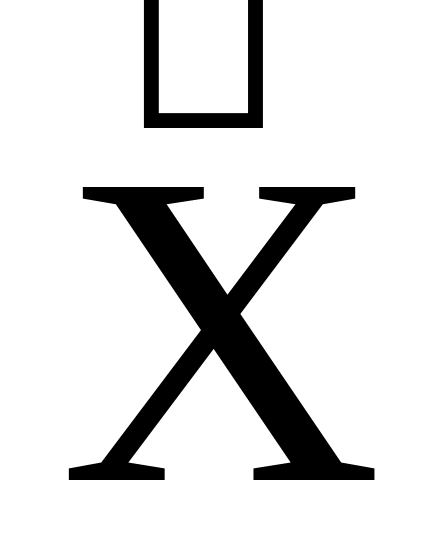, для чего отсчитывается 16 точек справа и слева.

3. От медианы откладывается вправо и влево по три равных интервала так, чтобы все точки оказались внутри интервалов при наименьшей их ширине.

4. Подсчитывается число точек в интервалах, причем, точки на границах интервалов разносят на обе стороны пополам. Строятся прямоугольники с высотой, пропорциональной числу точек в интервале.

В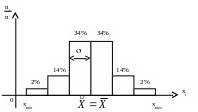 гистограмме «заложена» методическая погрешность из-за смешивания точек в интервале, поэтому большие выборки избыточны. Фиксированное число точек устраняет вариацию гистограмм из-за разных объемов. Построение интервалов от центра, а не от краев, как это принято, обосновано тем, что вариация экстремальных значений значительно больше, чем у медианы. Использование 6 интервалов вытекает из общеизвестного правила «3». Если наблюдаемая выборка представительна и соответствует этому правилу, то медиана равна среднему арифметическому значению , а ширина интервала равна . Эмпирические гистограммы доступны сравнению с теоретической по правилу «3», у которой число значений в интервалах составляет:

Рис. 22. Теоретическая гистограмма распределения.

Среднее арифметическое значение или просто среднее является самым широко известным статистическим показателем. Оно просто рассчитывается, тем более, с калькулятором – складываются измерения, а сумма делится на число измерений.

По гистограмме прочесть среднее еще проще, причем, одновременно оценивается форма. Если форма отличается от названного выше правила, то расчет теряет смысл. Равно как и , хоть его и рекомендуют считать по соответствующей формуле.

Гистограмму рационально применять при приближенных, ориентировочных оценках распределений эмпирических данных. Прежде всего, устанавливается сам факт наличия статистической информации – наличие различающихся значений х_i количественного признака Х . Если все значения совпадают, надо считать признак детерминированным. Различия значений х_i позволяет составить упорядоченную выборку, в которой значения выстраиваются «по росту» от х_min до х_max. Говорят о ранжировании Х – именно для этого удобна параметрическая ось.

Комплект измерений Х определяет вариацию признака Х с размахом

R = x_max – x_min.