2.2. Молекулярная физика и термодинамика

Пример 2.1. (С2). В водонепроницаемый мешок, лежащий на дне моря на глубине 73,1 м, закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и когда объем воздуха в мешке достигает 28,0 м, мешок всплывает вместе с прикрепленным к нему грузом. Масса оболочки мешка 2710 кг. Определите массу груза. Температура воды равна 7°С, атмосферное давление на уровне моря равно 10 Па. Объемом груза и стенок мешка пренебречь.

В основе решения этой задачи условие, при котором мешок с грузом начнет всплывать: ρVg = Mg + m_rg + m_вg, где М и m_r — масса оболочки мешка и масса груза, V и m_в — объем и масса воздуха в мешке, ρ — плотность воды. Следовательно, m_r = ρV - М - m_в.

Так как мешок заполнен воздухом, то к его состоянию применимо уравнение Менделеева-Клапейрона: pV =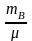 RT, где давление воздуха на заданной глубине h можно выразить формулой р = р₀+ ρgh, где р₀ — атмосферное давление.

П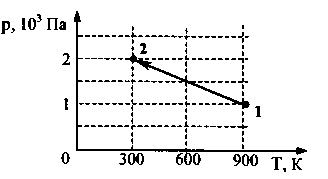 ример 2.2. (С2). Bo время опыта объем сосуда с воздухом увеличился в 1,5 раза, и воздух перешел из состояния 1 в состояние 2 (см. рисунок). Кран у сосуда был закрыт неплотно, и сквозь него мог просачиваться воздух. Рассчитайте отношение 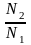числа молекул газа в сосуде в конце и в начале опыта. Воздух считать идеальным газом.

Основу решения задач этого типа составило уравнение состояния идеального газа в виде р = nkT, где n = - концентрации молекул газа. Отсюда легко получить ответ в общем виде и числовой ответ.

.

Пример 2.3. С(2). Сосуд разделен пористой перегородкой на две равные части. В начальный момент в одной части сосуда находится 2 моль гелия, а в другой - такое же количество аргона. Атомы гелия могут диффундировать (проникать) через перегородку, а для атомов аргона перегородка непроницаема. Температура гелия равна температуре аргона Т = 300 К. Определите отношение давлений газов на перегородку с разных сторон после установления термодинамического равновесия.

В решении такого рода задач необходимо было рассмотреть состояние системы после установления термодинамического равновесия: в каждой части сосуда окажется по 1 молю гелия. В результате в сосуде с аргоном окажется 3 моля смеси, а с другой стороны перегородки останется 1 моль гелия. Запись уравнения Клапейрона-Менделеева для каждой части сосуда позволит определить давление гелия и смеси: P_HeV=RT и P_He+ArV = 3RT, где 2V – объем сосуда. Решение этих уравнений и приведет к ответу на заданный в задаче вопрос.

Пример 2.4. С(2). Цилиндрический сосуд, расположенный горизонтально, разделен тонким поршнем на две равные части. В одной части сосуда находится 1 кг гелия, а в другой - 1 кг аргона. В начальном состоянии поршень удерживается внешними силами. Поршень отпустили, и через некоторое время система пришла в состояние равновесия с окружающей средой, температура которой Т = 300 К. Какую часть цилиндра занимает гелий после установления равновесия? Трением поршня о стенки сосуда пренебречь.

Задача предполагает рассмотрение системы после установления механического и теплового равновесия: давление гелия и аргона на поршень должно быть одинаковым, и температура газов также одинакова р_Нe= р_Ar, = р, Т_Не = Т_Ar = Т.

Применение уравнения Клапейрона-Менделеева pV_He = ν_HeRT, pV_Ar = ν_ArRT, где ν_Ar=m_Ar/M_Ar, ν_Ar, - число молей аргона, a ν_He=m_He/M_He - число молей гелия, позволяет получить отношение объемов (учитывая равенство масс газов m_Нe = m_Aг = m): 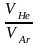= 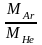. Но объем сосуда после установления равновесия не изменился V_He + V_Ar=V, поэтому легко найти искомое отношение = .

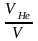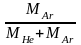Решение следующего цикла задач было основано на понимании школьниками двух тем, вызывающих затруднения уже на уровне обязательного минимума содержания образования – «Первый закон термодинамики» и «Закон сохранения импульса» для случая неупругого соударения, рассмотренных нами выше. Результатом отсутствия понимания смысла этих законов на базовом уровне явилось причиной того, что ни один из участников экзамена не справился с такого рода задачами (пример 2.5).

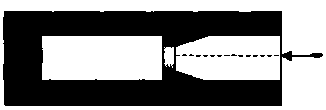Пример 2.5. С(6.) В вакууме закреплен горизонтальный цилиндр. В цилиндре находится 1 л гелия, запертого поршнем, при давлении 100 кПа и температуре 300 К. Поршень массой 90 г удерживается упорами и может скользить влево вдоль стенок цилиндра без трения. В поршень попадает пуля массы 10 г, летящая горизонтально, и застревает в нем. Температура гелия в момент остановки поршня в крайнем левом положении возрастает на 90 К. Какова скорость пули? Считать, что за время движения поршня газ не успевает обменяться теплотой с цилиндром и поршнем.

Решение задачи основано на законе сохранения импульса при неупругом соударении: mv₀ = (m + M)v_n. Отсюда: v_n=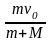 , где m и М - соответственно масса пули и масса поршня, v₀ - скорость пули, v_n - скорость поршня после попадания пули.

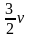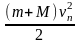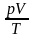Формула для расчета внутренней энергии одноатомного идеального газа U = RT, и учет того, что механическая энергия поршня с пулей превращается во внутреннюю энергию гелия, дает возможность рассчитать ΔU: ΔU = RΔT = . Из уравнения Менделеева – Клапейрона следует, что νR = . Решение системы уравнении дает: v₀ = .
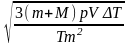