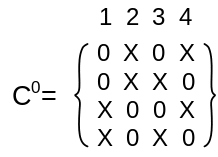3.2. Выполнение обратной импликации для нулевого и единичного значений на выходе кс

Кубические покрытия (КП) для одновыходовых схем условно можно разделить на две части:

C⁰ – кубы, имеющие символ 0 на выходной координате;

C¹ – кубы, имеющие символ 1 на выходной координате.

Одним из основных свойств КП является условие: C⁰ C¹ = 

Если указанное правило не соблюдается, то КП построено неверно.

Правильно построенное КП должно отвечать условиям полноты и минимальности.

КП называется полным, если его кубы "покрывают" все 2ⁿ входных наборов ЛФ и не существует ни одного полностью определенного входного набора, который не принадлежал бы какому-либо кубу КП.

КП называется минимальным, если ни для одного из его кубов не выполняется условие C_i¹ C_j¹ или C_i⁰ C_j⁰ для любых i или j.

Используя описание ЛЭ в форме КП, можно реализовывать две основных операции анализа логических схем:

обратную импликацию – получение входных значений по известному выходному.

прямую импликацию – получение выходного значения по известным входным;

Обратная импликация для цифровой схемы состоит в вычислении множества входных значений сигналов, подавая которые на схему можно получить требуемые выходные значения.

3.2.1. Алгоритм выполнения обратной импликации

3.2.1.1. Выбирается требуемый вариант доопределения (для нулевого или единичного значения на выходе схемы) и на его основе формируется доопределяемый вектор T.

3.2.1.2. В доопределяемом векторе T анализируются линии схемы, начиная от максимального номера, и выбирается первая, не равная X. Она становится линией связи L_С. Выполняется пересечение доопределяемого вектора с КП ЛЭ, для которого L_С является выходом (выбирается тот тип покрытия C⁰ или C¹, который соответствует значению линии L_С 0 или 1). Результаты непустых пересечений вместе с номером последней доопределенной L_С записываются в промежуточный массив результатов доопределения.

3.2.1.3. Из промежуточного массива доопределения выбирается очередной вектор и для него повторяется п.2, начиная от последней L_С.

3.2.1.4. Пункты 2 и 3 повторяются до тех пор, пока все внутренние линии схемы для вектора, выбранного в пункте 3.2.1.1, не будут доопределены (очередная выбранная линия принадлежит внешним входам), или промежуточный массив доопределения не станет пуст. Если доопределение для выбранного в п.1 вектора завершено успешно, полученный результат записывается в массив результатов доопределения. Если результата доопределения не существует, то делается вывод о невозможности осуществления выбранного в п.1 варианта доопределения.

3.2.2. Пример выполнения обратной импликации для кс

Выполним обратную импликацию для нулевого значения на выходе КС вентильного эквивалента 22И-ИЛИ (рисунок 3.2).

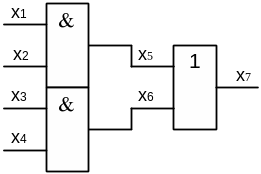
Рисунок 3.2 – Схема вентильного эквивалента 22И-ИЛИ

x1 x2 x3 x4	x5 x6	x7	Примечания
X X X X	X X 0 0	0 0	Исходный вектор доопределения T, LС = 7 C01 (линия 7, ЛЭ ИЛИ)
X X X X     0 X     X 0	0 0 0 0	0	T1 = T  C01, LС = 6 C01 (линия 6, ЛЭ И) C02 (линия 6, ЛЭ И)
X X 0 X X X X 0 0 X     X 0	0 0 0 0 0 0	0 0	T2 = T1C01, LС = 5  T3 = T1C02, LС = 5 C01 (линия 5, ЛЭ И ) C02 (линия 5, ЛЭ И )
0 X 0 X X 0 0 X 0 X X 0 X 0 X 0	0 0 0 0 0 0 0 0	0   0   0   0	T4 = T2C01 T5 = T2C02 T6 = T3C01 T7 = T3C02

L_С – координата связи;

T_i – очередной доопределяемый промежуточный вектор;

Cⁱ_j – j-й куб покрытия i-го типа, i = 0, 1 ( покрытия C⁰ или C¹).

Доопределяемая на текущем шаге координата выделена жирным стилем.

В каждой строке таблицы выделено пересечение с кубами соответствующего доопределяемого элемента.