- •Правила оформлення звіту по лабораторній роботі
- •Позначення лабораторних і практичних робіт
- •Журнал лабораторних робіт
- •Критерії оцінювання навчальних досягнень студентів при виконанні лабораторних та практичних робіт
- •Критерiї оцiнювання навчальних досягнень студентiв при виконаннi лабораторних та практичних робiт
- •Визначення прискорення тіла у рівноприскореному русі
- •Порядок виконання роботи
- •Контрольні запитання
- •Дослідження руху тіла по колу під дією сил пружності і тяжіння
- •Теоретичні положення:
- •Порядок виконання роботи
- •Контрольні запитання
- •Вивчення одного з ізопроцесів
- •Теоретичні положення:
- •Порядок виконання роботи
- •Контрольні запитання
- •Вимірювання відносної вологості повітря
- •Теоретичні положення:
- •Порядок виконання роботи
- •Контрольні запитання
- •Теоретичні положення
- •Порядок виконання роботи
- •Контрольні запитання
- •Визначення е.Р.С. І внутрішнього опору джерела електричної енергії
- •Теоретичні положення
- •Порядок виконання роботи
- •Контрольні запитання
- •Спостереження дії магнітного поля на провідник зі струмом.
- •Теоретичні положення
- •Порядок виконання роботи
- •Контрольні запитання
- •Визначення прискорення вільного падіння за допомогою математичного маятника.
- •Теоретичні положення
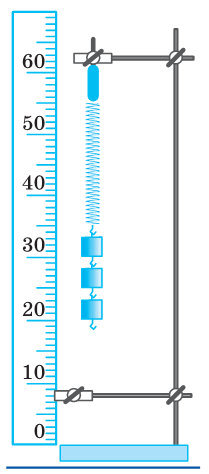
- •Період коливань пружинного маятника
- •Порядок виконання роботи
- •Контрольні запитання
- •Визначення абсолютного показника заломлення скла
- •Теоретичні положення
- •Порядок виконання роботи
- •Контрольні запитання
- •Визначення довжини світової хвилі за допомогою дифракційної решітки
- •Теоретичні положення
- •Порядок виконання роботи
- •Контрольні запитання
- •Дослідження суцільного і лінійчатих спектрів
- •Теоретичні положення
- •Порядок виконання роботи
- •Контрольні запитання
Визначення прискорення вільного падіння за допомогою математичного маятника.
Мета роботи: вивчення законів коливання математичного та пружинного маятників.
Завдання:
1. Перевірити залежність періоду вільних коливань математичного маятника від довжини нитки.
2. Експериментально перевірити теоретичну формулу періоду коливання пружинного маятника
3. Визначити прискорення вільного падіння
Обладнання та інструменти: математичний маятник, пружина, комплект тягарців, секундомір, лінійка.
Вказівки на теоретичний матеріал:
Коливання математичного маятника.
Коливання пружинного маятника.
Теоретичні положення
Рисунок 1 |
Математичний маятник – це тіло масою m, яке можна вважати матеріальною точкою, підвішене на невагомій нерозтягуваній нитці. Знайдемо період коливань такого маятника. Якщо нитку відхилити від вертикального положення, виникає зворотний момент сили тяжіння mg, плече якої дорівнює L·sinα (рис.3.2). Під дією цього моменту тіло m обертається навколо точки підвісу О. Записуємо основне рівняння динаміки обертального руху
Тут:
|
враховує, що момент сили mg зменшує кут α.
Одержуємо диференціальне рівняння незатухаючих коливань математичного маятника
![]() (2)
(2)
|
При малих кутах α (менших 5о) можна вважити, що sinα = α. Одержуємо
Порівнюючи це рівняння із загальним рівнянням незатухаючих гармонічних коливань
|
маємо
![]() - циклічна
частота коливань,
- циклічна
частота коливань,
Т – період коливань математичного маятника.
Прийнявши L = L0 + ΔL, одержуємо
![]() .
(5)
.
(5)
Піднесемо це рівняння до квадрату
![]() . (6)
. (6)
Видно, що залежність квадрату періоду Т2 від зміни довжини нитки ΔL за теорією повинна бути лінійною, а її нахил визначається прискоренням вільного падіння g.
Розв’язком рівняння (3.4) є рівняння незатухаючих гармонічних коливань
![]() .
(7)
.
(7)
Рисунок 3 |
Пружинний маятник – це тіло підвішене на пружині. При виведенні його із положення рівноваги xo на відстань x виникає сила пружності F, яка за законом Гука дорівнює F = -kx (8) де k – жорсткість пружини. Ця сила надає тілу прискорення
Рівняння (1.1) запишемо так
Позначивши
|
Рівняння (11) називається диференціальним рівнянням незатухаючих вільних гармонічних коливань. Розв’язком цього рівняння є гармонічна функція
![]() , або
, або
![]() ,
(12)
,
(12)
яка задає координату х тягарця в будь-який момент часу t.
Розглянемо характеристики гармонічних коливань.
Амплітуда Ао – найбільше відхилення точки від положення рівноваги,
Циклічна частота коливань це кількість коливань за 2π секунд
![]() –
(13)
–
(13)
Період коливань – це час одного повного коливання, або час, за який фаза коливання змінюється на 2π
![]() –
(14)
–
(14)
.
Частота коливань – це кількість коливань за 1 секунду
![]() – (15)
– (15)