3. Контрольный пример

Задание. Построить логическую схему последовательного компаратора для сравнения 2 двоичных чисел А, В произвольной длины, поступающих на вход, начиная с младших разрядов. По окончании подачи чисел А, В на вход компаратора на его выходе должны появиться сигналы: y₀, если А=В, y₁ если A<B, у₂ если A>B, у₃.

Решение.

1. Введем в рассмотрение входные буквы: x₀₀, х₁₁, x₀₁, х₁₀, где нижний первый индекс соответствует значению текущего разряда числа А, а второй — числа В. С точки зрения сравнения чисел А, В действие букв x₀₀, х₁₁ равносильно, что позволяет их рассматривать как одну букву, обозначаемую в дальнейшем x₀.

2. Формализуем условия работы искомого автомата на языке регулярных выражений, эти условия приобретают вид:

(3.1)

(3.2)

(3.3)

Здесь итерационные скобки { }+={ }*e, где е – пустая буква,

введена для сокращения длины записи регулярных выражений.

Полученный граф — рис. 3.1 содержит три финитные вершины 1, 3, 4, соответствующие выходным реакциям у₀, y₁, y₂.

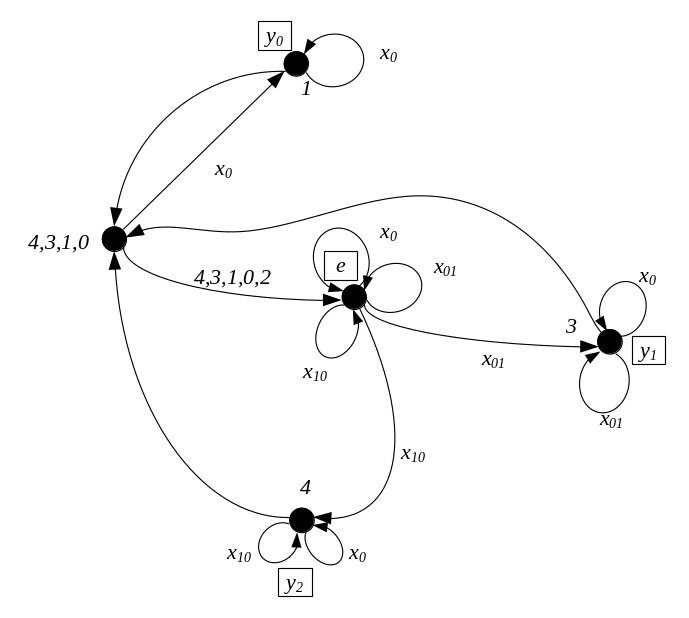
Рис. 3.1. Обобщенный граф регулярных выражений (3.1) – (3.3)

«Нейтральная» вершина 2 помечена пустой буквой е. Каждая финитная вершина с помощью пустой стрелки замыкается на начальную вершину, что соответствует воспроизведению итерационных скобок { }+. Номера вершин, «переносимых» по пустым стрелкам выписаны через запятую слева относительно вершин 0 и 2.

3. Переходим к построению обобщенного графа регулярных выражений (3.1) – (3.3).

4. Применяя методику детерминизации графа регулярных выражений (раздел 1.1), приходим к табл. 3 I.

Таблица 3.1

Вых.	–
Сост.	0	1 2	2 3	2

x₀ 1 2 1 2 2 3 2 4

x₀₁ 2 3 2 3 2 3 2 3

x₁₀ 2 4 2 4 2 4 2 4

Отсутствие противоречий при определении дизъюнкций выходных сигналов в табл. 3.1 свидетельствует о том, что система регулярных выражений (3.1) – (3.3) является корректной.

В дальнейшем при определении реакций автомата y₀, y₁, y₂ пустой символ, е можно не учитывать.

5. Переходим к эквивалентному автомату Мили, открывающему возможность получения абстрактной схемы наименьшей сложности (по числу состояний). Первоначальная модель содержит 4 состояния: . Так как разбиение не поддается расщеплению (совпадает с разбиением ), убеждаемся, что изображенный на рис. 1.2 – минимальный автомат.

6. Для проверки результатов абстрактного синтеза, а в случае неудачи (несоответствие поведения автомата техническому заданию, отсутствие видимых способов получения корректного описания), индуктивно воспроизводим дерево управления искомого автомата – рис. 1.1. Приняты следующие соглашения. Каждый «веер» ребер слева направо определяется входными буквами соответственно. Все ребра дерева помечены цифрами 0, 1, 2, соответствующими выходным реакциям . Дерево построено в предположении, что r=1, d=1, и потому имеет высоту h==3.

На дереве ясно просматриваются 3 различимые вершины базиса. Остальные зачеркнутые на рис. 1.1 вершины не отличимы от вершин базиса. Свертки дерева управле­ния приводят к точной копии искомого автомата (рис. 1.2).

Заметим, что все дуги, входящие в каждое из его состояний, помечены одинаковыми реакциями. Следовательно, граф на рис. 1.2 можно также рассматривать и как автомат Мура (рис. 3.2), что может дать некоторые преимущества на этапе структурного синтеза.

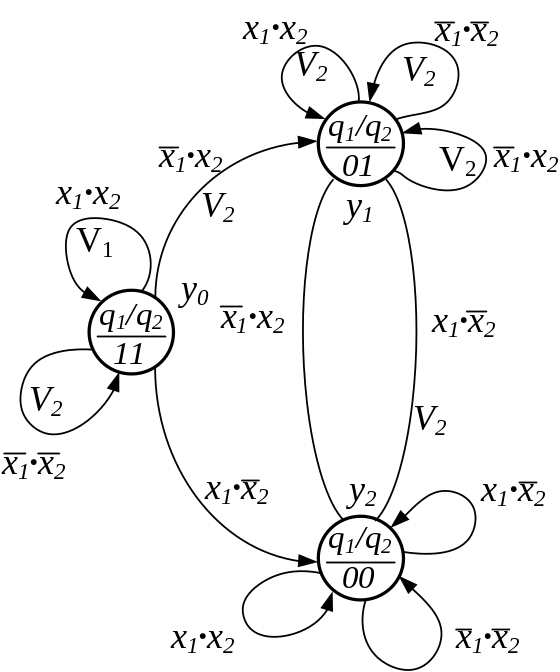
Рис. 3.2. Кодированный граф переходов

7. В качестве элементарного автомата выбираем D-триггер. Минимально возможное число D-триггеров – ]log23[=2. Рассмотрим вариант неудачного кодирования состояний абстрактного автомата: , который приводит, во-первых, к усложнению КЛС, во-вторых, к возникновению состязаний ЭА. Так, при переключении из состояния в состояние под воздействием для промежуточного состояния на выходе автомата будет получен сигнал вместо требуемого сигнала . Значительно более удачным является вариант кодирования, представленный на рис. 3.2.

Каждому состоянию автомата приписано единичное значение одного из выходов . На рис. 3.2 также показаны: комбинации двоичных входов определяющие поразрядные значения чисел А и В; единичные значения функций возбуждения для 1-го и 2-го D-триггеров соответственно.

8. Как видно из кодированного графа переходов – рис. 3.2:

Нетрудно также получить функцию возбуждения

Функция V₂ содержит 8 минитермов. Попытаемся ее минимизировать. Для этого воспользуемся диаграммой Вейча — рис. 3.3, где тонкими овалами выделены группы минитермов, образующих простые импликанты. В результате минимиза­ции ФАЛ V₂ получаем

9. Взяв за основу микросхемы серии К155 (см. [6] или рис, 2.2), обеспечивающие реализацию полученных в п. 8 функций, получаем один из вариантов логической схемы искомого автомата – рис. 3.4. Здесь для обозримости схемы принят графический прием вложения всех соединений в некоторую гипотетическую магистраль (жирная линия на рис. 3.4) с установлением строгого соответствия между одинаково пронумерованными входами и выходами. Как видно из рис. 3.4, для реализации последовательного компаратора требуется 5 корпусов или кристаллов.

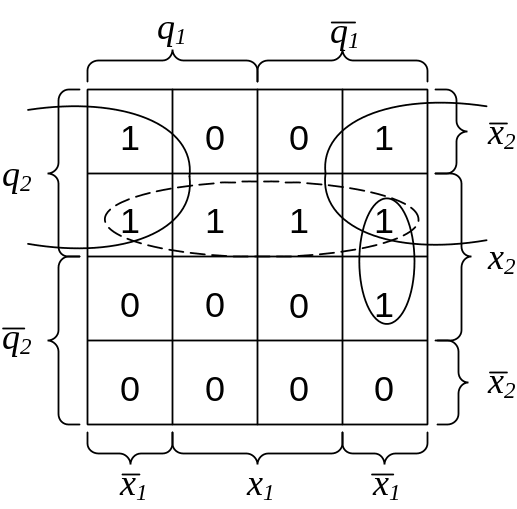
Рис. 3.3. Диаграмма Вейча для функции V₂

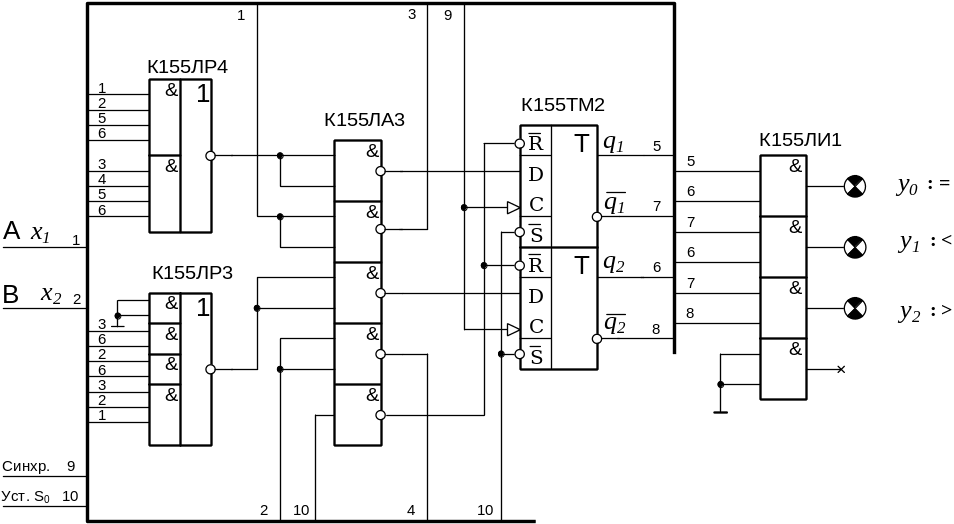
Рис. 3.4. Логическая схема компаратора (Вариант - 1)

10. Проверим возможность повышения качества синтеза за счет использования ПЛМ. Для реализации функций возбуждения необходимо пять вертикальных шин матрицы Ml (по общему числу минитермов). Выходную логику также выгодно вложить в ПЛМ. Для этого перейдем к автоматной модели Мили (рис. 1.2), принимая представленный на рис. 3.4 вариант кодирования состояний входных сигналов автомата. В соответствии с п. 5 раздела 3 убеждаемся в том, что функция в точности совпадает с функцией . В свою очередь каждая из функций содержит по 5 минитермов и после минимизации приобретает вид:

Для реализации всех полученных функций необходима ПЛМ со структурой , . В результате настройки ПЛМ на указанные функции получаем 2-й вариант логической схемы — рис. 3.5, который легко размещается на 2 кристаллах.

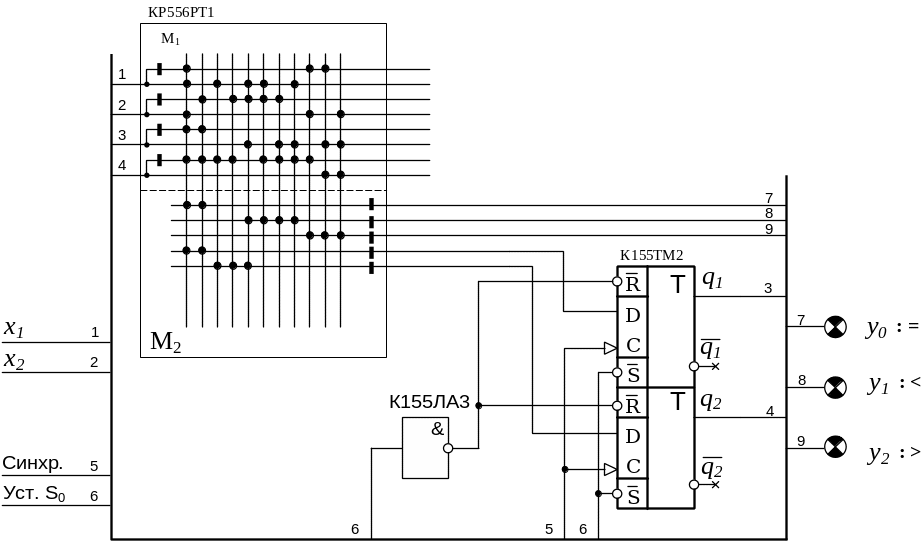
Рис. 3.5. Логическая схема компаратора (Вариант - 2)

Итак, мы раскрыли многие тонкости сквозного проектирования управляющего автомата с конечным числом состояний. Для того чтобы получить и обосновать Ваш проект управляющего автомата необходимо рассмотреть, по меньшей мере, 2 – 3 варианта его абстрактной и структурной реализации. Многоальтернативный синтез рекомендуется проводить с использованием пакета программ, именуемого SANAR [9] и разработанного студентами потока кафедры ВМСиС.