1.2. Предварительная обработка результатов наблюдений

Движение по дороге потока автомобилей представляет собой неустановившийся процесс, в котором взаимное расположение и скорости автомобилей постоянно меняются» Поэтому скоростной режим движения транспортного потока может быть охарактеризо­ван только средними статистическими показателями (математи­ческим ожиданием, дисперсией и др.).

Рассмотрим пример статистической обработки результатов измерений, используя для этой цели вариационный ряд величин скоростей движения (табл. 1.1) автомобилей, полученный при измерении радиолокационным прибором "Фара".

Таблица 1.1.

Статистический ряд скоростей движения автомобилей (км/ч)

34, 56, 52, 44, 62, 48, 42, 46, 44, 36, 48, 52, 49, 36, 42,

70, 40, 56, 38, 54, 60, 52, 44, 44, 50, 40, 44, 42, 60, 34,

46, 32, 40, 48, 64, 50, 44, 38, 46, 40, 54, 44, 38, 34, 28,

46, 44, 36, 34, 32, 34, 46, 44, 42, 32, 34, 54, 52, 60, 44,

58, 40, 42, 50, 68, 64, 34, 44, 42, 60, 58, 28, 42, 34, 40,

45, 40, 42, 46, 52, 54, 50, 52, 34, 48, 42, 40, 50, 38, 36,

44, 40, 48, 54, 50, 38, 50, 44, 34, 42

Статистическая обработка начинается с установления шкалы интервалов, в соответствии с которой группируются результаты наблюдений. Для определения оптимальной величины интервала h, воспользуемся формулой Стерджеса [ 8]:

(1.1)

где R - размах наблюдений;

V_max, V_min - соответственно максимальное и минимальное значение скорости в исследуемом вариационном ряду (cм. табл. 1.1);

N - общее число наблюдений»

Если h оказывается дробным числом, то за величину интервала следует взять либо ближайшее число, либо ближайшую несложную дробь. В рассматриваемом примере величина интер­вала

.

За величину интервала принимаем h = 5 км/ч.

За начало первого интервала а₁ рекомендуется прини­мать величину, равную (V_min - 0.5h), тогда а₂ = a₁ + h ; а₃ = a₂ + h. Построение интервалов продолжают до тех пор, пока начало следующего по порядку интервала не будет равным или большим V_max.

После установления шкалы интервалов приступают к группировке результатов наблюдений. Обычно все вычисления в математической статистике проводят в табличной форме, которая обладает наглядностью и позволяет проверять вычис­ления на каждом этапе. В первый столбец таблицы 1.2 заносят граница интервалов, а во второй - значения середин интер­валов V_ci.

При подсчете частот целесообразно использовать следую­щую методику [11]. Таблицу 1.1 просматривают по порядку от первой до последней строчки, и при чтении каждого ре­зультата соответствующую метку (черточку) заносят в тот класс, к которому относится данное наблюдение в рассматривае­мом примере, это будет значение скорости автомобиля, соответ­ствующее определенному интервалу скоростей. Каждый знак отвечает шести наблюдениям, поэтому подсчет частот облегча­ется. Определенные таким способом частоты попадания наблю­даемых параметров в соответствующие интервалы заносим в чет­вертый столбец табл. 1.2. В пятый и шестой столбцы табл.1.2 помещают значения частости и накопленной частости.

Таблица 1.2.

Построение интервального вариационного ряда

Границы интерва­лов скоро­стей дви­жения (αi - βi) км/ч	Середи­ны ин-терва­- ловVci, км/ч	Подсчет частот	Опыт­ные часто­ты	Опыт-ные часто-сти	Накоп- ленные опытные частости
1	2	3	4	5	6	7	8
25, 1-30	27,5	2	2	0,02	0,02	55	1512,5
30, 1-35	32,5	13	13	0,13	0,15	422,5	13731,25
35, 1-40	37,5	18	18	0,18	0,33	675	25312,5
40, 1-45	42,5	24	24	0,24	0,57	1020	43350
45, 1-50	47,5	19	19	0,19	0,76	902,5	42868,75
50, 1-55	52,5	11	11	0,11	0,87	577,5	30318,75
55, 1-60	57,5	8	8	0,08	0,95	460	26450
60, 1-65	62,5	3	3	0,03	0,98	187,5	11718,75
65, 1-70	67,5	2	2	0,02	1,00	135	9112,5
Итоговая строка			= =100	==1,0		=44,35	=204375

Частость (или относительная частость) - это отношение частоты, соответствующей рассматриваемому интервалу скоро­стей, к общему числу наблюдений.

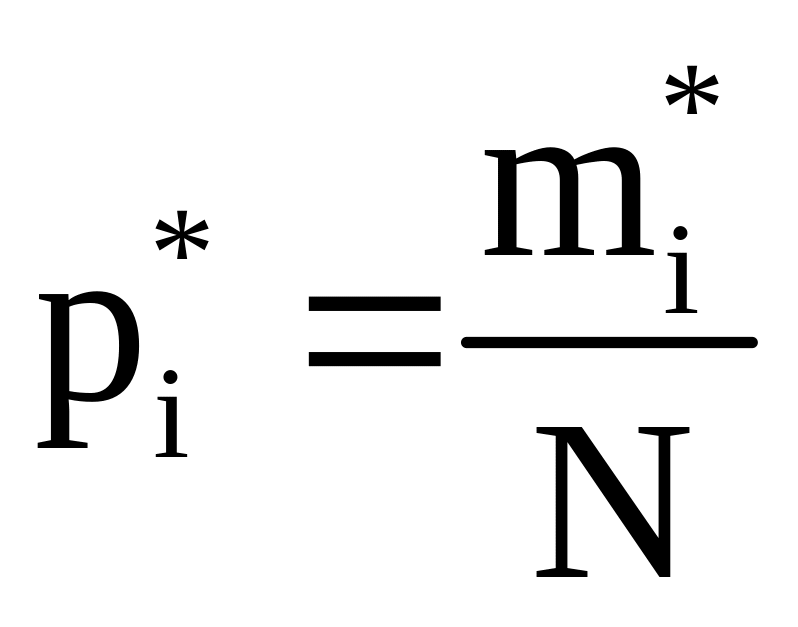(1.2)

Накопленная частость - это последовательная сумма частостей каждого интервала.

В седьмой и восьмой столбцы помечаются соответственно рассчитанные значения , , необходимые для последующих вычислений.

Величины , , и суммируются и наносятся в итоговую строку таблицы. По данным табл. 1.2 строят гисто­грамму, полигон и кумулятивную кривую, которые являются графическим изображением статистического ряда. Они позволяют в наглядной ферме представить основные закономерности изме­нения значений исследуемого параметра.

Гистограмма служит для изображения только интервального статистического ряда. Для её построения в прямоугольной си­стеме координат (рис. 1.2, а) по оси абсцисс откладываются отрезки, изображающие интервалы варьирования, и на этих отрезках, как на основании, строят прямоугольники с высотами, пропорциональными частостям соответствующего интервала. При построений гистограммы обязательно выполняется условие

где H_i - высоты прямоугольников гистограммы,

В результате получается ступенчатая фигура, состоящая из прямоугольника, которая и называется гистограммой.

Полигон служит, для изображения как дискретных, так и интервальных статистических рядов. Для его построения в пря­моугольной системе координат (рис, 1.2, а) наносят точки с координатами ( ; ), которые последовательно соединяют. Подученная ломаная линия называется полигоном.

Рис. 1.2. Графическое изображение результатов наблюдений за скоростями движения автомобилей: ее - кривая распределения, б - кумулятивная кривая

Кумулятивная кривая (кривая накопленных частостей) стро­ится следующим образом. В прямоугольной системе координат (рис. 1.2, б) по оси абсцисс откладываются интервалы, а по оси ординат, соответствующие им значения накопленной частости. Причем нижней границе первого интервала соответствует частость, равная нулю, а верхним - соответствующие значения накопленных частостей. Построив кумулятивную кривую, можно приблизительно установить число элементов ряда, для которых значение параметра меньше или равно заданному числу. Например, на кумулятивной кривой (рис. 1.2, б) показаны скорости движения, соответствую­щие 15, 50 и 85 % обеспеченности. Нижняя часть кривой примерно до 15 % обеспеченности показывает, с какой скоростью движутся наиболее медленные автомобили, вызывающие основную потребность в обгонах. Обеспеченность 50 % выражает среднюю скорость пото­ка. Её принимают за основную характеристику режима движения транспортного потока. Изгиб верхней части кривой примерно от 80-90 % обеспеченности выделяет наиболее быструю группу авто­мобилей, в число которых входят и автомобили, водители которых нарушают требования безопасности движения. Поэтому за наиболь­шую скорость движения автомобилей обычно принимают скорость 80 % обеспеченности, что является исходном при разработке мер по организации движения [2] .

Построение гистограммы, полигона и кумулятивной кривой представляет собой первый шаг при анализе статистического ряда наблюдений. Однако на практике этого часто бывает недостаточно, в особенности, когда необходимо сравнить два или более ряда.

Следует отметить, что сравнению подлежат только так называемые однотипные статистические ряды, т.е. ряды, полученные в результате сходных наблюдений. Однотипные, стати­стические ряды обычно имеют похожую форму при графическом изображении, но могут отличаться по средним значениям наблю­даемого параметра и показателям вариации. Средние величины и показатели вариации позволяют судить о характерных осо­бенностях вариационного ряда и называются статистическими характеристиками. К статистическим характеристикам относятся также показатели, характеризующие различия в скошенности полигонов и различия в их островершинности. Наиболее распространенной характеристикой является статисти­ческое среднее арифметическое или, выборочное среднее. Оно определяет центр распределения случайной величины и имеет ту же размерность, что и изучаемый параметр. Его значение определяется по формуле

, (1.3)

где Vc_i - центр интервала;

, - соответствующие, этому интервалу частоты и частости значений параметра;

N - общее число наблюдений ( N = ). Статистическое среднее арифметическое отвечает требова­ниям состоятельности, несмещенности и эффективности и, сле­довательно, его надлежит брать в качестве доброкачественной оценки для ожидаемого математического ожидания всей гене­ральной совокупности

. (1.3)

Для рассматриваемого примера, используя данные седьмого столбца табл. 1.2, среднее значение скорости автомобилей в транспортном потоке:

.

Показатели вариации характеризуют рассеяние результатов наблюдений вокруг средней величины. В качестве меры рассеяния обычно используют дисперсию и среднее квадратичное отклоне­ние.

Статистической или выборочной дисперсией D^* называ­ется средняя арифметическая квадратов отклонений параметра от его средней арифметической

(1.5)

Для расчетов статистической дисперсии удобно использо­вать следующую формулу:

Мера рассеяния должна выражаться в тех же единицах, что и наблюдаемый параметр, поэтому вместо дисперсии в качестве показателя вариации чаще используется статистическое среднее квадратичное отклонение, которое определяется как корень квадратный из дисперсии

. (1.6)

В качестве несмещенной оценки дисперсии D генеральной совокупности используют выражение

и, значит, исправленное несмещенное среднее квадратическое отклонение (т.е. его оценка)

(1.7)

В литературе [8] часто вместо выражения "исправленное среднеквадратическое отклонение" используют термин "стандарт­ное отклонение". Найдем по формулам (1.6) и (1.7) с помощью данных табл. 1.2 статистическое среднеквадратическое и стандартное отклонения:

.

.

Для характеристики того, насколько средняя арифметическая хорошо представляет статистический ряд, используется коэф­фициент вариация, равный выраженному в процентах отношению стандартного отклонения к средней арифметической:

. (1.8)

Чем меньше коэффициент вариации, тем меньше среднее рассеяние значений параметра вокруг средней арифметической. Если срав­нивают два статистических ряда, имеющих одинаковые средние арифметические, то средняя арифметическая ряда с меньшим коэффициентом вариации более представительна. Если коэффициент вариации υ < 33 %, то можно проводить про­верку о нормальности-распределения [11]. В нашем примере коэффициент вариации

.

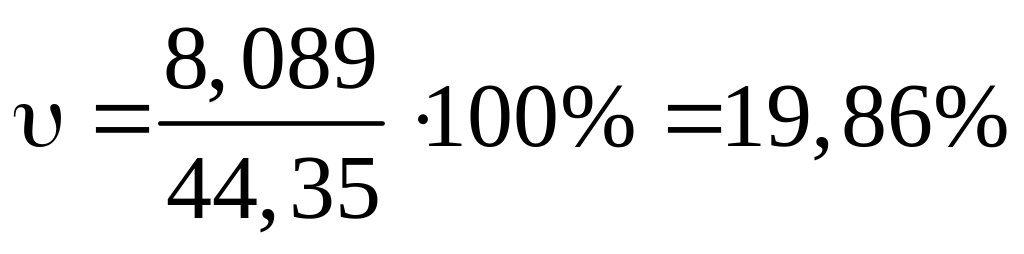Асимметрия и эксцесс дают дополнительную информацию о форме случайной величины. Эксцесс или островершинность E_к характеризует отклонение по вертикали полигона статистического ряда от кривой нормального распределения. Асимметрия или скошенность A_s характеризует смещение влево или вправо вер­шины полигона распределения по отношению к нормальной кривой. Для расчета асимметрии и эксцесса применяются следующие фор­мулы:

;

.

В рассматриваемом примере

А_s = 0,53; Е_к = - 0,263 .

Для симметричного распределения A_s = 0. Если A_s > 0, как в данном примере, то имеем левостороннее распределение, при отрицательном значении асимметрии - распределение правосторон­нее.

Для нормального распределения Е_к = 0. Поэтому, если эксцесс некоторого распределения отличается от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и "острую" вершину, чем нормальная кривая; если эксцесс отрицательный, как в рассматриваемом примере, то сравниваемая кривая имеет более низкую и "плоскую" вершину, чем нормальная кривая.