
- •Векторні функції скалярного аргументу і їх властивості
- •Границя векторних функцій
- •Tеорема:
- •Доведення:
- •Неперервність векторних функцій
- •Векторна похідна
- •Елементи тригранника Френе
- •Дотична до кривої
- •Теорема:
- •Доведення:
- •Нормальна площина кривої
- •Бінормаль кривої
- •Спрямна площина
- •Головна нормаль
- •Довжина дуги кривої Натуральна параметризація
- •Кривизна кривої
- •Теорема:
- •Доведення:
- •Натуральні рівняння кривої
- •Формули Френе
- •Доведення:
- •Плоскі криві
- •Лінія на поверхні
- •Дотична площина і нормаль до поверхні
- •Перша квадратична форма поверхні
- •Застосування першої квадратичної форми
- •Друга квадратична форма поверхні
- •Кривизна кривої на поверхні Нормальна кривизна поверхні Теорема Меньє
- •Теорема Меньє
- •Нормальна кривизна поверхні в даному напрямку є величина стала.
- •Геодезична кривизна і її обчислення
- •Головні кривизни на поверхні
- •Індикатриса кривизни Дюпена
- •Класифікація точок на поверхні:
- •Класифікація точок на основі поняття ідекатриси Дюпена
- •Класифікація точок поверхні на основі поняття Гаусової (повної) кривизни поверхні
- •Класифікація точок з використанням поняття стичного параболоїда поверхні
- •Поверхня обертання і її рівняння
- •Головні напрямки на поверхні
- •Асимптотичні напрямки на поверхні Асимптотичні лінії
- •Геодезичні напрямки на поверхні
- •Сферичне зображення області на поверхні Теорема Гауса
- •Теорема :
- •Ізометричні поверхні Згинання поверхні
- •Теорема Гауса-Бонне(без доведення)
- •Теорема Гауса-Бонне:
- •Топологічний простір
- •I. Об'єднання будь-якої кількості (скінченної або нескінченної) відкритих множин є відкрита множина.
- •II. Перетин будь-яких двох відкритих множин є відкрита множина.
- •Топологічні перетворення і їх властивості
- •Замкнені множини Граничні точки
- •3°. Перетин будь-якої системи (скінченої чи нескінченної) замкнених множин є замкнена множина.(якщо - сукупність замкнених множин, то множина замкнена).
- •4°. Множина м простору замкнена тоді і тільки тоді, коли вона містить всі свої граничні точки.
- •Кліткове розбиття поверхні Орієнтовні поверхні
- •Теорема Ейлера для многогранників
- •Приклади топологічно правильних многогранників
- •Топологічні властивості проективної площини
Нормальна площина кривої
Нормальною площиною кривої,в даній точці, називається площина, яка проходить через дану точку кривої, перпендикулярно до дотичної.

(умови існування ті самі що і для дотичної)
Знайдемо рівняння нормальної площини: (1)
дано криву лінію і т.Р, візьмемо на площині довільну точку М
![]()
Р0М
належить нормальній площині, а площина
перпендикулярна до дотичної,тому
![]() ,
тобто
,
тобто
![]()
![]() (3)
–
векторно-параметричне рівняння площини
(3)
–
векторно-параметричне рівняння площини
Якщо площина задана параметрично (4)
нехай біжуча т.М (x,y,z), тому і
![]()
з рівності (3) маємо:
![]()
загальне рівняння нормальної площини
Стична площина кривої і її рівняння
Р озглянемо
у просторі криву лінію задану рівнянням
(1)
озглянемо
у просторі криву лінію задану рівнянням
(1)
нехай Q- нескінченно близька до т.Р
відстань
![]()
відстань
від т.Q
до площини
![]() ,
,
![]()
|e|=1- одиничний вектор
Стичною площиною кривої (1) в т.Р називається площина, яка проходить через т.Р, кривої, і для якої виконується така умова:
 (2)
(2)
Теорема:
Всяка регулярна,принаймні двічі неперервно-диференційовна, крива у кожній своїй точці має стичну площину, яка є єдиною.
Або всяка площина, що містить дотичну є стичною площиною кривої.
якщо
,
векторна параметризація кривої, то
стична площина в т.Р паралельна до
векторів
![]()
Доведення:
Нехай площина Р є стичною, тому для неї виконується рівність (2). Скористаємось нею для доведення, для цього визначимо h і d
![]()
Для знаходження h розглянемо скалярний добуток
![]()
![]()

Звідси
![]() ,
отже
,
отже
![]() і
і
![]() належать одній площині.
належать одній площині.
Покажемо, що всяка площина, яка проходить через т.Р, кривої (1), паралельно до векторів і є стичною, тобто виконується умова (2):
 , тому
що
, тому
що
![]()
Знайдемо рівняння стичної площини для різних способів її параметризації:
1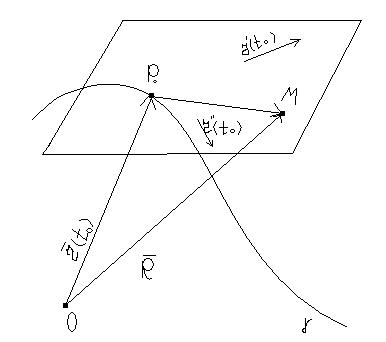 )
Нехай лінія задана векторним рівнянням
(1)
)
Нехай лінія задана векторним рівнянням
(1)
нехай т.М - довільна точка стичної площини
![]()
З
![]()
вектори лежать в одній площині, отже є компланарними, лінійно залежними.
виразимо вектор через інші вектори:
![]()
![]() (3) -
векторно-параметричне рівняння
(3) -
векторно-параметричне рівняння
оскільки вектори компланарні, то:
![]()
(![]() 4)
– векторно-параметричне рівняння
4)
– векторно-параметричне рівняння
2)
Нехай
задане параметричне рівняння:
![]()
в
т.Р0
,
![]()
тоді із рівності (3):
![]() (5)
- параметричне
рівняння стичної площини
(5)
- параметричне
рівняння стичної площини
із
(4) маєм
![]() (6)
(6)
– канонічне рівняння стичної площини
3) =>
![]()
![]()
![]()
- параметричне рівняння стичної площини
![]() -
канонічне
рівняння стичної площини
-
канонічне
рівняння стичної площини
4) Нехай лінія задана рівнянням:
напишемо рівняння стичної площини в т.(x0,y0,z0)
нам
потрібно знайти вектори
![]()
припустимо,що
,
отримаєм
![]()
![]() (*)
(*)
припустимо,
що одне із
![]() відоме, нехай
відоме, нехай
![]() =а.
Отримаємо тоді систему двох рівнянь, з
якої і визначимо
=а.
Отримаємо тоді систему двох рівнянь, з
якої і визначимо
![]() ,
рівність (*) продиференціюємо по t:
,
рівність (*) продиференціюємо по t:
![]()
в
останній рівності замість
підставимо їх значення і припустимо,
що
![]() ,
отримаємо систему з двома невідомими,
розв’язавши її отримаємо
,
отримаємо систему з двома невідомими,
розв’язавши її отримаємо
![]() , далі напишемо рівняння стичної площини.
, далі напишемо рівняння стичної площини.
