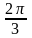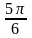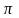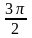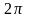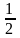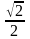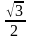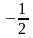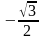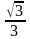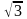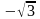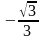Немає жодної сфери математики, яка

коли – не будь не знайде застосування

для вивчення явищ реального світу

М.І.Лобачевський

Радіанна та градусна міра кута. Тригонометричні функції числового аргументу. Співвідношення між тригонометричними функціями одного і того ж аргументу

Історія тригонометричних функцій.

Вавілоняни вже на початку III тисячоліття до н.е. мали календар з розподілом року на 12 місяців. Отже вони вміли визначати положення сонця і зірок на небосхилі, тобто володіли певними знаннями тригонометричного характеру.

Велике значення для розвитку тригонометрії в період її зародження мали праці грецьких учених.

Протягом тисячі років тригонометрія була підсобною наукою у астрономії.

Складалися нові таблиці, знаходилися нові залежності між тригонометричними функціями, за допомогою яких розв’язувалися складні задачі, але тригонометрія залишалася тільки частиною астрономії, самостійної науки не існувало.

Наприкінці ХV ст. італійський мандрівник Христофор Колумб відкрив узбережжя Америки. Слідом за ним туди зробив кілька подорожей інший італієць – Америго Віспуччі. Португалець Васко да Гама відкрив морський шлях на Індію. Незабаром кораблі Магеллана вперше в історії зробили навколосвітню подорож. Почалася епоха великих географічних відкриттів, завоювань нових територій, освоєння незліченних багатств нових земель.

Не тільки окремі групи купців і мореплавців, але і цілі держави боролися за право експлуатації нових земель. Потрібні були більш потужні і швидкохідні судна, точні географічні карти, досконалі способи орієнтування в відкритому океані.

Все це і багато чого іншого привело до необхідності розвивати астрономію – науку про рух небесних тіл, а розвиток астрономії був неможливий без розвитку тригонометрії.

Перші кроки тригонометрії

Слово “тригонометрія” складається із двох грецьких слів: “триганон” – трикутник і “метрайн” – вимірювати. У буквальному значенні “тригонометрія” означає “вимір трикутників”.

Астрономія, а разом з нею і тригонометрія виникли і розвивалися в народів з розвиненою торгівлею і сільським господарством: у вавілонян, греків, індійців, китайців. Зародилася вона багато століть тому. Про це ми можемо не тільки здогадуватись.

В одному з китайських рукописів, що був написаний близько 2637 року до н.е., є відомості з астрономії, де застосовуються обчислення тригонометричного характеру.

Внесок Ейлера в тригонометрію.

Завершальний етап у розвитку тригонометрії пов'язаний з ім’ям Леонарда Ейлера.

Заняття астрономією, географією і морехідними науками неможливі без застосування тригонометрії. Але до початку XVIII ст. вона була наукою неопрацьованою, часто незручною в роботі, що іноді призводило до помилок через плутанину в знаках тригонометричних функцій у різних чвертях кола. Кожна формула виводиться з креслення і всі міркування записувалися словесно. Це змусило Ейлера переглянути доведення тригонометричних формул. Він упорядкував питання про знаки тригонометричних функцій у різних чвертях, ввів однакове позначення сторін трикутника: а, в, с і протилежних кутів А, В, С.

Ейлер розробив тригонометрію як науку про тригонометричні функції, запропонував розглядати тригонометричні функції як числа, що виражають відношення відповідних тригонометричних ліній до радіуса кола.

У працях Ейлера тригонометрія набула сучасного вигляду. На підставі його робіт були укладені підручники з тригонометрії, що викладають її в строгій науковій послідовності.

Вища математика.

Комплексні числа

Диференціальні рівняння

Аналітична геометрія

(реалізація міжпредметних зв’язків- метод логічної градації)

Геометрія.

Розв’язування трикутників Розв’язування прямокутних

трикутників

Математика

Тригонометричні функції числового аргументу.

Фізика.

Гармонійні коливання

Динаміка

Оптика

Астрономія.

Астрономічні дослідження

Тригонометричні функції означені у курсі математики як функції кута. Водночас різні задачі з математики, фізики, економіки та інших наук приводять до тригонометричних функцій, аргументами, яких є не кути, а інші величини (довжина, час, температура тощо). Тому в математиці тригонометричні функції розглядають як функції числового аргументу, які в першу чергу використовують для опису різноманітних періодичних процесів.

Періодичними називаються процеси, для яких характерним є повторюваність подій, значень розглядуваних величин. Схід та захід Сонця, коливання маятника, обертальний рух колеса, заповнюваність міського транспорту – все це приклади періодичних процесів. Відповідно, періодичними називаються функції, які повторюють свої значення через певні проміжки зміни аргументу.

1. Одиничне коло. Радіанна та градусна міра кута. Формули переходу від градусної міри до радіанної і навпаки.

Градусна міра кута

Ще в Древньому Вавілоні за довго до нашої ери жерці вважали, що свій денний шлях сонце проходить за 180 кроків, а значить один крок складає 1/180 розгорнутого кута.

У Вавилоні була прийнята шестидесятирічна система числення, тобто фактично числа записувались у вигляді суми степенів числа 60, а не 10.

Тому зрозуміло, що для більш мілких одиниць вимірювання кутів один “крок” послідовно ділиться на 60 частин. А саме слово “градус” походить від латинського gradus (крок, сходинка). Секунда перекладається як “друга”.

Р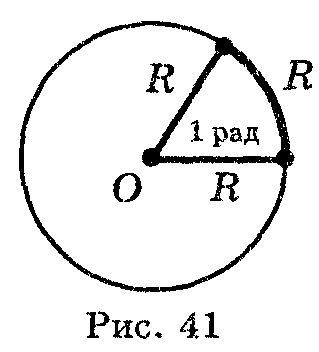 адіанна міра кута

Крім градусної міри, використовуються і інші одиниці вимі­рювання кутів. У математиці і фізиці це радіанна міра кута.

1 радіан – центральний кут, який опирається на дугу, довжина якої дорівнює радіусу (рис.1).

У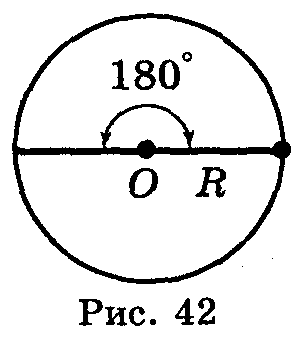 становимо зв’язок між радіанним і градусним вимірюванням кутів. Куту, що дорівнює 180°, відповідає півколо, тобто дуга, довжина якої дорівнює πR. Щоб знайти радіанну міру кута в 180°, треба довжину дуги πR розділити на довжину радіуса R: 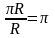. Отже, радіанна міра кута в 180° дорівнює π: 180°=π рад. Із цієї формули одержуємо (розділивши ліву і праву частини рівності на 180):

1° = 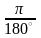рад, або 1° 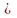0,017 рад.

Із рівності 180°=π рад також одержуємо (розділивши ліву і праву частини рівності на π):

1рад= , або 1рад 57°.

Розглянемо приклади переходу від радіанної міри до градусної і навпаки.

Приклад 1. Виразіть в радіанах величини кутів 30°; 45°; 60°; 90°.

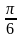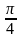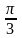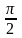Розділивши ліву і праву частини рівності: 180°=π рад послідовно на 6, 4, 3, 2, одержуємо: 30°= рад, 45°= рад, 60°= рад; 90°= рад.

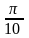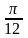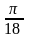Приклад 2. Виразіть в градусах величини кутів рад, рад, рад, рад.

Р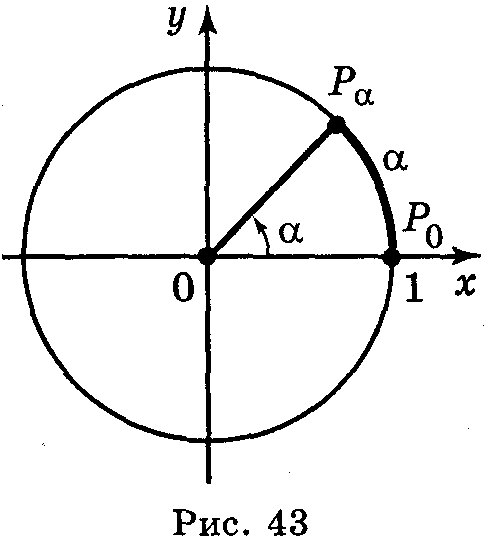 озділивши ліву і праву частини рівності: 180°=π рад послідовно на 10; 5; 12; 18, одержуємо: рад=18º; рад=36º; рад=15º; рад=10º.

Одиничне коло

Розглянемо на координатній площині коло радіуса 1 з центром у початку коорди­нат, яке називається одиничним. Позначимо точку Р_о – правий кінець горизонтального діаметра. Поставимо у від­повідність кожному дійсному числу α точку кола за такими правилом:

1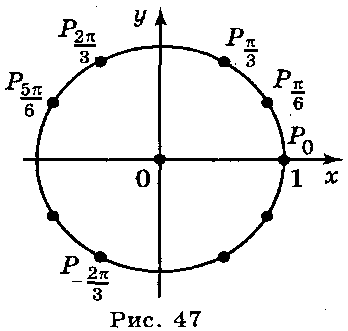 ) Якщо α>0, то, рухаючись по колу із точки Р_о в напрямі проти годинникової стрілки (додатний напрям обходу кола), опишемо по колу шлях довжи­ною а, кінцева точка цього шляху і буде шуканою точкою Ρ_α.

2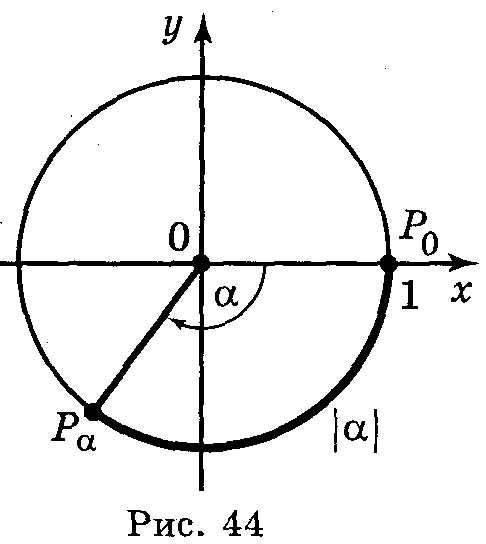 ) Якщо α<0, то, рухаючись із точки Ρ_о в напрямі за годинниковою стрілкою, опишемо по колу шлях дов­жиною |α|; кінець цього шляху і буде шукана точка Р_α.

3) Якщо α=0, то поставимо у відповідність точку Р_о.

Таким чином, кожному дійсному числу можна поставити у відповідність точку Ρ₀ одиничного кола.

Якщо α=α_о+2πk, де k – ціле число, то при повороті на кут α одержуємо одну і ту саму точку, що й при повороті на кут α_о.

2. Означення тригонометричних функцій ДЧА. Знаки на чвертях.(Методи: пояснення, ілюстрації, інформаційно - комунікативний)

Синусом кута називається відношення ординати точки Р_α(х;у) кола до його раді­уса: .

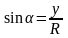Косинусом кута називається відношення абсциси точки Р_α(.х;у) кола до його радіуса: .

Тангенсом кута називається відношення ординати точки Р_α(х;у) до її абсциси: .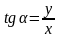

Котангенсом кута називається відношення абсциси точки Р_α(х; у) до її ординати: .

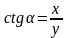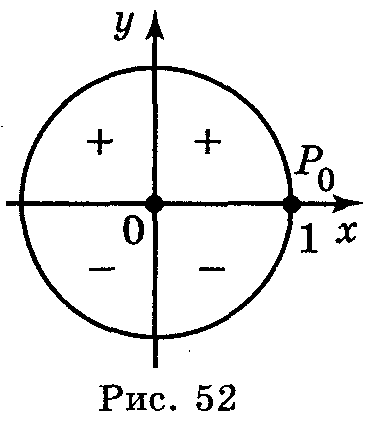
Знаки синуса, косинуса в чвертях:

Тангенсом числа α називається відношення синуса числа α до його косинуса: .

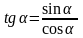Тангенс визначений для всіх а, крім тих значень, для яких cosα=0, тобто, α= +πn, n Ζ.

Д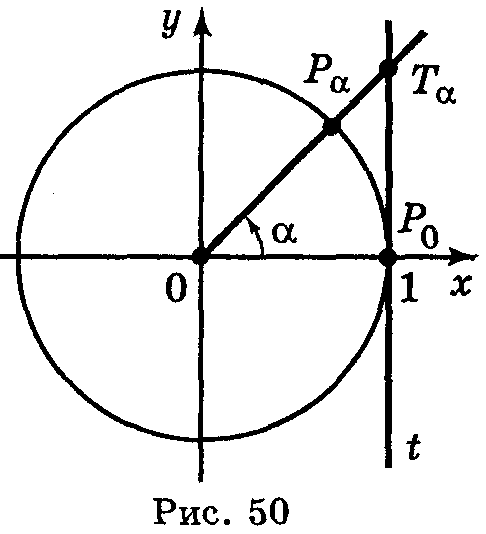 ля розв'язування деяких задач корисно мати уявлення про лінію тангенсів. Проведемо дотичну t до одиничного кола в точці Ρ_о. Нехай α – довільне число, для якого cosα 0, тоді точка Р_α (cosα; sinα) не лежить на осі ординат і пряма ОР_α перетинає t в деякій точці Т_α з абсцисою 1. Знайдемо ординату точки Т_α із трикут­ника ОР_оТ_α.

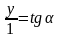; у=tgα.

Таким чином, ордината точки перетину прямих ОР_α і t дорівнює тангенсу числа α. Тому пряму t нази­вають віссю тангенсів.

К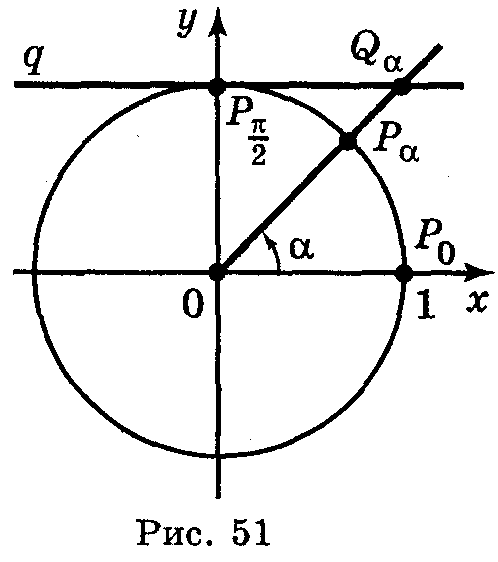 отангенсом числа α називається від­ношення косинуса числа α до його синуса: .

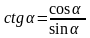Котангенс визначений для всіх α, крім таких значень, для яких sin α 0, тобто, a = π n, n Ζ.

Введемо поняття лінії котангенсів. Проведемо дотичну q до одиничного кола в точці . Для довільного числа α, якщо sin α 0 і відповідно точка Р_α (cos α, sin α) не лежить на осі ОХ і тому пряма ОР_α перетинає пряму q у деякій точці Q_α з ординатою, що дорівнює 1. Із трикутника О Q_α маємо: 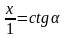, звідси х = ctg α. Таким чином, абсциса точки перетину прямої ОР_α і q дорівнює котангенсу числа α, тому пряму q називають віссю котангенсів.

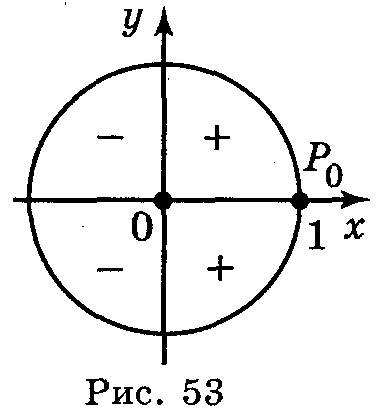
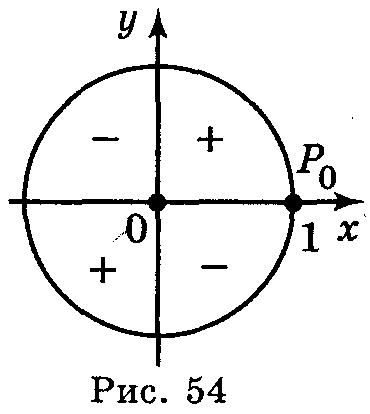
Знаки тангенса і котангенса в чвертях:

П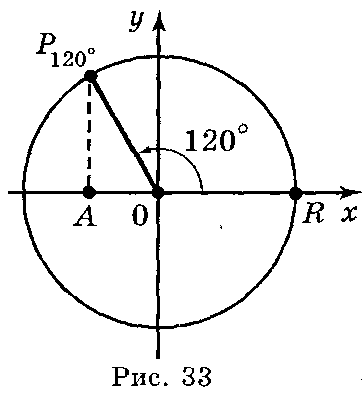 риклад 1. Знайти sin α, cosα, tgα, ctgα, якщо α=120°.

Побудувавши точку Р_120º, маємо (рис. 33):

; ; ; ;

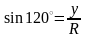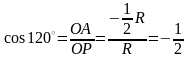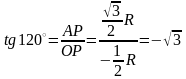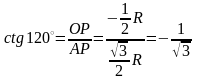Я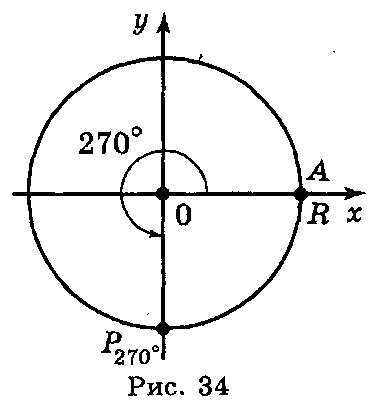 кщо будь–який кут розглядати як фігуру, утворену обертанням променя навколо своєї початкової точки у двох можливих напрямах (додатному – проти годинникової стрілки, від'ємному – за годинниковою стрілкою), то дане визначення можна використовувати для будь–яких кутів.

Приклад 2. Знайти sinα, cosα, tgα, ctgα, якщо α=270°.

При повороті на 270° навколо точки О радіус ОА перейде в радіус ОР, тоді (рис. 34)

Р_270º·(0;–R ) і, отже, sin270°=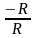 =–1, cos270°=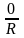 =0, ctg270°=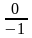 =0 , tg270° не має змісту.

Із курсу геометрії відомо, що величина кута в градусах виражається числом від 0° до 180''. Кут Повороту може виражатися в градусах, яким завгодно дійсним числом від –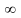 до + .

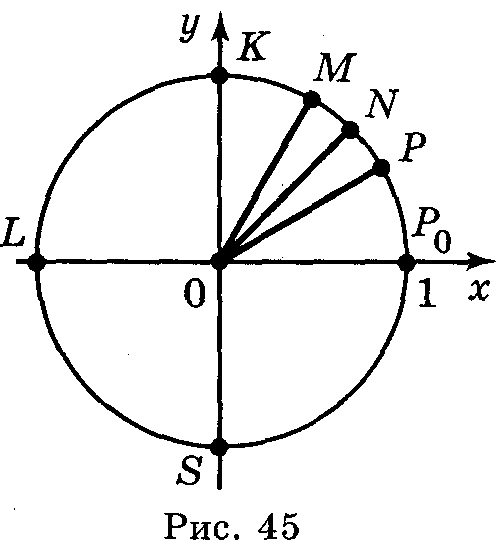
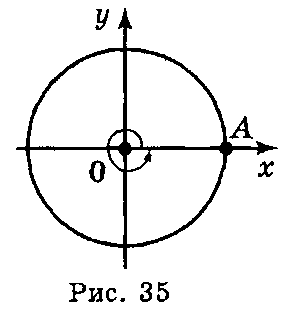
Приклад 3. Якщо початковий радіус ОА зробив повний оберт проти годинникової стрілки, то кут повороту буде дорівнювати 360° (рис. 35).

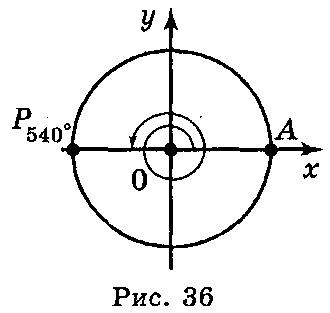
Якщо початковий радіус ОА зробив півтора оберти проти годинникової стрілки, то кут повороту буде дорівнювати 540º (рис. 36).

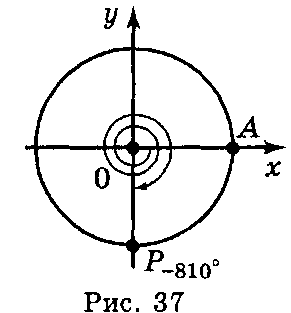
Якщо початковий радіус ОА зробив два повних оберти і чверть оберту за годинниковою стрілкою, то кут повороту буде дорівнювати 2 (–360°)–90°=–810° (рис. 37).

3 Таблиця значень тригонометричних функцій для деяких кутів(самостійна робота)

, гр	0	30	45	60	90	120	135	150	180	270	360
, рад	0
sin	0				1				0	-1	0
cos	1				0				-1	0	1
tg	0		1		–		-1			–
ctg	–		1		0		-1		–		–

4. Співвідношення між тригонометричними функціями одного і того ж аргументу( Метод: пояснення, ілюстрація, доведення формул)

Д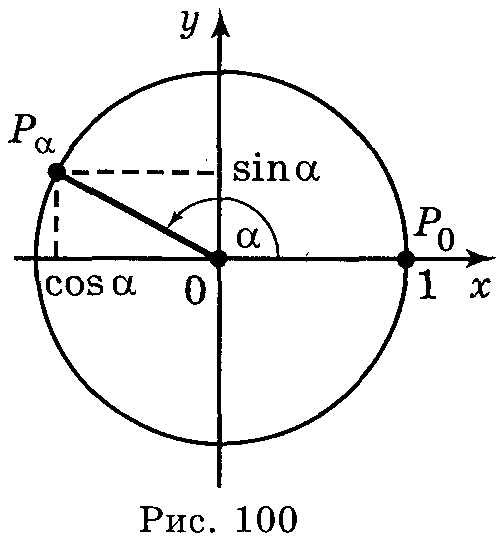 уже часто при розв'язуванні задач виникає проблема: зна­йти значення тригонометричних функцій, якщо задано лише зна­чення однієї з них. Отже, на сьогоднішньому занятті ми повинні згадати формули (залежності), які пов'язують тригонометричні функції одного і того самого аргументу.

1. Співвідношення між синусом і косинусом.

Нехай точка Ρ_α(х, у) одиничного кола отримана поворотом точки Р₀(1; 0) на кут α радіан, тоді згідно з означенням синуса і косинуса: х=cosα, у=sinα

Оскільки точка Р_α(х;у) належить одиничному колу, то координати (х; у) задовольняють рівнянню х +у²=1. Підставивши в це рівняння замість х і у значення cos α і sin α , отримаємо:

(cosα)²+(sinα)²=1

або (враховуючи, що (cosα)²=cos²α, (sinα)²=sin²α)

cos²α+sin²α=1.

Ця рівність називається основною триго­нометричною тотожністю.

З основної тригонометричної тотожності можна виразити sinα через cosα і навпаки:

, .
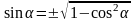
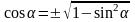