
Раздел 1 – программно-методические вопросы:
Цель статистического наблюдения
Объект статистического наблюдения
Единица наблюдения
программа наблюдения
проект формуляра
инструкции
источники информации
способы сбора данных
Раздел 2 – организационные вопросы:
Органы наблюдения
Срок наблюдения
Критический момент
Место проведения
Составление списков единиц совокупности
Расстановка и подготовка кадров адресаты
Критический момент – дата и время, по состоянию на которые сообщаются сведения. Срок наблюдения – период выполнения работы.
Материально-техническое снабжение для сбора, накопления, обработки, анализа и хранения информации.
43. Правило сложения дисперсии, и ее использование в экономическом анализе
Правило сложения дисперсий определяется так: общая дисперсия равна сумме величин межгрупповой дисперсии и средней из внутригрупповых дисперсий.
Следствие:
ŋ² = β²/ G² - коэффициент детерминации
ŋ = √ŋ² - корреляционное отношение
Коэффициент детерминации характеризует долю колеблемости, зависящую от изменчивости группировочного признака, а корреляционные отношение, меняясь от 0 до1 характеризует тесноту связи между изменчивостью группировочного признака и вариацией результативного.
44. Индексы средних величин.
Индексы средних величин – структурные индексы, их отличительный признак – объект анализа, изучается изменение средней величины (средней цены, средних затрат, средней производительности труда), а так как изучаются средние, то априори утверждается, что изучается качественно однородный массив, так как средняя считается типичной характеристикой только для качественно однородных массивов. Элементы анализа – различные объекты, что определяет сложность совокупности. Например, заказ на производство изделия различно на различных фирмах. Условия производства не могут совпадать, они варьируют , что определяет различный уровень себестоимости одного и того же изделия А на разных фирмах, а изменение среднего уровня себестоимости определяется во первых изменением уровня себестоимости на каждой отдельной фирме и тем сколько изделий они произвели и как изменился объем этих изделий. Такие ситуации анализируются с помощью структурных индексов.
В состав структурных индексов входят:
общие индексы переменного состава
общие индексы постоянного (фиксированного) состава
общие индексы структурных сдвигов
Схема построения структурных индексов * x – меняется, f – постоянная
I`x =`x₁ /`x₀ = (∑x₁f₁ / ∑f₁) / (∑x₀f₀ / ∑f₀)
Отражает изменения за счет x и f одновременно * x – меняется, f – постоянная
Ix = (∑x₁f₁ / ∑f₁) / (∑x₀f₁ / ∑f₁)
Отражает изменения только за счет x * x – не меняется, f – меняется
Ix(cр.сдв) = (∑x₀f₁ / ∑f₁) / (∑x₀f₀ / ∑f₀)
Отражает изменения за cчет f
I`x / I x = I x(cр.сдв)
По преведенной модели рассчитывают индекс цены, где x - это p, f – это q, индекс себестоимости, где x – z, а f – q
Важнейшим условием применения седних индексов является убежденность в том, что анализируются качественно однородные массивы.
45.
Стохастическая связь – связь между величинами, при которой зависимая переменная Y реагирует на изменение независимой переменной X или Xi изменением закона распределения. При стохастической связи зависимая переменная подвержена влиянию как рассматриваемых, т.е. учтенных зависимых переменных, так и влиянию неучтенных факторов.
Значение зависимой переменной имеет вероятностный характер. Стохастические связи проявляются только во всей совокупности и не проявляются в отдельных явлениях, следовательно стоханистические модели основы на положениях закона больших чисел.
Моделирование стоханистических связей
корреляционные
регрессивные
Корреляционная связь – существует там, где взаимосвязанные явления зависят только от случайных величин. Изменения факторных признаков вызывает изменение средней величины результативного признака.
Задача корреляционного анализа – изменение тесноты связи между варьирующими признаками с помощью коэффициентов и индексов корреляции. Методика их расчета зависит от количества учитываемых факторных признаков, поэтому коэффициенты, измеряющие тесноту связи, могут быть коэффициентами множественной корреляции.
Задачи регрессионного анализа – выбор типа модели, установление степени влияния независимых на зависимые переменные и определение расчетных значений зависимой переменной. Формально корреляционные связи, измеренные с помощью корреляционного анализа, измерение с помощью коэффициентов определения тесноты, регрессии. Показатели используются независимо, но полный анализ предполагает их совместное использование
Форма результата:yx = 10+2x (регрессионная модель), r = -0.75, Fэ>Fт
r – линейный коэффициент парной корреляции -1≤r≤+1
r = -0.75 – тесная обратная зависимость
46. Вторичная группировка
Вторичная группировка, или перегруппировка сгруппированных данных применяется для лучшей характеристики изучаемого явления (в случае, когда первоначальная группировка не позволяет четко выявить характер распределения единиц совокупности), либо для приведения к сопоставимому виду группировок с целью проведения сравнительного анализа.
Вторичная группировка - операция по образованию новых групп на основе ранее осуществленной группировки.
Применяют два способа образования новых групп. Первым, наиболее простым и распространенным способом является изменение (чаще укрупнение) первоначальных интервалов. Второй способ получил название долевой перегруппировки и состоит в образовании новых групп на основе закрепления за каждой группой определенной доли единиц совокупности.
47. статистическая сводка
статистическая сводка
обработка первичных материалов статистического наблюдения с целью их обобщения, заключающаяся в группировке, подсчете итогов, расчете статистических показателей, составлении статистических таблиц и др.
Статистическая сводка – систематизация единичных фактов, позволяющая перейти к обобщающим показателям. В широком смысле стат. сводка – это систематизация путем группировки, подсчет обобщающих характеристик и итогов, предоставление результатов в виде таблиц. В узком понимании – подсчет общих и групповых итогов.
Основные этапы сводки:
формулировка задач, ради которых выполняется сводка и группировка
формирование групп и подгрупп по выбранному экономистом признаку
контроль полноты и качества информации
В зависимости от уровня работы (макро-, микро-) сводка может быть децентрализованной и централизованной. В компьютерных сетях, на рабочем месте. На макроуровне – работают только в компьютерных технологиях.
48. Оценка выбора и параметров уравнения тренда
Основная тенденция (тренд) показывает, как воздействуют систематические факторы на уровень ряда динамики, а колеблемость уровней около тренда служит мерой воздействия остаточных факторов. Ее можно найти по формуле среднего квадратического отклонения:
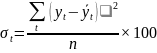
где уt, - исходный уровень ряда;
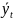 -
выравненный
уровень ряда.
-
выравненный
уровень ряда.
Этот показатель является оценкой адекватности статистической модели и называется стандартизированной ошибкой аппроксимации.
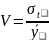
где
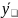 -средний
уровень ряда.
-средний
уровень ряда.
Для выбора типа уравнения тренда выше было предложено использовать показатели ряда динамики. Для проверки постоянства того или иного показателя ряда динамики целесообразно использовать статистические гипотезы. Для проверки существенности различий между показателями ряда достаточно разбить этот ряд на три части и рассчитать факторную и остаточную дисперсии. Далее необходимо воспользоваться критерием Фишера.
Относительной мерой колеблемости является коэффициент вариации
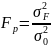
Если расчетное значение критерия больше табличного (Fр > Ft), то расхождения между показателями ряда могут считаться существенными. Такой подход может быть использован для таких показателей ряда динамики, как абсолютные темпы прироста, темпы роста и прироста, темпы наращивания.
Для оценки точности замены ряда динамики уравнением тренда используется оценка погрешности, которая определяется по формуле:
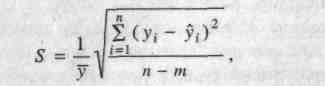
где. yi и €- фактические и расчетные значения уровней ряда динамики;
п - число уровней ряда;
т - число параметров в уравнении тренда;
- среднее значение уровня ряда.
49. статистические таблицы и графики.
Статистические таблицы – форма концентрированного изложения результатов
сводки и группировки. Может использоваться как аналитический инструмент и как форма изложения стат. данных.
Название
Шапка
А 1 2 3 4
Строки
Графы
Каждая таблица имеет подлежащее и сказуемое, подлежащее – объект, который описывается, чаще всего это первая графа таблицы. Подлежащее может быть простым, сгруппированным, комбинированным. Этим определяется тип таблицы (простая, комбинированная, групповая). Сказуемое разрабатывается как система показателей и помещается в графах.
Атрибуты статистической таблицы:
полное название
название всех граф с указанными единицами измерения
итоговые строки и столбцы.
Надо знать правила указанных единиц измерения и правила переноса таблиц.
Виды таблиц:
Простая
Простая перечневая
Простая территориальная
Хронологическая простая
Групповые
Комбинированная
Сложная таблица
Статистические Графики
Диаграммы а) Линейные б) Столбиковые в) Секторные д) Фигурные е) Ленточные |
Картограмма и картодиаграмма |
Линейные
Ленточные.
Среднегодовое производство зерна в Бангладеш по пятилеткам (млн. тонн).
Столбиковые (сравнительные).
Секторная (структура).Основные направления использования финансовых средств, %
Картодиаграмма. Площадь пахотных земель (по крупным землепользователям).
Картограмма.
50. Методы вычисления дисперсии
Расчет дисперсии. Дисперсию следует рассчитывать по методикам, которые объединяют расчеты средних величин и показателей вариации. Дисперсия (G²) является элементом расчета не только показателей вариации, но и других статистических методов анализа, прежде всего выборочного, дисперсионного и кореляционно-регрессионного.
Наиболее потребляемыми являются 2 метода упрощенного расчета дисперсии, основанные на математических свойствах дисперсии.
Первый упрощенный способ G²взвеш =х²-(х)² = Σх²f/Σf-(Σxf/Σf)²
G²прост = Σх²/n-(Σx/n)²
Расчет среднего квадрата означает исполнение условного момента второго порядка.
Упрощенный способ расчета дисперсии отсчетом от условного нуля выполняется так
G² = i²(m₂-m₁²), где i – шаг
m₁ = Σ((x-a)/i)¹*f/Σf
m₂ = Σ((x-a)/i)²*f/Σf
Можно определить три показателя колеблемости признака в сгруппированной совокупности:
общая дисперсия G²
межгрупповая (факторная) β²
средняя из групповых (остаточная) Gi²
G₀² = Σ(x -x)²f/ Σf х -х₀
β² = Σ(x -x)²fi/ Σf fi – объемы групп хi -x₀
Gi² = ΣGi² fi/Σ fi Gi²
Правило: G₀² = β² +Gi² - общая дисперсия равна сумме факторной и остаточной.
Общая дисперсия характеризует вариацию признака, зависящую от всех условий формирования совокупности. Межгрупповая (факторная) - отражает вариацию изучаемого признака, который возникает под влиянием признака фактора, положенного в основу группировки. Она характеризует колеблемость групп, т.е. частей средних, вокруг общей средней. Средняя внутригрупповая (остаточная) дисперсия – характеризует случайную вариацию в каждой отдельной группе. Эта вариация возникает под влиянием других, не учтенных в анализе факторов.
Дисперсионный анализ. Чтобы провести дисперсионный анализ по правилу сложения дисперсий сначала необходимо определить признаки совокупности, факторные и результативные признаки.
Процедура дисперсионного анализа следующая:
Определяем факторный и результативный признак.
По факторному признаку построим ряды распределения
Рассчитаем групповое среднее
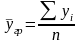
Определяем среднюю общую
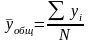
Рассчитаем групповую дисперсию
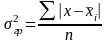
Рассчитаем среднюю из групповых дисперсий
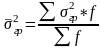
Рассчитаем межгрупповую дисперсию
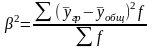
Рассчитаем общую дисперсию
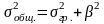
Определяем коэффициент детерминации
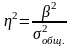
Определяем эмпирическое корреляционное отношение
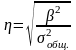
Если коэффициент эмпирического корреляционного отношения стремиться к 1, то между факторным и результативным признаками имеется прямая связь, от 80% до 100% – тесная, 60-80% – умеренная, 40-60%-слабая.
Если знак отрицательный то связь обратная.
51. Корреляция между рядами динамики
Колебания временных рядов часто бывают взаимно обусловлены. Так, например, временной ряд выпуска продукции на данном предприятии можно считать обусловленным влиянием двух факторов - стоимости производственных фондов и численности работающих, которые также изменяются во времени.
При определении коэффициентов корреляции признаков в подобных случаях необходимо помнить, что на полученные результаты оказывают влияние учитываемые в расчетах тренды временных рядов.
Изменение уровня одного ряда может вызвать изменение уровней другого через некоторый промежуток (лаг), поэтому важно оценить этот лаг и коррелировать ряды с его учетом. Оценка лага может быть произведена с помощью взаимокорреляционной функции ryx (τ), которая представляет собой ряд коэффициентов корреляции между уровнями коррелируемых рядов, сдвинутыми относительно друг друга на τ интервалов. Максимум значения определяет величину лага.
Коррелированно остатков временных рядов. Ввиду того что непосредственное коррелирование временных рядов связано с искажениями, прибегают к корреляции их остатков. Пусть тренды рядов yt и xt представлены аналитическим способом, тогда значения их остатков выразятся как:
![]()
Полученное значение коэффициента корреляции признаков, исчисленное по остаткам τ дает неискаженное представление о степени тесноты их связи:
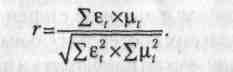
Коррелированно временных рядов с включением времени в качестве фактора. Эффект устранения влияния тренда при коррелировании временных рядов может быть достигнут включением фактора времени непосредственно в уравнение регрессии. Так, динамическая зависимость двух рядов признаков может быть представлена следующим образом:
yt=a0+ a{x1 + a2t
52. Анкета
Анкетный опрос на современном этапе один из способов получения первичной информации. Первые попытки опросов французских крестьян относятся к ХVII веку. Родоначальником анкетного опроса является ирландский ученый Дж. Гронта в 1672 году он провел социологическое исследование «Политическая анатомия Ирландии».
Анкетный опрос представляет собой метод сбора информации, основывающийся на выявлении и обобщении мнений опрашиваемых по определенной программе. Для анкетирования специально разрабатывается опросный бланк (анкета), которая содержит вопросы и фиксирует ответы.
Содержание анкетного бланка:
Преамбула (реквизиты организации, проводящей анкетный опрос);
Цель;
Основные вопросы, содержащиеся в анкете, делятся:
А) Вводные (введение)
Б) Центральные (главные)
В) Немного о себе (о респонденте)
Каждая анкета сопровождается инструкциями к заполнению и обязует о не разглашении полученной информации (т.е. гарантируется анонимность).
Технология проведения анкетного опроса может быть различна в зависимости от цели и вида. В обобщенной форме содержание и последовательность выполнения возможных этапов подготовки и проведения анкетного опроса приведено ниже (см. рис. 2. 1.)
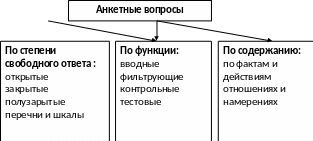
Рис. 2.1. Классификация анкетных вопросов
Этапы проведения анкетного опроса:
Определение цели и задачи опроса
Выбор метода сбора данных
Разработка вопросов
Форматирование анкеты
Предварительное тестирование
Корректировка предварительной анкеты и тиражирование её
Проведение опроса
Обработка и анализ полученных результатов
Составление отчета
По логике и фактически проведение анкетного опроса показывает, что все респонденты могут быть разделены на две группы:
Заинтересованные
Не заинтересованные.
Для заинтересованных респондентов анкета включает от 15 вопросов, а для не заинтересованных – до 10 вопросов. Однако с учетом предмета исследования, времени, средств, кадрового состава количество вопросов может изменяться.
53. Порядковые средние
Порядковые средние (структурные, позиционные) – их специфика в том, что их значения определяются величинами конкретной варианты, занимающей определенное место в ряду распределения. К числу наиболее используемых в экономическом анализе порядковых средних относятся мода и медиана.
Мода – та варианта, которая чаще других встречается в ряду распределения . Для дискретного ряда это варианта с наибольшей частотой. Мода используется, например, для определения размера ходовой обуви. Для интервальных рядов вначале отыскивается модальный интервал, а затем конкретно значение моды уже внутри интервала
Мо = Хн+h(fмо-fмо-₁)/((fмо-fмо-₁)+(fмо-fмо-₁)
Хн – нижняя граница модального интервала
h – шаг интервала
fмо – частота модального интервала
fмо-₁ - частота интервала, предшествующего модальному
fмо+₁ - частота следующего интервала за модальным
Медиана – варианта, которая делит ранжированный ряд на 2 равные по численности части. При четном количестве вариантов ряда медиана вычисляется из двух серединных.
Общее правило для дискретного ряда: для установления величины медианы определяется порядковый номер центральной варианты или двух центральных вариант. Для интервальных рядов вначале определяется интервал, где находится медиана, а затем внутри интервала рассчитывается конкретная величина медианы. Что бы найти медианный интервал надо рассчитать ряд кумулятивных частот и по накоплению найти интервал, где находится серединная варианта. Расчетная формула:
Ме = Хн+h((0,5f-Sме-₁)/fме)
f – Объем ряда
Sме-₁ - частота, накопленная до начала медианного интервала
Fме – частота медианного интервала
54. Корреляция между рядами динамики
Колебания временных рядов часто бывают взаимно обусловлены. Так, например, временной ряд выпуска продукции на данном предприятии можно считать обусловленным влиянием двух факторов - стоимости производственных фондов и численности работающих, которые также изменяются во времени.
При определении коэффициентов корреляции признаков в подобных случаях необходимо помнить, что на полученные результаты оказывают влияние учитываемые в расчетах тренды временных рядов.
Изменение уровня одного ряда может вызвать изменение уровней другого через некоторый промежуток (лаг), поэтому важно оценить этот лаг и коррелировать ряды с его учетом. Оценка лага может быть произведена с помощью взаимокорреляционной функции ryx (τ), которая представляет собой ряд коэффициентов корреляции между уровнями коррелируемых рядов, сдвинутыми относительно друг друга на τ интервалов. Максимум значения определяет величину лага.
Коррелированно остатков временных рядов. Ввиду того что непосредственное коррелирование временных рядов связано с искажениями, прибегают к корреляции их остатков. Пусть тренды рядов yt и xt представлены аналитическим способом, тогда значения их остатков выразятся как:
Полученное значение коэффициента корреляции признаков, исчисленное по остаткам τ дает неискаженное представление о степени тесноты их связи:
Коррелированно временных рядов с включением времени в качестве фактора. Эффект устранения влияния тренда при коррелировании временных рядов может быть достигнут включением фактора времени непосредственно в уравнение регрессии. Так, динамическая зависимость двух рядов признаков может быть представлена следующим образом:
yt=a0+ a{x1 + a2t
