Шпоры СГ11

32. Метод многомерного поиска первого порядка – наискорейшего спуска

На каждой итерации задача одномерной оптимизации решается точно.

При использовании метода наискорейшего спуска на каждой итерации величина шага λ^k выбирается из условия минимума функции f(x) в направлении спуска.

31. Прямой метод Хука-Дживса для решения задач многомерного поиска

Метод нелинейной оптимизации нулевого порядка – не использующий значения производных функций, применяется в том случае, если значения производных сложно получить в виде аналитических функций или процесс вычисления производных довольно трудоемкий.

Метод Хука-Дживса для поиска безусловного локального экстремума функции. Алгоритм делится на две фазы: исследующий поиск и поиск по направлению.

30. Прямой метод Гаусса для решения задач многомерного поиска

29. Одномерный поиск на унимодальных функциях: метод Фибоначчи

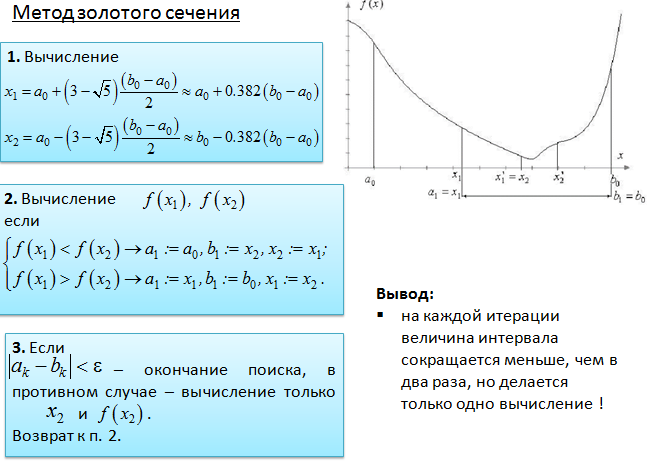
28. Одномерный поиск на унимодальных функциях: метод золотого сечения

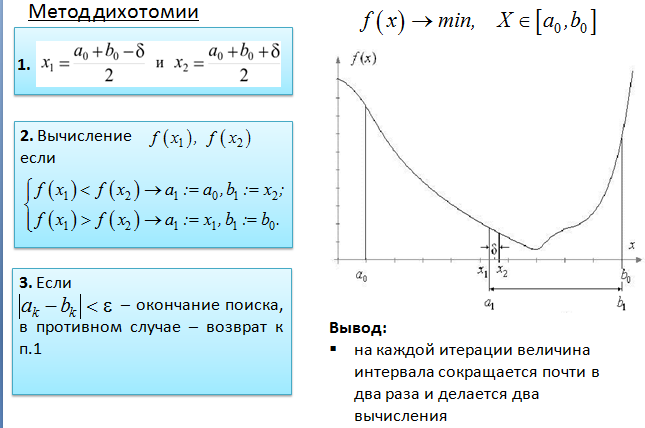
27. Одномерный поиск на унимодальных функциях: метод дихотомии

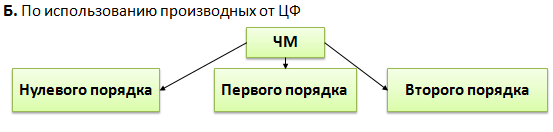
26. Классификация численных методов решения задач нелинейного программирования

Численные методы – в которых решение задачи НП ищется эвристическим подбором значений неизвестных, доставляющих экстремум min или max целевой функции.

( набор расчетных точек фиксировано (значение очередной расчетной точки

и определено априорно) определяется по рез-ту предыд. итерации)

Пассивный (выбор стартовой точки) => переход к последовательному.

d² f / d x² < 0 – первого порядка

d² f / d x² > 0 – второго порядка

Численные методы многомерных задач сводится к комбинации одномерных.

25. Метод неопределенных множителей Лагранжа для решения задач нелинейного программирования

24. Определение и свойства унимодальных и многомодальных функций

Унимодальная функция – на интервале от а до b, если внутри этого интервала существует точка, слева от которой функция только возрастает, справа – убывает.

Основное свойство унимодальных функций, используемое при поиске точек минимума, состоит в том, что вычисление любых двух значений f(x₁), f(x₂), x₁ ¹ x₂, x₁,x₂ Î [a,b] позволяет уменьшить интервал поиска точки минимума. Для решения задачи одномерной оптимизации с унимодальной целевой функцией применяется метод золотого сечения и метод чисел Фибоначчи.

Многомодальная функция – содержит внутри интервала [a, b] несколько точек аналогичных свойству унимодальной.

Задачи нелинейного программирования решаются так: дифференциал означает, что функция определена в сколь угодно малой окрестности возле точки вычисления производно.

grad [f(x)] = 0 – вектор, указывающий направление возрастающей функции.

Правила НП:

1. На области допустимых значений находятся все точки (grad = 0 или производная = 0).

2. С помощью специальных методов находятся все значения целевой функции на границах допустимых значений.

3. Простым переборным сравнением среди стац. и граничных точек, выбирается точка, соотв. наибольшим или наименьшим значением целевой функции.

23. Методы решения задачи нелинейного программирования на примере задачи максимизация площади прямоугольника ,вписанного в окружность.

Найти стороны прямоугольника максимальной площади, вписанного в окружность радиуса R.

В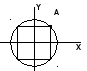озьмем на окружности точку А(х, у), тогда математическое описание задачи примет следующий вид:

S = 4xy  max;

x² + y² – R² = 0;

x, y  0.

1. Составим функцию Лагранжа: L = f + g = 4xy +  (x² + y² – R²).

2.

Решим систему уравнений.

3. Из первого уравнения: .

Подставляем во второе уравнение: 4x – ²x = 0; x(4 – ²)= 0;

x = 0, ₁ =2, ₂ = –2.

Корень х =0 не удовлетворяет условиям задачи. По аналогичной причине отбрасываем корень ₁:

₁ = 2: y = – x/2 = – 2х/2 = –x  0.

₂ = –2: y = – x/2 = x.

4. Оставляем корень ₁ = 2.

Подставив в третье уравнение системы, получаем .

22. Общая формулировка задачи нелинейного программирования.

21. Решение задач динамического программирования методом направленного перебора.

20. Методы решения задач динамического программирования.

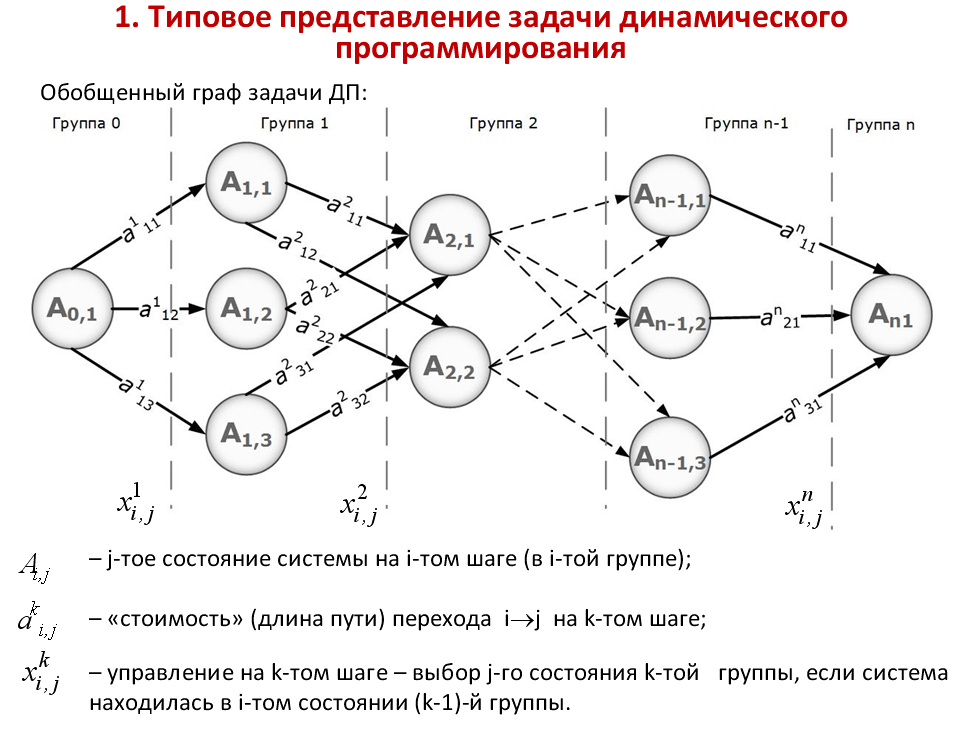
19. Типовое представление и формулировка задачи динамического программирования.

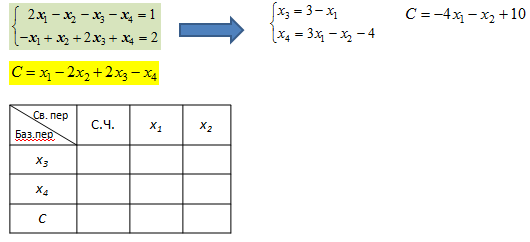
18. Табличный алгоритм симплекс-метода решения задач линейного программирования.

Этапы:

1. Формулировка ОЗЛП.

2. Выбор (n-m) свободных переменных и выражение базисных переменных через свободные.

3. Заполнение стартовой таблицы: внесение коэффициентов при переменных с противоположным знаком.

4. Выбирается разрешающий столбец и строка, разрешающий элемент.

5. Переменные, соответствующие разрешающей строке и столбцу меняются местами по определенному правилу осуществляется модификация таблицы:

- обмен между свободными и базисными переменными.

- разрешающий элемент заменяется на обратный.

- элементы разр.строки делятся на разрешающий элемент.

- элементы разр.столбца делятся на разрешающий элемент и меняют знак.

- ко всем остальным элементам из старой таблицы прибавляется произведение элемента разрешающей строки старой таблицы, расположенного в том же столбце на элемент разрешающего столбца новой таблицы, расположенного в той же строке. Пока не достигнем оптимального решения.

17. Геометрическая интерпретация решения задач линейного программирования.