6. Примеры решения задач

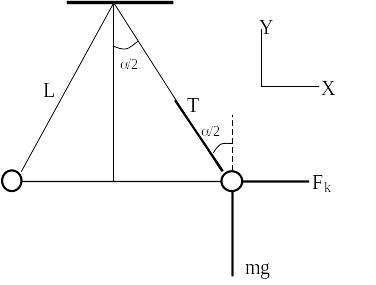
1. Два шарика одинакового объема, обладающие массой 0,6·10^-3 г каждый, подвешены на шёлковых нитях длиной

0,4 м так, что их поверхности соприкасаются. Угол, на который разошлись нити при сообщении шарикам одинаковых зарядов, равен 60⁰. Найти заряд и силу электрического отталкивания.

Дано: m = 0,6·10^-3 г = 0,6·10^-7 кг; L= 0,4 м; α = 60⁰; q₁ = q₂ = q.

Найти: q, F.

Решение: В результате электростатического отталкивания заряды разойдутся на расстояние равное 0,4 м. Используя

условие равновесия, запиш

ем: .

Найдём проекции сил на оси Х и Y. На ось Х:

. (1);

на ось Y:

(2).

Поделим уравнение (1) на уравнение (2), получаем: . Учитывая что , где k = 9·10⁹ Н·м²/Кл² , получим:

, откуда: .

Сделаем подстановку числовых данных:

= 7,8·10^-9 Кл.

При этом сила отталкивания шариков будет равна:

.

Ответ: F_k = 3,4·10^-6 Н, q = 7,8·10^-9 Кл.

2. Вычислить ускорение, c которым разлетаются два электрона, находящиеся в вакууме на расстоянии 1 мм друг от друга.

Дано: q = 1.6·10^-19 Кл; r = 1 мм = 10^-3 м.

Найти: а.

Решение. По закону Кулона электроны, находящиеся на расстоянии r, взаимодействуют (отталкиваются) с силой:

, (1)

Под действием этой силы в соответствии со вторым законом Ньютона электрон приобретает ускорение: , (2), где m – масса электрона.

Тогда с учетом (1) и (2) ускорение равно: ;

Подставим числовые значения:

≈ 2,5· 10⁸ (м/с² ).

Ответ: а = 2,5·10⁸ м/с².

3. Электрическое поле создано длинным цилиндром радиусом 1 см, равномерно заряженным с линейной плотностью 20 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстоянии 0,5 см и 2 см от поверхности цилиндра в средней его части.

Дано: R = 1 cм = 10^-2 м; τ = 20·10^-9 Кл/м; а₁= 0,5 см = 5·10^-3 м;

а₂ = 2·10^-2 м.

Найти: φ₁ - φ₂

Решение. Для определения разности потенциалов воспользуемся соотношением между напряженностью поля и градиентом потенциала: . (1)

Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде:

, или d = - Edr. (2)

Интегрируя это выражение, найдем разность потенциалов двух точек, отстоящих на расстояниях r₁ и r₂ от оси цилиндра:

. (3)

Так как цилиндр длинный и точки взяты вблизи его средней части, то для выражения напряженности поля можно воспользоваться формулой напряженности поля, создаваемого бесконечно длинным цилиндром: .

Подставив это выражение для Е в (3), получим:

Или (4)

Выразим τ и в единицах системы СИ:

τ = 20 нКл/м = 2·10^-8 Кл/м; м/Ф.

Так как величины r₁ и r₂ входят в формулу (4) в виде отношения, то их можно выразить в любых, но только одинаковых единицах: см; см.

Подставим числовые значения в (4):

= 250 В.

Ответ: 250 В.

4. Определить ускоряющую разность потенциалов, которую должен пройти в электрическом поле электрон, обладающий скоростью 10⁶ м/с, чтобы его скорость возросла в 2 раза.

Дано: v₁ = 10⁶ м/с; v₂/v₁ = n = 2.

Найти: ₂ - ₁ = U.

Решение. Ускоряющую разность потенциалов можно найти, вычислив работу А сил электростатического поля по

перемещению электрона. Эта работа определяется произведением заряда электрона на разность потенциалов: А = eU. (1)

Работа сил электростатического поля в данном случае равна изменению кинетической энергии электрона:

(2)

где T₁ и T₂- кинетические энергии электрона до и после

ускорения, m – масса, v₁ и v₂ - начальная и конечная скорости электрона. Приравняв правые части равенств (1) и (2),

получим: или: ,

где Отсюда искомая разность потенциалов:

(3)

Подставим числовые значения физических величин и выполним вычисления:

Ответ: U = 8,53 В.

5. Конденсатор емкостью 3 мкФ был заряжен до разности потенциалов 40 В. После отключения от источника тока конденсатор был соединен параллельно с другим незаряженным конденсатором емкостью 5 мкФ. Какая энергия

израсходуется на образование искры в момент присоединения второго конденсатора к первому?

Дано: С₁ = 3 мкФ; С₂ = 5мкФ; U₁ = 40 В

Найти: W'

Решение. Энергия W', израсходованная на образование искры:

, (1)

где W₁- энергия, которой обладал первый конденсатор до присоединения к нему второго конденсатора; W₂ - энергия, которую имеет батарея, составленная из первого и второго конденсаторов. Энергия заряженного конденсатора определяется по формуле: , (2)

где С - электроёмкость, а U- разность потенциалов на обкладках конденсатора.

Подставив в формулу (1) выражения для энергий W₁ и W₂ в соответствии с формулой (2) и принимая во внимание, что общая емкость параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов, получим:

(3)

где С₁ и С₂- емкости первого и второго конденсаторов; U₁ - разность потенциалов, до которой был заряжен первый конденсатор; U₂ - разность потенциалов на зажимах батареи конденсаторов.

Учитывая, что заряд после присоединения второго конденсатора остался прежний, выразим разность потенциалов U₂ следующим образом:

Подставив выражение для U₂ в формулу (3), получим:

После простых преобразований найдем:

Подставляем числовые значения:

= 1,5 мДж.

Ответ: W' = 1,5 мДж.

6. Сила тока в проводнике сопротивлением 20 Ом нарастает в течение времени 2 сек. по линейному закону от I₀ = 0 до I = 6 А. Определить теплоту, выделившуюся в этом проводнике Q₁ за первую и Q₂ за вторую секунды, а также найти их отношение.

Дано: R = 20 Ом; Δt = 2 с; I = 6 А.

Найти: Q₁; Q₂;

Решение. Запишем закон Джоуля-Ленца в виде: dQ =I²Rdt (1).

Здесь сила тока I является некоторой функцией времени, а именно: I = kt, (2), где k – коэффициент пропорциональности, численно равный приращению силы тока в единицу времени, т.е: А/с.

С учетом (2) формула (1) примет вид: (3)

Для определения теплоты, выделившейся за промежуток времени , выражение (3) надо проинтегрировать в пределах

от t₁ до t₂:

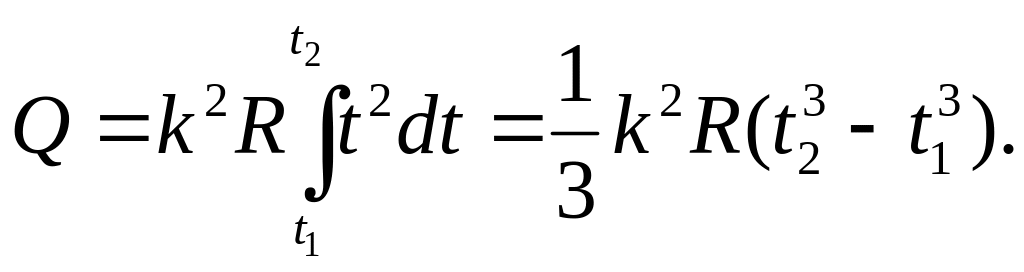
При определении теплоты, выделившейся за первую секунду,

пределы интегрирования равны t₁ = 0, t₂ = 1 c. Следовательно:

Дж.

За вторую секунду t₂ = 2 c, t₁ = 1 c:

= 420 Дж.

Отсюда:

т.е. за вторую секунду выделится теплоты в 7 раз больше, чем за первую.

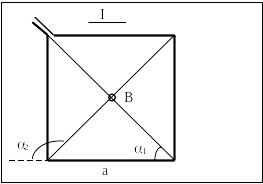
7. По проводу, согнутому в виде квадрата со стороной

10 см, течет ток силой 100 A. Найти магнитную индукцию В

в точке пересечения диагоналей квадрата.

Дано: I = 100 А; а = 10 см = 0,1 м.

Найти: В

Р

ешение: Расположим квадратный виток в плоскости чертежа (см. рисунок). Согласно принципу суперпозиции индукция магнитного поля В в центре квадратного витка будет равна векторной сумме индукций магнитных полей, создаваемых каждой стороной квадрата в отдельности:

(1)

В точке пересечения диагоналей квадрата все векторы индукции магнитного поля от каждой из сторон рамки будут расположены перпендикулярно плоскости витка и направлены ‹‹от нас››. Кроме того, из соображений симметрии следует, что абсолютные значения этих векторов одинаковы по величине и направлению: В₁= В₂= В₃= В₄. Это позволяет векторное равенство (1) заменить скалярным: В = 4В₁. (2)

Магнитная индукция В₁ поля, создаваемого отрезком прямолинейного провода с током, выражается формулой:

(3)

Учитывая, что и (см. рис.),

формулу (3) можно переписать в виде:

Подставив это выражение для В₁ в формулу (2), находим:

Заметив, что , а ( ), получим:

Подставив числовые значения физических величин, проведем вычисления: мТл

Ответ: В = 1,13 мТл

8. Плоский квадратный контур со стороной 10 см, по которому течет ток 100 A, свободно установился в однородном магнитном поле с индукцией 1 Тл. Определить работу, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1) φ₁ = 90⁰; 2) φ₂ = 3⁰. При повороте контура сила тока в нем поддерживается постоянной.

Дано: а = 10 см; I = 100 A; В = 1 Тл; ₁ = 90⁰; ₂ = 3⁰.

Найти: А₁, А₂.

Решение. Как известно, на контур с током, помещенном в магнитное поле, действует момент сил: , (1)

где р_m- магнитный момент контура; φ - угол между магнитным моментом р_m, вектор которого направлен по нормали к плоскости контура, и направлением индукции магнитного поля В.

По условию задачи, в начальном положении контур свободно установился в магнитном поле. При этом момент сил, действующих на контур с током, равен нулю (М = 0), а значит, φ = 0, т.е. вектора и совпадают по направлению.

Если внешние силы выведут контур из положения равновесия, то возникший момент сил, определяемый формулой (1), будет стремиться возвратить контур в исходное положение.

Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменный (зависит от угла поворота φ), то для расчета работы применим формулу в дифференциальной форме: .

Подставив в эту формулу выражение М по (1) и, учитывая, что p_m = IS = Ia², где I – сила тока в контуре; S = a² – площадь контура, получим: .

Взяв интеграл от этого выражения, найдем работу при повороте рамки на конечный угол :

. (2)

1) Найдем работу при повороте рамки на угол φ₁ = 90⁰:

. (3)

Выразим числовые значения величин в единицах СИ:

I = 100 A; В = 1 Тл; а = 10 см = 0,1 м и подставим в (3):

= 1 Дж.

2) Вычислим работу при повороте рамки на угол φ₂ = 3⁰. Учитывая, что угол φ₂ мал, а для малых углов sin φ ≈ φ, выражение (2) принимает вид:

(4)

Выразим угол φ₂ в радианах. После подстановки в (4)

числовых значений величин находим:

= 1,37·10^-3 Дж = 1,37 мДж.

Отметим, что задача могла быть решена и другим способом. Известно, что работа внешних сил по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока через контур:

,

где Ф₁ – магнитный поток, пронизывающий контур до перемещения; Ф₂ – то же, но после перемещения контура.

В случае φ₁ = 90⁰ поток Ф₁ = BS, а Ф₂ = 0. Следовательно,

,

что совпадает с полученным выше результатом (3).

9. Электрон, пройдя ускоряющую разность потенциалов 400 В, попал в однородное магнитное поле напряженностью 10³ А/м. Определить радиус кривизны траектории и частоту обращения электрона в магнитном поле. Вектор скорости электрона перпендикулярен линиям напряженности магнитного поля.

Дано: U = 400 В; H = 10³ А/м;

Найти: R; f.

Решение. Радиус кривизны траектории электрона определим, исходя из следующих соображений: на движущийся в магнитном поле электрон действует сила Лоренца (действием силы тяжести можно пренебречь). Сила Лоренца перпендикулярна вектору скорости и, следовательно, сообщает электрону нормальное ускорение:

, или , (1)

где е – заряд, v- скорость, m - масса электрона; В - индукция магнитного поля; R - радиус кривизны траектории электрона; - угол между направлением вектора скорости и вектором (в данном случае , следовательно ).

Из формулы (1) находим: (2)

Входящий в равенство (2) импульс mv может быть выражен через кинетическую энергию электрона: (3)

Но кинетическая энергия Т электрона, прошедшего ускоряющую разность потенциалов U, определяется равенством:

Подставив это выражение в формулу (3), получим:

Магнитная индукция В связана с напряженность H магнитного поля в вакууме соотношением , где - магнитная постоянная. Подставив найденные выражения для В и mv в формулу (2), определим: (4)

Выразим все величины, входящие в формулу (4), в единицах системы СИ: m = 9.11∙10^-31 кг; е = 1,60∙10^-19 Кл; U = 400 B, Гн/м; H = 10³ А/м. Подставим эти значения в формулу (4) и произведем вычисления:

= 5,37∙10^-2 м= 5,37 см.

Для определения частоты обращения f воспользуемся формулой, связывающей частоту со скоростью и радиусом траектории электрона:

(5)

Подставив выражение (2) в формулу (5), получим для радиуса кривизны электрона:

, или .

Подставим все величины, входящие в эту формулу, в единицах системы СИ и произведем вычисления:

Ответ: R = 5,37 см; f = 3,5210⁷ с^-1

10. Резонанс в колебательном контуре, содержащем конденсатор С₁ емкостью 1 мкФ, наступает при частоте 400 Гц. Когда параллельно конденсатору С₁ подключили еще один конденсатор емкостью С₂, резонансная частота становится равной 100 Гц. Найти емкость конденсатора С₂.

Дано: С₁ = 1 мкФ; f₁ = 400 Гц; f₂ = 100 Гц.

Найти: С₂

Решение. Резонанс в приемном колебательном контуре наступает при условии, когда собственная частота колебаний контура становится равной частоте вынужденных колебаний, возбуждаемых внешним передатчиком. При этом амплитуда электромагнитных колебаний в контуре становится

максимальной. Частота вынужденных колебаний, равная собственной частоте колебательного контура, называется резонансной частотой.

Резонансная частота ν₁ в колебательном контуре, содержащем только один конденсатор С₁, определяется формулой Томсона: (1)

где L – индуктивность катушки в колебательном контуре.

Когда к конденсатору С₁ подключили параллельно второй конденсатор С₂, емкость образованной батареи конденсаторов стала равна С₁+С₂, и при этом резонансная частота f₂ стала равной: (2)

Обе частоты f₁ и f₂, а также емкость С₁ известны. Неизвестна индуктивность катушки L и искомая емкость С₂. Если исключить из этих двух уравнений индуктивность L, то получим одно уравнение с одним неизвестным - ёмкостью С₂. Для этого необходимо поделить левые и правые части уравнений (1) и (2) соответственно. Выполним эти действия:

, .

Отсюда: 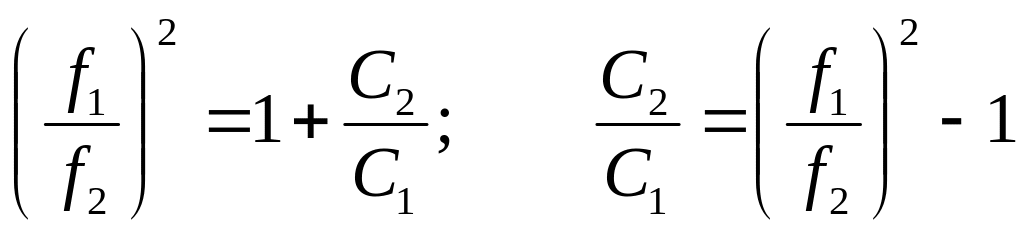, и, наконец:

. Задача решена в общем виде.

Переведем заданные величины в систему СИ: 1 мкФ = 10^-6 Ф.

Подставим численные значения в полученную формулу и произведем вычисления:

= 1,5·10^-5 Ф.

Ответ: С₂ = 1,5·10^-5 Ф.