Проверка гипотезы о значении дисперсии генеральной совокупности

В качестве критерия проверки нулевой гипотезы Н₀: σ²= σ₀² принимают случайную величину , (3.11)

которая имеет распределение с ν=n-1 степенями свободы.

Правило 1. Если Н₁: , то строят двустороннюю критическую область. Левую ( ) и правую ( ) границы критической области находят из условий:

Р(χ²> (1- ; ν))=1- , (3.12)

Р(χ²> (1- ; ν))= .

В этом случае правило проверки гипотезы сводится к следующему: если , то у нас нет основания отвергнуть гипотезу. Если же < или > , то гипотезу отвергают.

Правило 2. Если Н₁: , то строят правостороннюю критическую область и находят из условия: Р(χ²> (α; ν))= α. (3.13)

Если > , то нулевую гипотезу отвергают, если же < , то нулевая гипотеза не противоречит опытным данным.

Правило 3. Если Н₁: , то строят левостороннюю критическую область и находят из условия: Р(χ²> (1-α; ν))= 1-α. (3.14)

Если < , то нулевую гипотезу отвергают, если же , то нулевая гипотеза не отвергается.

Сравнение наблюдаемой относительной частоты с гипотетической вероятностью появления события

Пусть по достаточно большому числу n независимых испытаний, в каждом из которых вероятность р появления события А постоянна, но неизвестна, найдена относительная частота . Требуется при заданном уровне значимости α проверить нулевую гипотезу Н₀: р= р_0.

Для проверки нулевой гипотезы используется статистика

t_н = , (3.15)

при больших n (n>0), имеющей приближенно нормальное распределение.

Правило 1. При конкурирующей гипотезе Н₁: р р₀ критическую точку t_кр двусторонней критической области находят из условия: Ф(t_кр)= 1- α. (3.16)

Если < t_кр – нет оснований отвергнуть нулевую гипотезу, если > t_кр - нулевую гипотезу отвергают.

Правило 2. При конкурирующей гипотезе Н₁: р>р₀ критическую точку t_кр правосторонней критической области находят из условия: Ф(t_кр)= 1- 2α. (3.17)

Если t_н < t_кр – нет оснований отвергнуть нулевую гипотезу, если t_н > t_кр  - нулевую гипотезу отвергают.

Правило 3. При конкурирующей гипотезе Н₁: р<р₀ находят критическую точку t_кр по правилу 2, затем полагают границу левосторонней критической области = - t_кр . Если t_н >- t_кр – нет оснований отвергнуть нулевую гипотезу, если t_н <- t_кр - нулевую гипотезу отвергают.

При использовании вышеприведенных правил следует иметь ввиду, что удовлетворительные результаты обеспечивает выполнение неравенства np₀q₀ >9.

Сравнение двух средних нормальных генеральных совокупностей

Дисперсии генеральных совокупностей известны. Пусть X и Y - нормальные генеральные совокупности с известными дисперсиями и и неизвестными математическими ожиданиями μ_х и μ_у.

Из генеральных совокупностей взяты две независимые выборки объемом n_х и n_у. Пусть - средние арифметические выборочных совокупностей. Требуется проверить нулевую гипотезу Н₀: μ_х= μ_у на уровне значимости α.

Для проверки нулевой гипотезы используется следующая статистика:

t_н = 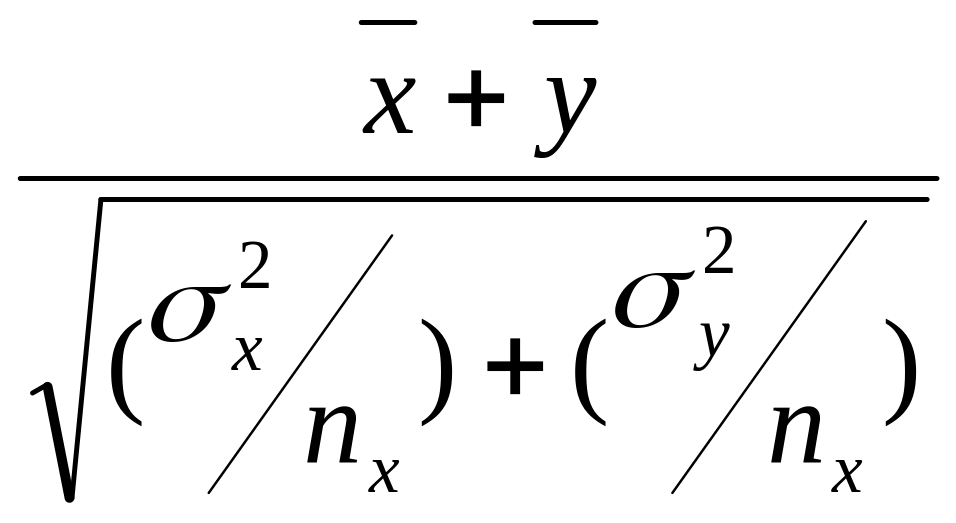, (3.17)

имеющая нормальное нормированное распределение с параметрами N(0;1)

Правило 1. При конкурирующей гипотезе Н₁: μ_х μ_у критическую точку t_кр двусторонней критической области находят из условия: Ф(t_кр)=1- α. (3.18)

Если < t_кр – нет оснований отвергнуть нулевую гипотезу, если > t_кр - нулевую гипотезу отвергают.

Правило 2. При конкурирующей гипотезе Н₁: μ_х > μ_у критическую точку t_кр правосторонней критической области находят из условия: Ф(t_кр)=1- 2α. (3.19)

Если t_н < t_кр – нет оснований отвергнуть нулевую гипотезу, если t_н > t_кр  - нулевую гипотезу отвергают.

Правило 3. При конкурирующей гипотезе Н₁: μ_х < μ_у находят критическую точку t_кр по правилу 2, затем полагают границу левосторонней критической области = - t_кр . Если t_н >- t_кр – нет оснований отвергнуть нулевую гипотезу, если t_н <- t_кр - нулевую гипотезу отвергают.

Дисперсии генеральных совокупностей неизвестны. Для проверки нулевой гипотезы Н₀: μ_х= μ_у на уровне значимости α используют статистику:

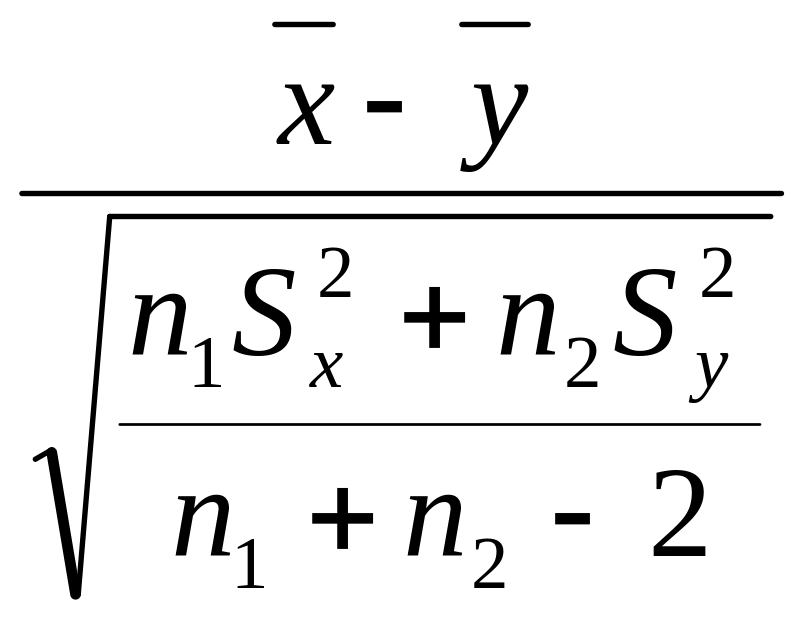
t_н = , (3.20)

имеющую распределение Стьюдента с числом степеней свободы ν= n_х+ n_у –2.

Правило 1. При конкурирующей гипотезе Н₁: μ_х μ_у критическую точку t_кр(α;ν) двусторонней критической области находят из условия:

St(t_кр; ν)=Р( >t_кр)= α (3.21)

Если < t_кр(α; ν) – нет оснований отвергнуть нулевую гипотезу. Если > t_кр(α; ν) – нулевую гипотезу отвергают.

Правило 2. При конкурирующей гипотезе Н₁: μ_х > μ_у критическую точку правосторонней области находят из равенства St(t_кр; ν)=Р( >t_кр)= 2α. (3.22)

Если t_н < t_кр(2α; ν) – нет оснований отвергнуть нулевую гипотезу. Если t_н > t_кр(2α; ν) – нулевую гипотезу отвергают.

Правило 3. При конкурирующей гипотезе Н₁: μ_х < μ_у сначала находят вспомогательную критическую точку t_кр по правилу 2, а затем полагают границу левосторонней критической области = - t_кр. Если t_н > -t_кр(2α; ν) - нет оснований отвергнуть нулевую гипотезу, если t_н< -t_кр(2α; ν) – нулевую гипотезу отвергают.

Проверка гипотезы о равенстве генеральных дисперсий двух нормальных совокупностей

Пусть X и Y генеральные совокупности, значения признаков которых распределены по нормальному закону с дисперсиями и . Из этих совокупностей взяты независимые случайные выборки объемом n_х и n_у , и пусть и , причем > . Требуется на заданном уровне значимости α проверить нулевую гипотезу Н₀: = . Для проверки нулевой гипотезы используется статистика

F_н = , (3.23)

подчиняющаяся распределению Фишера-Снедекора (F-распределение) с ν₁=n_х–1 и ν₂= n_у –1.

Правило 1. При конкурирующей гипотезе Н₁: критическую точку F_кр двусторонней критической области находят из условия:

P (F> F_кр(α/2; ν₁; ν₂))= α/2. (3.24)

Если F_н < F_кр - нет оснований отвергнуть нулевую гипотезу, если F_н > F_кр - нулевую гипотезу отвергают.

Правило 2. При конкурирующей гипотезе Н₁: > критическую точку F_кр двусторонней критической области находят из условия:

P (F> F_кр(α; ν₁; ν₂))= α. (3.25)

Если F_н < F_кр - нет оснований отвергнуть нулевую гипотезу, если F_н > F_кр - нулевую гипотезу отвергают.

Проверка гипотезы об однородности ряда дисперсий.

При сравнении более двух генеральных дисперсий применяют два наиболее часто употребляемых критерия: критерий Бартлета и критерий Кохрана.

Критерий Бартлета. Пусть генеральные совокупности Х_1, Х₂,…,Х_l распределены нормально. Из этих совокупностей извлечены независимые выборки различных объемов n_{i .} По выборкам найдены исправленные дисперсии , ,…, . Требуется на уровне значимости α проверить нулевую гипотезу:

Н₀: = =….= .

В качестве выборочной характеристики используется статистика, предложенная Бартлетом: = 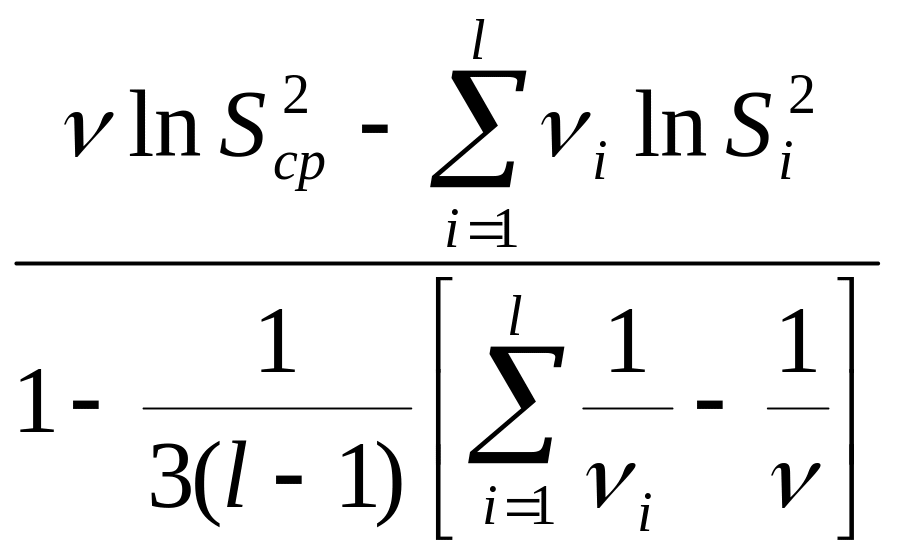, (3.26)

При >3 величина приближенно имеет распределение с ν= l-1 степенями свободы, где l - число выборок; -исправленная выборочная дисперсия i – ой выборки; = 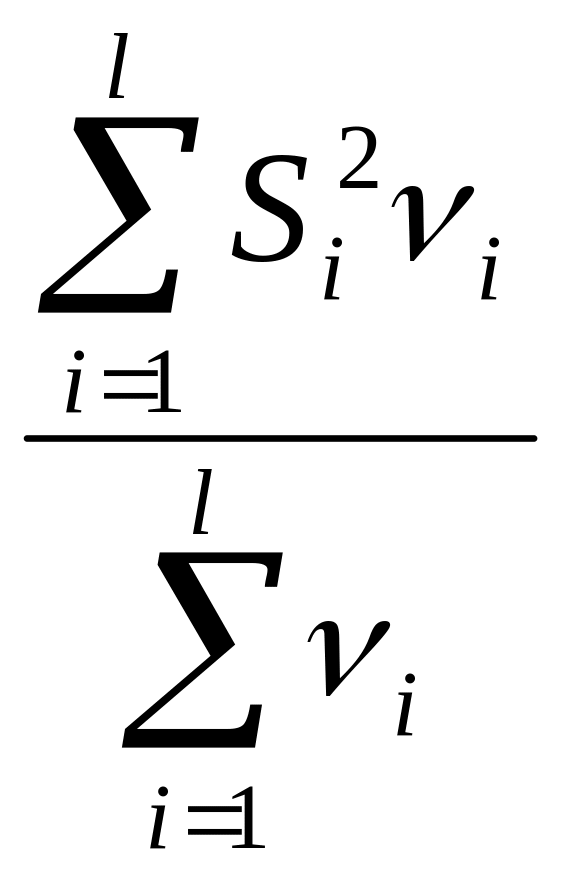- среднее значение исправленной дисперсии по всем l выборкам.

Правило. Для проверки нулевой гипотезы строят правостороннюю критическую область, границы которой находят по таблице распределения из условия: P ( > (α; ν=l-1)= α. (3.27)

Если < - нет оснований отвергнуть нулевую гипотезу, если > - нулевую гипотезу отвергают.

Критерий Кохрана. Данный критерий применяется для проверки на уровне значимости α нулевой гипотезы Н₀: = =….= по выборкам разных объемов n_i. В качестве выборочной характеристики используется статистика, предложенная Кохраном: G= , (3.28)

имеющая G – распределение с числом степеней свободы ν₁= n –1 и ν₂= l, где l – число сравниваемых совокупностей.

Для проверки нулевой гипотезы строят правостороннюю критическую область, границу которой G_кр определяют по таблице G – распределения, исходя из условия: P (G_н > G_кр (α; ν))= α. (3.29)

Если G_н < G_кр - то нулевая гипотеза не отвергается.