Контрольные вопросы и задачи

4.1. На основании выборочных данных о производительности труда (Y) и средней загрузки мощностей (Х), полученных с однотипных предприятий (табл.1) а) найдите точечную оценку коэффициента корреляции между Х и Y; б) на уровне значимости =0.05 проверьте значимость коэффициента корреляции и в) найдите его интервальную оценку при =0.95.

Х	30	35	26	34	24	41	32	36	40	37
Y	47	60	45	55	40	49	51	55	55	59

4.2. На основании полученной выборки n=30 для трех показателей Х, Y и Z рассчитаны парные коэффициенты корреляции: =0.91, =0.65 =0.74. Рассчитайте частные коэффициенты корреляции, проверьте их значимость ( =0.05) и постройте для значимых коэффициентов доверительные интервалы ( =0.95).

4.3. По данным задачи 4.2 рассчитайте множественные коэффициенты корреляции, множественные коэффициенты детерминации и проверьте их значимость.

4.4. Знания десяти студентов проверены по двум тестам: А и В. Оценки по стобалльной системе приведены в таблице 2.

А	98	94	88	80	76	70	63	61	60	58
В	99	91	93	74	78	65	64	66	52	53

Найдите выборочный коэффициент ранговой корреляции Спирмена между оценками по двум тестам и проверьте его значимость.

4.5. По данным задачи 4.1 постройте уравнение регрессии зависимости производительности труда (Y) от средней загрузки мощностей (Х), проверьте значимость уравнения, постройте интервальную оценку для коэффициента регрессии .

4.6. Дано уравнение регрессии и несмещенные оценки дисперсии коэффициентов регрессии и : =0.0028 и =2.24. На уровне значимости =0.05 проверьте значимость коэффициентов регрессии и , если n=10.

4.7. Исследуется зависимость между средней урожайностью Х (ц/га) и средней себестоимостью 1 ц (Y). Известно, что =30 ц/га , = 16 ц, =10.1, =4.24, =0.21. Рассчитайте коэффициент эластичности и коэффициент .

Тема 5. Многомерные статистические методы

Многомерный статистический анализ – раздел математической статистики, посвященный математическим методам построения оптимальных планов сбора, систематизации и обработки многомерных статистических данных, направленным на выявление характера и структуры взаимосвязей между компонентами исследуемого многомерного признака и предназначенным для получения научных и практических выводов. Под многомерным признаком понимается р-мерный вектор признаков , среди которых могут быть количественные, порядковые и классификационные. Результаты измерения этих показателей на каждом из n объектов исследуемой совокупности образуют последовательность многомерных наблюдений, или исходный массив многомерных данных для проведения многомерного статистического анализа. В рамках многомерного статистического анализа многомерный признак х интерпретируется как многомерная случайная величина, и соответственно, последовательность многомерных наблюдений как выборка из генеральной совокупности.

К основным методам многомерного статистического анализа можно отнести кластерный анализ, дискриминантный анализ, компонентный анализ, факторный анализ и метод канонических корреляций. Данные методы имеют достаточно сложный математический аппарат и обычно являются частью статистических пакетов прикладных программ.

Кластерный анализ – это совокупность методов классификации многомерных наблюдений или объектов, основанных на определении понятия расстояния между объектами с последующим выделением из них групп, «сгустков» наблюдений (кластеров, таксонов). При этом не требуется априорной информации о распределении генеральной совокупности. Выбор конкретного метода кластерного анализа зависит от цели классификации. Кластерный анализ используется при исследовании структуры совокупностей социально-экономических показателей или объектов: предприятий, регионов, социологических анкет и т.д.

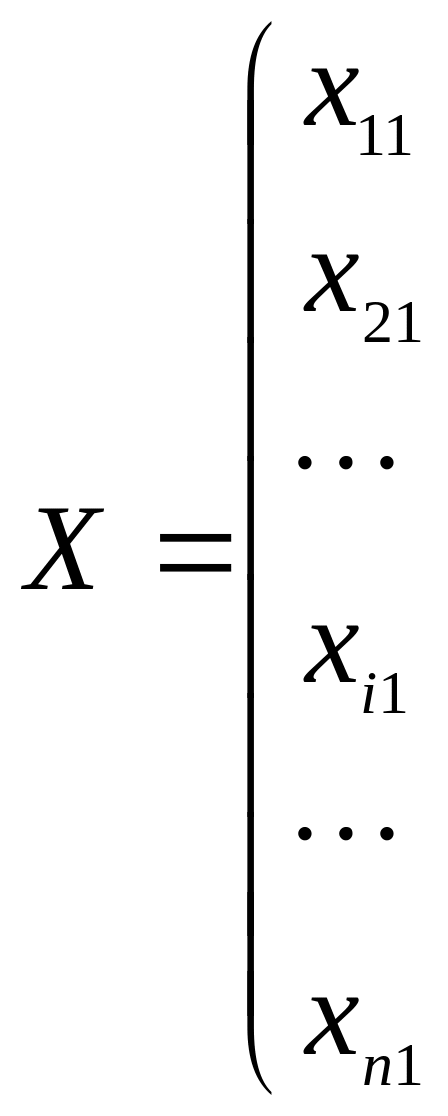
От матрицы исходных данных (5.1)

переходим к матрице нормированных значений Z c элементами , (5.2)

где j =1,2,…,k – номер показателя, i=1,2,…,n – номер наблюдения;

= = . (5.3)

В качестве расстояния между двумя наблюдениями и используют «взвешенное» евклидово расстояние, определяемое по формуле:

, где -«вес» показателя; .

Если =1 для всех l=1,2,.k, то получаем обычное евклидово расстояние:

(5.4)

Полученные значения удобно представить в виде матрицы расстояний

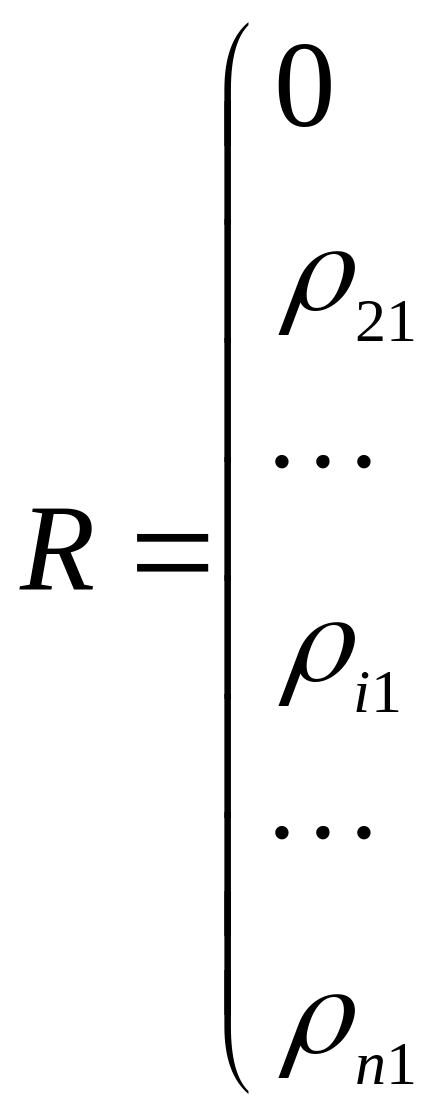
(5.5)

Так как матрица R симметрическая, т.е. , то достаточно ограничиться записью наддиагональных элементов матрицы.

Используя матрицу расстояний, можно реализовать агломеративную иерархическую процедуру кластерного анализа. Расстояния между кластерами определяют по принципу «ближайшего соседа» или «дальнего соседа». В первом случае за расстояние между кластерами принимают расстояние между ближайшими элементами этих кластеров, а во втором- между наиболее удаленными друг от друга.

Принцип работы иерархических агломеративных процедур состоит в последовательном объединении групп элементов сначала самых близких, а затем все более отдаленных друг от друга. На первом шаге алгоритма каждое наблюдение , , рассматривается как отдельный кластер. В дальнейшем на каждом шаге работы алгоритма происходит объединение двух самых близких кластеров, и вновь строится матрица расстояний, размерность которой снижается на единицу.

Компонентный анализ предназначен для преобразования системы k исходных признаков в систему k новых показателей (главных компонент). Главные компоненты не коррелированны между собой и упорядочены по величине их дисперсий, причем первая главная компонента имеет наибольшую дисперсию, а последняя, k – я, - наименьшую.

В задачах снижения размерности и классификации обычно используется m первых компонент ( ). При наличии результативного показателя Y может быть построено уравнение регрессии на главных компонентах.

Для простоты изложения алгоритма ограничимся случаем трех переменных.

На основании матрицы исходных данных

, (5.6)

вычисляем оценки параметров распределения трехмерной генеральной совокупности , , , где = ; ;

; . (5.7)

Получаем оценку матрицы парных коэффициентов корреляции: .

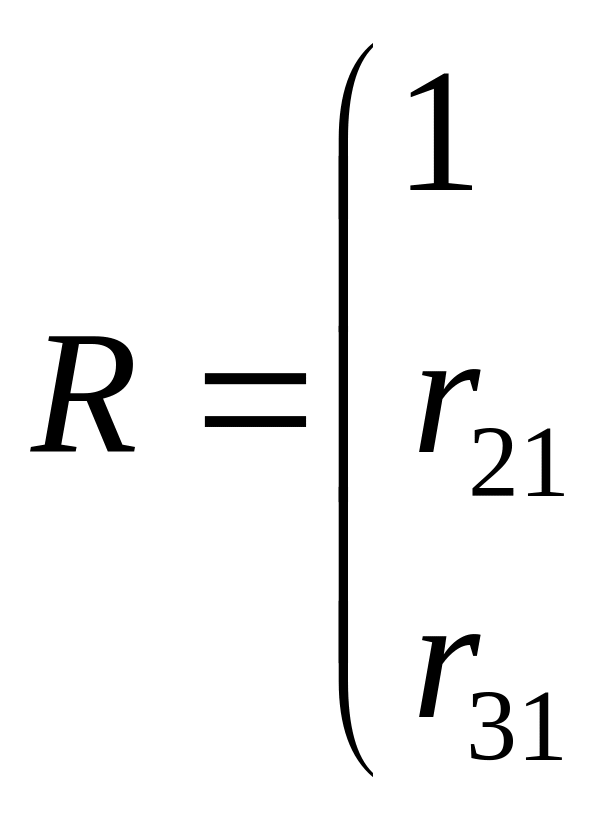
Преобразуем матрицу R в диагональную матрицу собственных значений характеристического многочлена .

Характеристический многочлен имеет вид

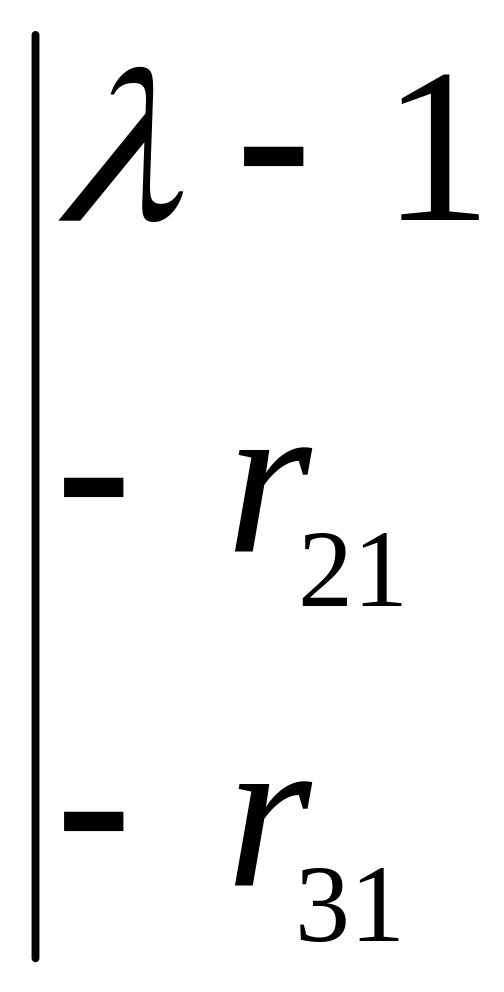
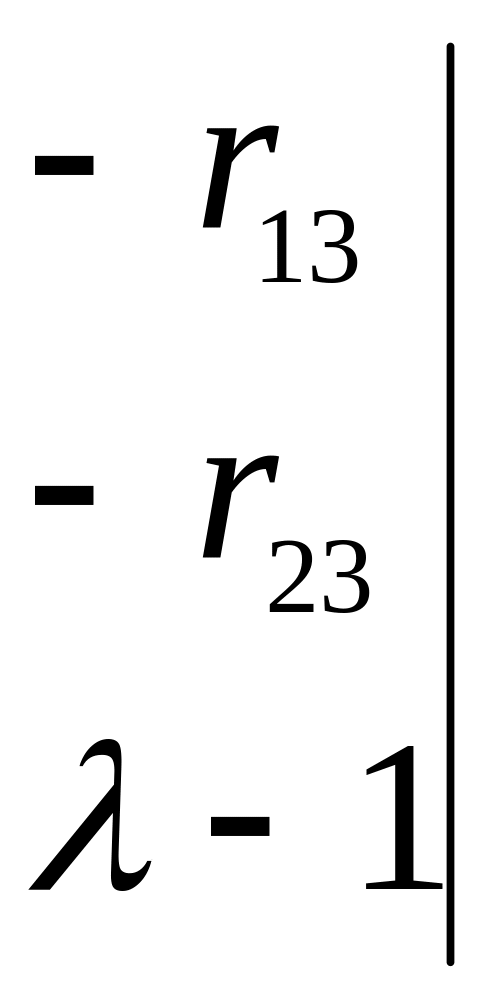= = , (5.8)

где E – единичная матрица.

Приняв , получим неполное кубическое уравнение , (5.9)

где , .

Решая это уравнение и учитывая выполнение неравенства <0, получим: , , (5.10)

где 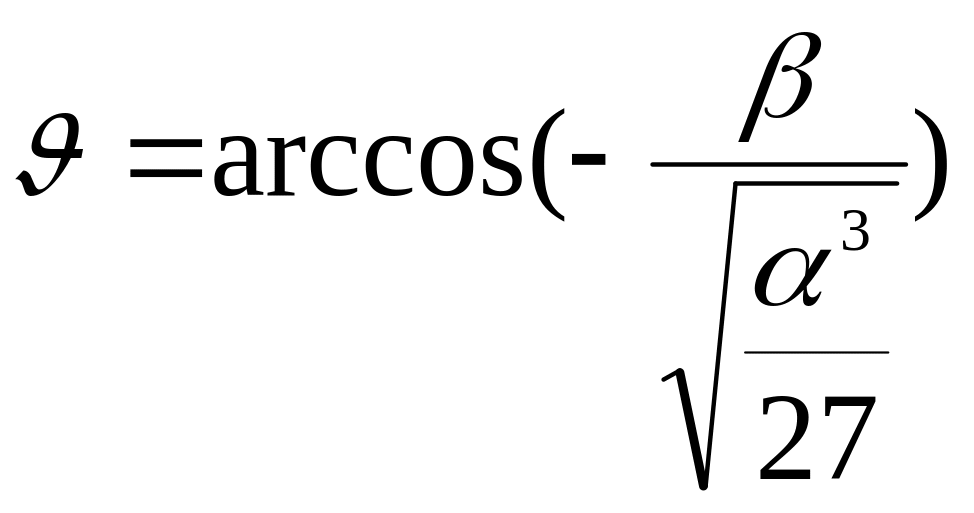. (5.11)

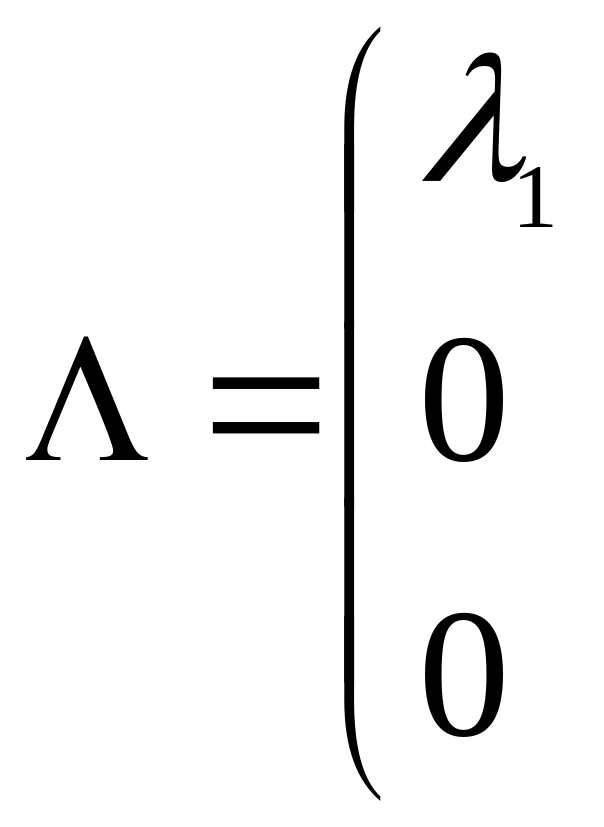
Отсюда получаем собственные значения , причем и матрицу собственных значений . (5.12)

Собственные значения характеризуют вклады соответствующих главных компонент в суммарную дисперсию исходных признаков . Таким образом, первая главная компонента оказывает наибольшее влияние на общую вариацию, а третья – наименьшее. При этом должно выполняться равенство . Вклад l-й главной компоненты в суммарную дисперсию определяется по формуле .

Найдем теперь матрицу преобразования V - ортогональную матрицу, составленную из собственных векторов матрицы R. Собственный вектор , отвечающий собственному числу , находим как отличное от нуля решение уравнения . Так как определитель =0, то можно считать, что третья строка есть линейная комбинация первых двух строк. Составим два уравнения

(5.13)

Примем и получим решение системы двух уравнений с двумя неизвестными.

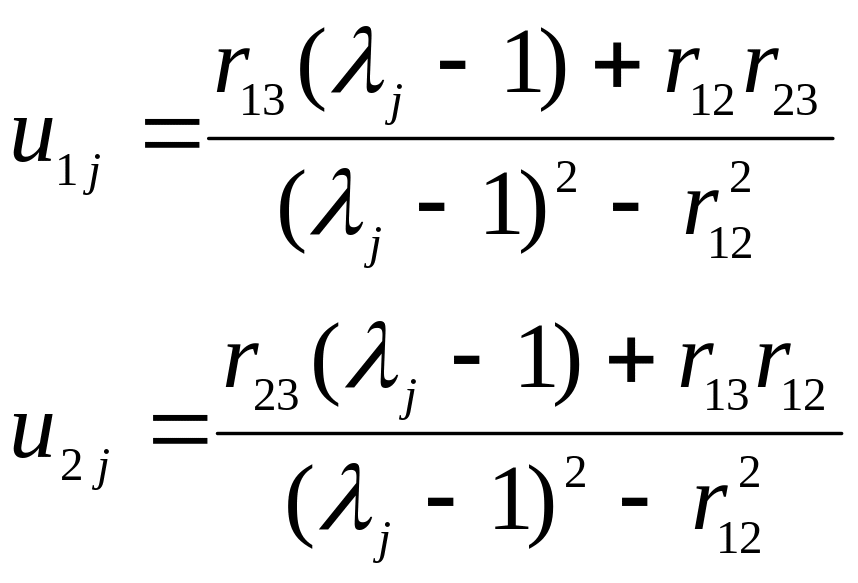(5.14)

Тогда окончательно собственный вектор имеет вид

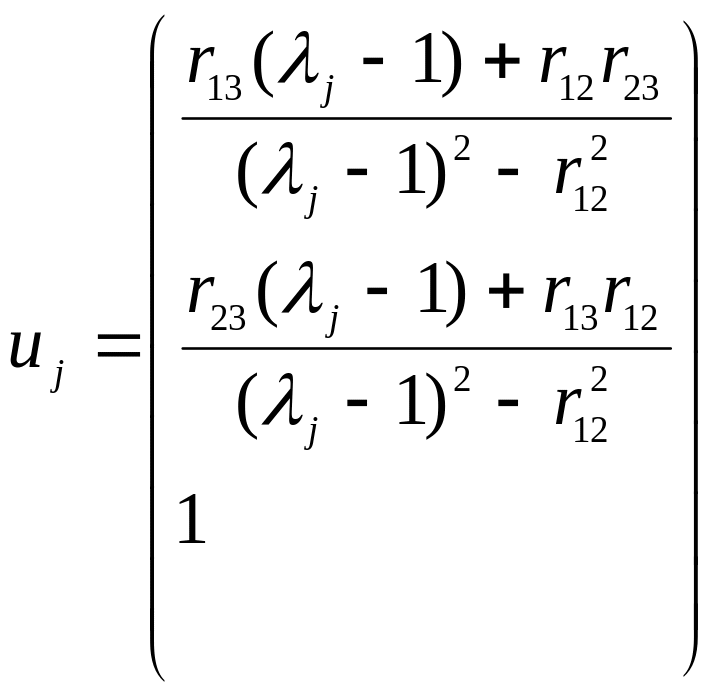для j=1,2,3. (5.15)

Находим норму вектора . Тогда матрица V, составленная из нормированных векторов 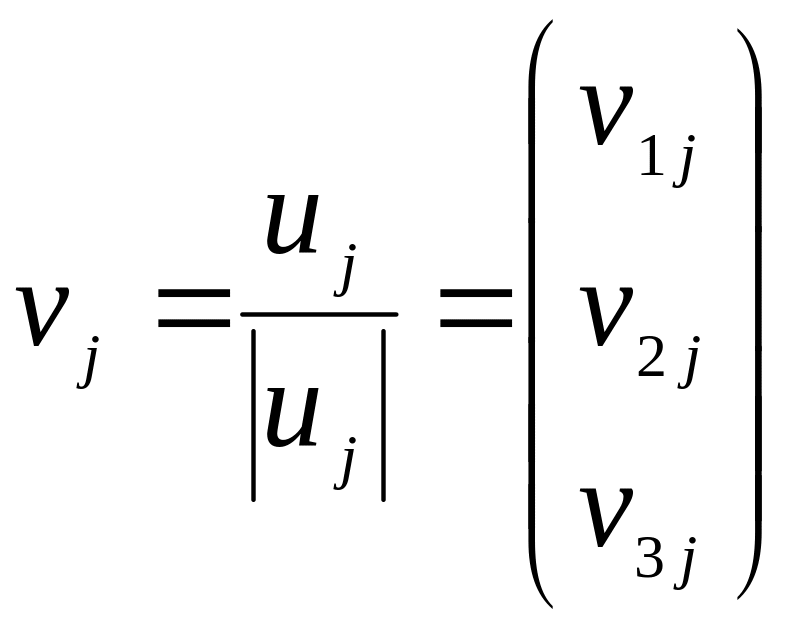, (5.16)

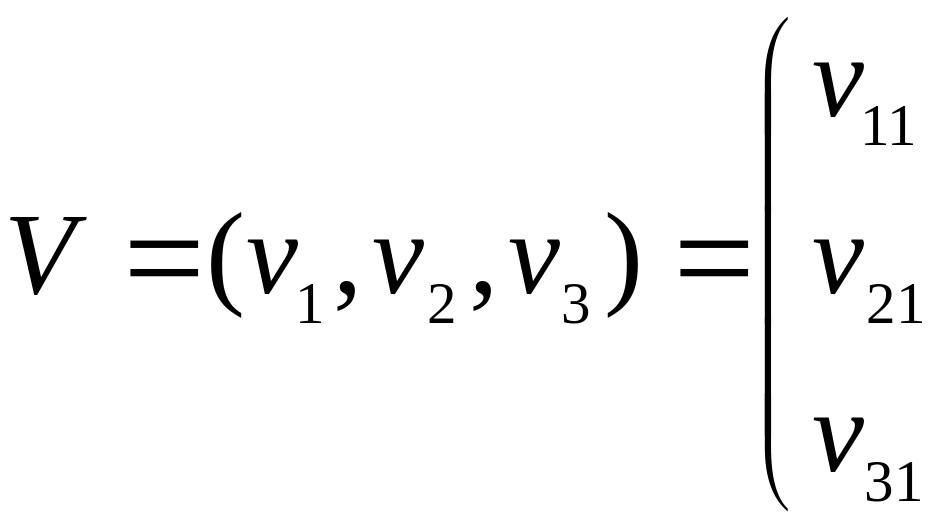
имеет вид (5.17)

и является ортогональной .

Матрица факторных нагрузок получается по формуле

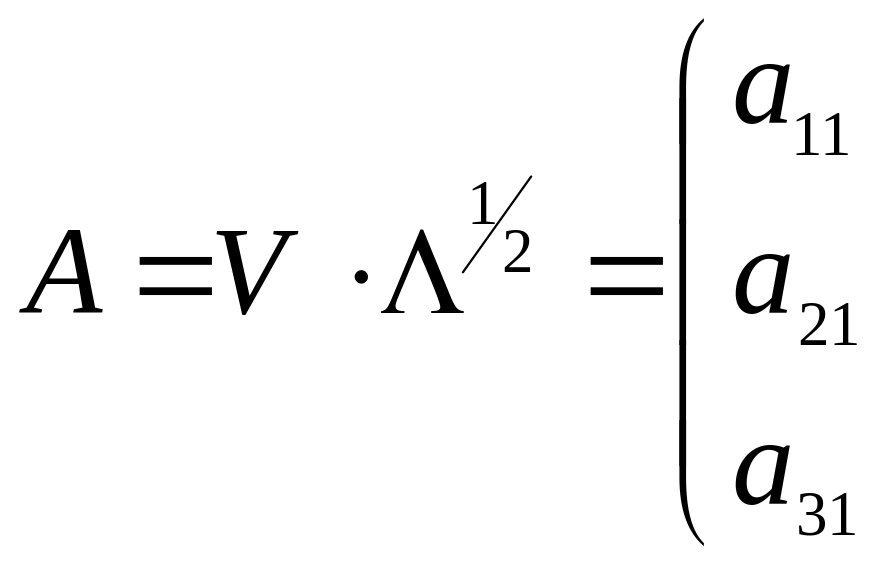
, (5.18)

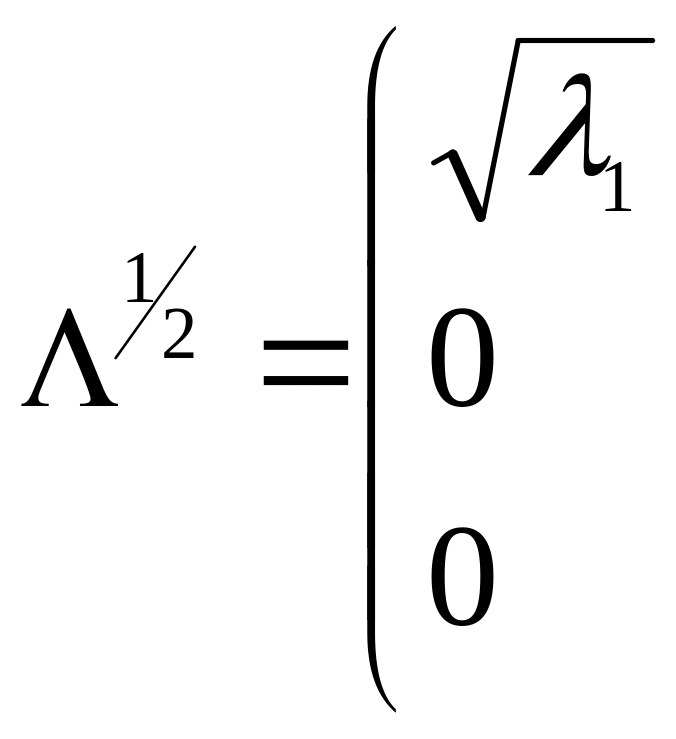
где - диагональная матрица: (5.19)

Таким образом, нагрузка l-й главной компоненты на j-ю переменную вычисляется по формуле: ; j =1,2,3; l=1,2,3.

Элемент матрицы факторных нагрузок есть коэффициент корреляции, который измеряет тесноту связи между l-й главной компонентой и -м признаком . При этом имеет место соотношение: .

Матрица факторных нагрузок A используется для экономической интерпретации главных компонент, которые представляют собой линейный функции исходных признаков. Значения главных компонент для каждого i-объекта задаются матрицей F. Матрицу значений главных компонент можно получить по формуле:

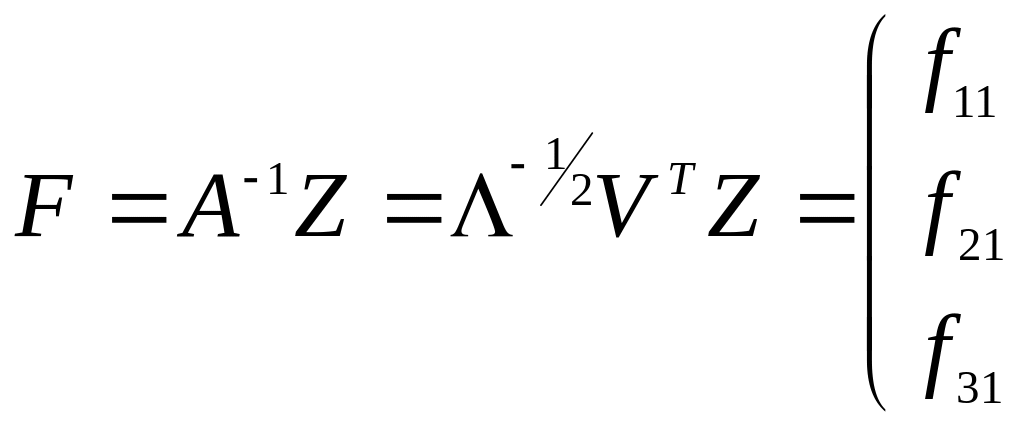
, где (5.20)

Z- матрица нормированных значений наблюдаемых переменных размером .

Таким образом, значения главных компонент получаем из выражения

, (5.21)

где , ; l=1,2,3.

Полученные главные компоненты позволяют классифицировать множество исходных признаков на группы, обобщающими показателями которых и являются главные компоненты. В силу ортогональности (независимости) главные компоненты удобны для построения на них уравнения регрессии ввиду отсутствия мультиколлинеарности главных компонент. Для построения уравнения регрессии на главных компонентах в качестве исходных данных следует взять вектор наблюдаемых значений результативного признака y и вместо матрицы значений исходных показателей X – матрицу вычисленных значений главных компонент F.

69