Дисперсией случайной величины х называется число dx , равное математическому ожиданию квадрата отклонения случайной величины от своего математического ожидания: . (1.4)
Если известен
закон распределения случайной величины
Х,
то для дискретной и непрерывной случайных
величин дисперсию можно вычислить
соответственно по формулам:
(1.5)
,
(1.6)
где - плотность распределения случайной величины.
В качестве меры
рассеивания случайной величины наряду
с дисперсией используют среднеквадратическое
отклонение
,
равное квадратному корню из дисперсии
случайной величины:
=
. (1.7)
Среднеквадратическое отклонение случайной величины выражается в тех же единицах, что и сама случайная величина и ее математическое ожидание.
Приведем без доказательств основные свойства дисперсии. Свойства среднеквадратического отклонения непосредственно вытекают из соответствующих свойств дисперсии.
Дисперсия постоянной с равна нулю: D(c)=0.
2) Дисперсия
произведения случайной величины Х
на постоянную с
равна произведению дисперсии случайной
величины Х
на квадрат постоянной:
.
Если случайные величины X иY независимы, то дисперсия их суммы равна сумме их дисперсий:
.
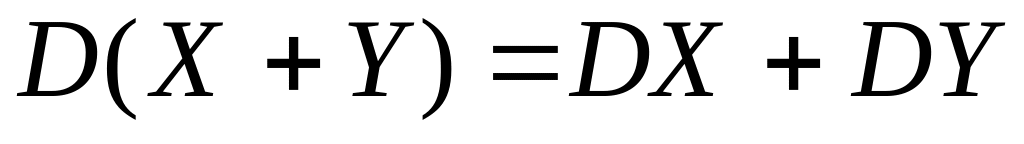4) Дисперсия
случайной величины Х
не изменится, если к ней прибавить
постоянную с,
т.е.
.
Моменты случайной величины обобщают понятия математического ожидания и дисперсии.
Моментом k – порядка называется математическое ожидание k –й степени отклонения случайной величины Х от некоторой постоянной с.
Если в качестве с берется нуль, моменты называют начальными, то есть
. (1.8)
Если с=М(Х), то моменты называются центральными, то есть
. (1.9)
Таким образом, математическое ожидание – ни что иное, как первый начальный момент, а дисперсия – второй центральный момент.
Существует формула, связывающая центральные моменты с начальными:
. (1.10)
Для первых четырех моментов эта формула дает следующие равенства:
(1.11)
Формула
может
быть использована для нахождения
дисперсии случайной величины:
(1.12)
В теории и
практических приложениях используют
две числовые характеристики случайной
величины, основанные на центральных
моментах третьего и четвертого порядков
соответственно – коэффициент асимметрии
и эксцесс
.
Данные коэффициенты дают представление
о форме плотности распределения или
многоугольника распределения.
Коэффициентом
асимметрии случайной величины Х
называется число, равное отношению
третьего центрального момента к кубу
среднеквадратического отклонения
случайной величины
Х:
(1.13)
Коэффициент
асимметрии случайной величины, закон
распределения которой симметричен
относительно математического ожидания,
равен нулю, поскольку в этом случае
.
Если распределение вероятностей
несимметрично, причем «длинная часть»
распределения расположена справа от
центра группирования, то
>0
и асимметрию называют положительной,
если же «длинная часть» расположена
слева, то
<0
и асимметрию называют отрицательной.
В качестве характеристики большей или меньшей степени «сглаженности» плотности или многоугольника распределения по сравнению с нормальной плотностью используют понятие эксцесса. Эксцессом случайной величины Х называется число, равное разности отношения четвертого центрального момента к четвертой степени среднеквадратического отклонения случайной величины и числа 3:
(1.14)
Эксцесс нормального закона распределения вероятностей равен нулю. Если распределение вероятностей случайной величины Х одномодально и плотность распределения более «островершинна», чем плотность распределения нормальной случайной величины с той же дисперсией, то >0, если же менее «островершинна» и более «сглажена» по сравнению с плотностью соответствующего нормального распределения, то <0.
В математической
статистике широко используются понятия
q-квантилей
и
Q-процентных
точек
распределения
F(x).
Квантилью
уровня q
(или q-квантилью)
непрерывной случайной величины Х,
обладающей
непрерывной функцией распределения
F(x),
называется такое возможное значение
этой
случайной величины, для которого
вероятность события Х
<
равна
заданной величине q,
т.е.
.
(1.15)
Очевидно, чем
больше заданное значение q
(0<q<1),
тем больше будет и соответствующая
величина квантили
.
Частным случаем квантили - 0.5 –квантилью
является характеристика центра
группирования - медиана.
Для дискретной
случайной величины функция q-квантиль
определяется как любое число
,
лежащее между двумя значениями
и
,
такими, что
<
q,
но
q.
Под
Q-процентной
точкой
(0< Q<100)
случайной величины Х
понимается такое ее возможное значение
,
для которого вероятность события Х
,
равна Q/100:
.
(1.16)
Для дискретной случайной величины это определение корректируется аналогично тому, как это делалось при определении квантилей.
Между квантилями
и процентами точками существует следующее
соотношение:
.
Нормальное распределение (закон Гаусса) занимает центральное место в теории и практике статистических исследований. Распределение задается плотностью:
,
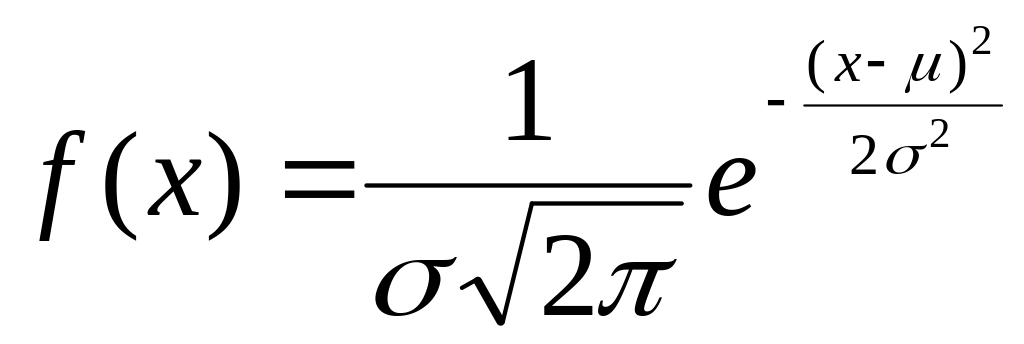(1.17)
где
- математическое ожидание;
- среднеквадратическое отклонение.
Кривая нормального
распределения симметрична относительно
прямой, параллельной оси ординат и
проходящей через точку
,
и имеет в этой точке единственный
максимум, равный
.
С уменьшением
кривая становится более вытянутой по
отношению к прямой
.
Изменение
при постоянном
не
меняет формы кривой, а вызывает лишь ее
смещение вдоль оси абсцисс. Таким
образом, нормальное распределение
зависит от двух параметров:
и
.
Площадь, заключенная под кривой
нормального распределения, равна
единице. Коэффициент асимметрии и
эксцесс равны нулю.
Логарифмически-нормальное
распределение
(логнормальное распределение) –
распределение положительной случайной
величины, логарифм которой распределен
по нормальному закону. Таким образом,
если случайная величина Х
распределена по нормальному закону, то
случайная величина
имеет
логнормальное распределение. Распределение
является асимметричным.
Плотность вероятности задается следующим выражением:
.
(1.18)
Математическое ожидание и дисперсия определяются по следующим формулам:
;
(1.19)
,
(1.20)
где - математическое ожидание Х; - среднеквадратическое отклонение Х.
Биномиальное распределение – распределение вероятностей дискретной случайной величины X=m, принимающей значение 0,1,2,…, n и задаваемой функцией вероятностей :
,
(1.20)
где
- вероятность появления события А
m
раз в n
независимых испытаниях, в каждом из
которых событие А
появляется с одно и той же вероятностью
p
и не появляется с вероятностью
;
- число сочетаний
из n
по
m.
Параметрами распределения являются величины n и р. Математическое ожидание и дисперсия задаются следующим образом:
(1.21)
Равномерное
распределение
– распределение вероятностей непрерывной
случайной величины на каком-либо отрезке
,
где
,
имеющее плотность:
при
(1.22)
Математическое ожидание и дисперсия соответственно равны:
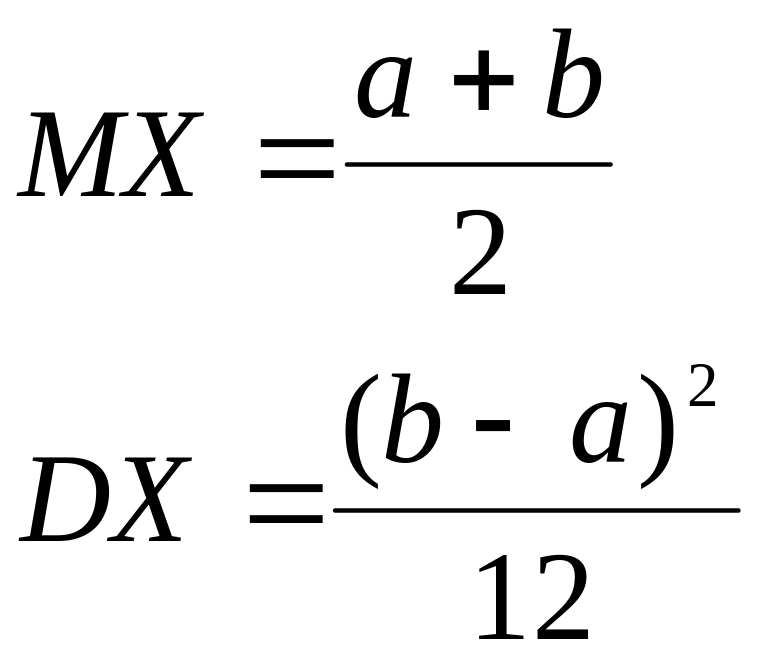(1.23)