Методические указания, задачи и упражнения по темам

Тема 1. Теория вероятностей и математическая статистика – основной инструментарий для прикладной статистики

Случайная величина – переменная величина, принимающая одно из возможных значений в зависимости от случайных обстоятельств. Случайная величина считается полностью заданной своим распределением, если указан закон, по которому можно вычислить вероятность попадания случайной величины в любое подмножество ее возможных значений.

Распределение вероятностей – совокупность всех возможных значений случайной величины и соответствующих им вероятностей.

Случайная величина называется дискретной, если она принимает конечное или счетной число значений. Дискретная величина задается с помощью ряда распределения – функции, ставящей в соответствие каждому возможному значению случайной величины определенную вероятность. Таким образом, ряд распределения - это конечное или счетное множество пар элементов:

Так как случайная величина Х примет обязательно какое-нибудь из своих значений , сумма вероятностей всех возможных значений равно единице, т.е. для случайной величины, принимающей конечное число n возможных значений, и для дискретной случайной величины, принимающей счетное число значений.

Обычно ряд распределения удобно изображать в виде таблицы, где в верхней строке указаны возможные значения дискретной случайной величины Х, в нижней – соответствующие вероятности того, что Х примет значение .

Х= .

Полигоном (многоугольником) распределения называется графическое изображение ряда распределения. Для того чтобы построить полигон распределения необходимо отложить возможные значения случайной величины по оси абсцисс, а соответствующие им вероятности по оси ординат.

Множество значений непрерывной случайной величины несчетно и обычно представляет собой некоторый промежуток, конечный или бесконечный. Непрерывная величина принимает возможные значения, заполняющие сплошь заданный интервал, причем для любого х из этого интервала существует предел:

Функция называется плотностью распределения или дифференциальным законом распределения.

Плотность распределения обладает следующими свойствами:

1) ;

2. Для любых 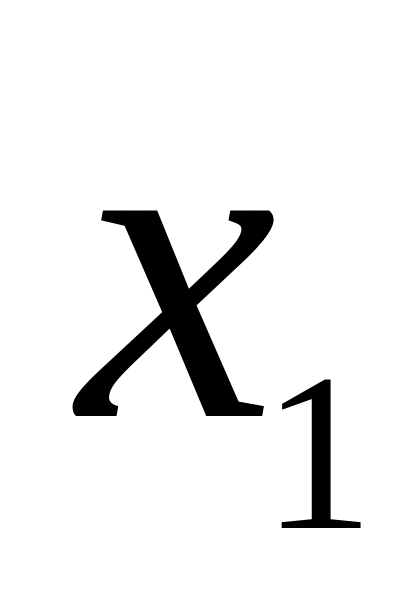< 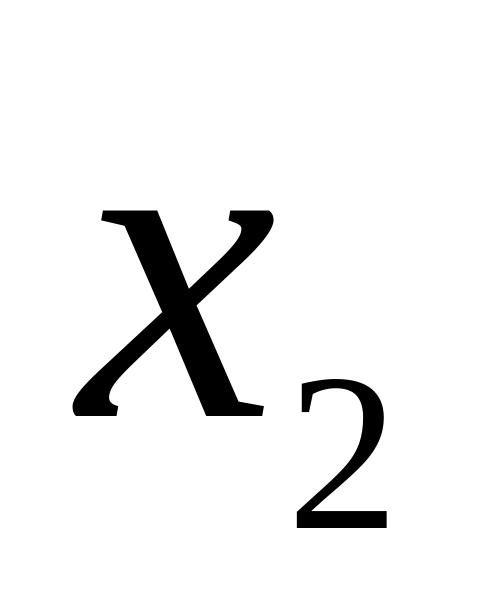выполняется равенство: =

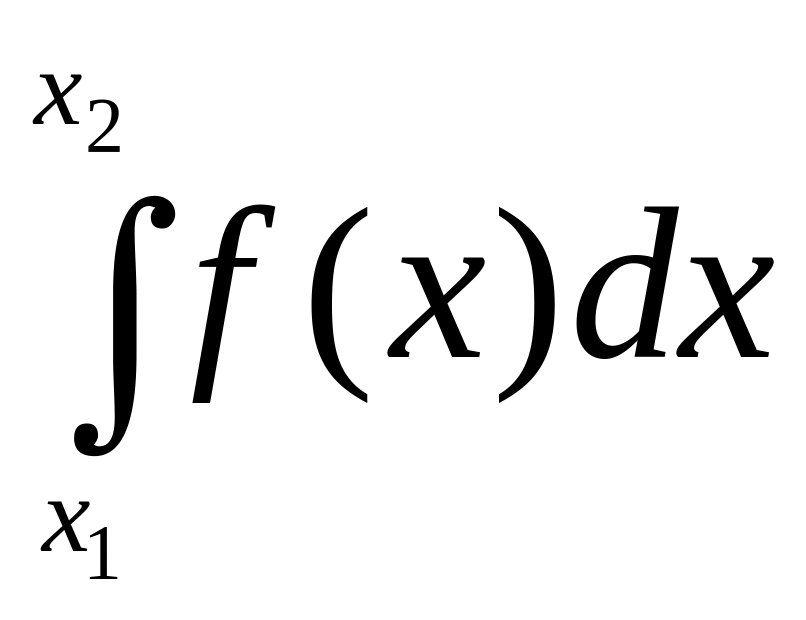
3. Интеграл по всей числовой прямой от плотности распределения вероятностей равен 1, т.е. .

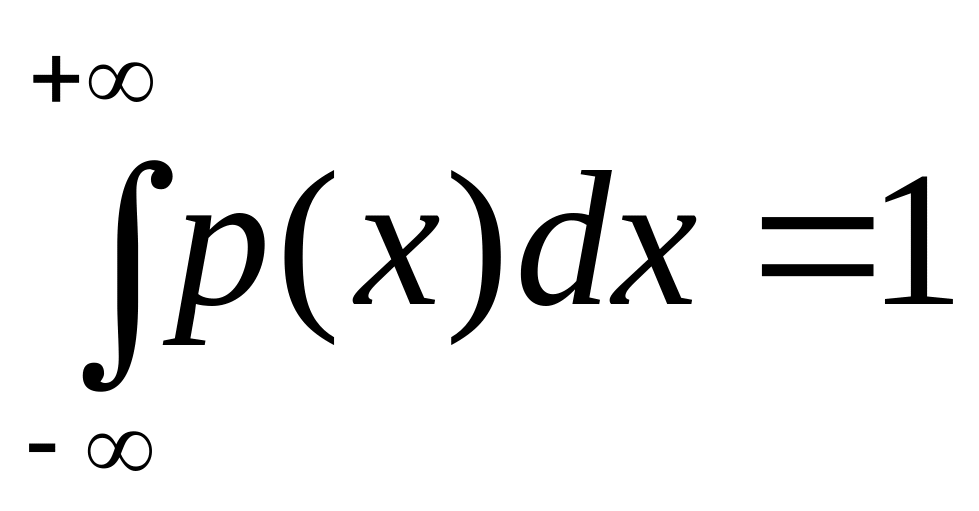4. Вероятность того, что непрерывная случайная величина примет конкретное значение, равна 0, т.е. .

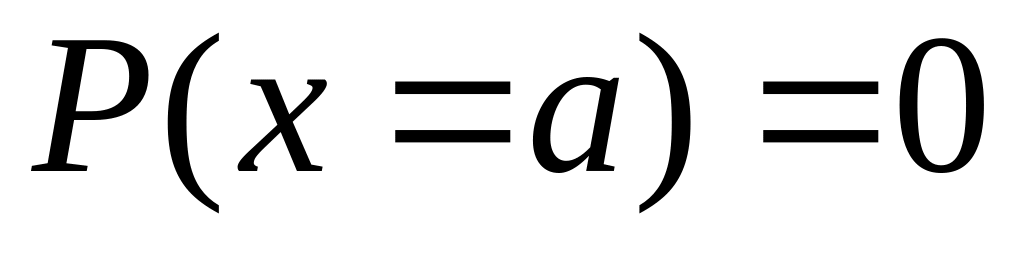График плотности распределения носит название кривой распределения.

Функцией распределения F(x) случайной величины Х, принимающей любое действительное значение x, называется вероятность того, что случайная величина Х приимет значение меньшее чем х, то есть . Функцию распределения F(x) называют также интегральным законом распределения.

Для дискретной случайной величины функция F(x) вычисляется по формуле:

,

где суммирование осуществляется по всем значениям i, для которых .

Для непрерывной случайной величины интегральный закон выражается формулой: , где функция - плотность распределения.

Функцией распределения F(x) обладает следующими свойствами:

1) = F(x₂) – F(x₁);

2) , если ;

3) ;

4) ;

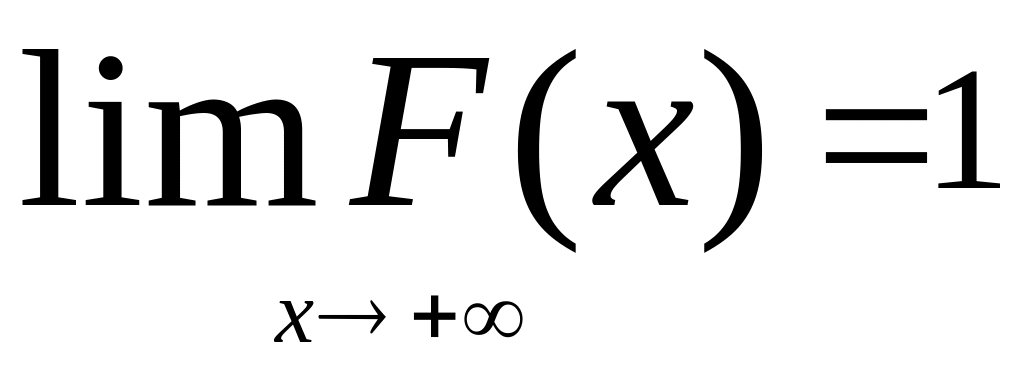5) (для непрерывной случайной величины).

График функции распределения F(x) для непрерывных случайных величин называется интегральной кривой распределения.

Числовые характеристики случайных величин. Функция распределения дает полную информацию о законе распределения случайной величины. Однако часто бывает достаточно знать одну или несколько числовых характеристик случайной величины, дающих наглядное представление о ней, например, некоторое «среднее» число, вокруг которого группируются значения случайной величины (центр группирования распределения), и ту или иную характеристику вариации значений случайной величины (степень рассеивания ее значений).

Основной характеристикой центра группирования случайной величины в генеральной совокупности является ее математическое ожидание. Выборочным аналогом математического ожидания является среднее значение .

Математическое ожидание М(х) дискретной случайной величины определяется по формуле: (1.1)

Если случайная величина Х непрерывна и - ее плотность распределения, то математическим ожиданием называется интеграл:

, (1.2)

в тех случаях, когда существует интеграл .

Приведем без доказательств основные свойства математического ожидания.

1. Математическое ожидание постоянной равно этой постоянной, т.е. если с – постоянная, то М(Х)=с .

2. Постоянную величину можно выносить за знак математического ожидания, т.е. если Х – случайная величина, а с – постоянная, то М(сХ)=с*М(Х).

3. Математическое ожидание суммы случайных величин равно сумме математических ожиданий этих случайных величин, т.е. если определены МХ и МY, то определено математическое ожидание М(Х+Y), причем М(Х+Y)= МХ+ МY. Это свойство верно как для зависимых, так и независимых случайных величин.

4. Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий этих случайных величин, т.е. если Х и Y – независимые случайные величины, то М(ХY)= МХ* МY.

Модальное значение (или просто мода) Мо случайной величины определяется как такое возможное значение исследуемого признака, при котором значение плотности вероятности (в непрерывном случае) или вероятности (в дискретном случае) достигает своего максимума. Мода представляет собой наиболее часто встречающееся значение случайной величины.

Медиана Ме исследуемого признака определяется как его средневероятное значение, т.е. такое значение, которое обладает следующим свойством: вероятность того, что случайная величина окажется больше Ме , равна вероятности того, что она окажется меньше. Для обладающих непрерывной плотностью случайных величин выполняется условие:

(1.3)

и медиану можно определить как такое значение на оси абсцисс, при котором прямая, параллельная оси ординат и проходящая через точку делит площадь под кривой плотности на две равные части. В некоторых случаях дискретных распределений может не существовать величины, точно удовлетворяющей сформулированному требованию. Поэтому для дискретных величин медиану можно определить как любое , лежащее между соседними возможными значениями и , такими, что <0,5 и 0,5.

Характеристики вариации уточняют представление о распределении вероятностей случайной величины. Они дают представление о степени рассеивания случайной величины относительно центра группирования. Наиболее часто используемыми характеристиками вариации являются дисперсия случайной величины и ее среднеквадратическое отклонение.