Определение тройного интеграла и его геометрический смысл:

Пусть в замкнутой кубируемой области V пространства XYZ задана произвольная функция Разобьем область V на n областей не имеющих общих внутренних точек. В каждой точке области возьмем произвольно точку Значение функции в точке умножим на объем i-й области и сложим такие произведения по всем областям деления. Полученная сумма называется интегральной суммой для функции по области V. Для функции можно составить бесчисленное множество интегральных сумм по области V. Таким образом, если этот предел существует.

Из определения следует, что тройной интеграл, так же как и двойной, не зависит от совершаемых при построении интегральных сумм разбиения области V на части и выбора точек на этих частях.

Тройные интегралы являются непосредственным обобщением двойных интегралов на случай трехмерного пространства.

Вычисление тройного интеграла в декартовых координатах:

Пусть область D - правильная в отношении оси Ох

Тогда в этом случае область D может быть задана одной системой неравенств:

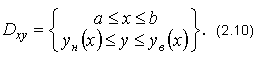
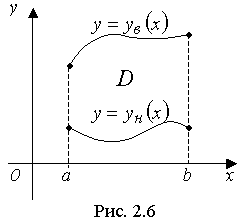
Если существует двойной интеграл

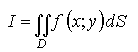
(это возможно, например, если f(x; y) непрерывна на D), то его можно вычислить через повторный кратный интеграл так:

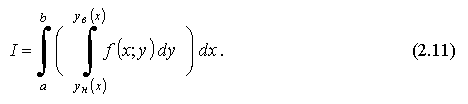
При этом внутренний интеграл по у находится при постоянном х.

Данное представление (2.11) получается из определения двойного интеграла при специальном способе разбиения области D на n "мелких" частей (линиями, параллельными либо Ох, либо Оу - прямоугольной "шахматной" сеткой. А затем выполняется суммирование "объёмов" ΔVi сначала по оси Оу, а затем по оси Ох).

Замена переменных в тройном интеграле:

Для тройного интеграла имеет место следующее правило замены переменных.

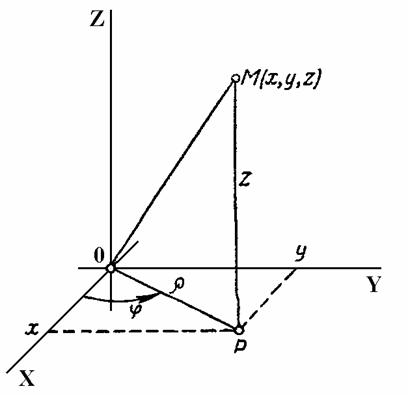
Если функция непрерывна в замкнутой области V, а функции

имеют непрерывные частные производные в замкнутой области Т пространства UVW и взаимно однозначно отображают эту область на область V пространства XYZ, то имеет место следующая формула:

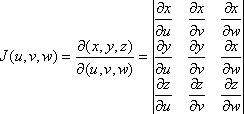якобиан отображения

Подобно тому как в случае двух переменных модуль якобиана отображения равнялся коэффициенту изменения бесконечно малой площади, модуль якобиана отображения (1) равен коэффициенту изменения бесконечно малого объема при отображении (1).

приложения тройного интеграла:

Объем тела

Масса тела

( - плотность тела).

Координаты центра масс

..............криволинейные интегралы первого и второго родов

криволенейный интеграл первого рода

Пусть l — гладкая, без особых точек и самопересечений кривая (допускается одно самопересечение — случай замкнутой кривой), заданная параметрически.

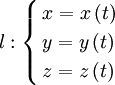
(отрезок параметризации) – рассматриваем часть кривой.

Пусть – разбиение отрезка параметризации причем

Зададим разбиение кривой:

За обозначим часть кривой от точки до точки

http://ru.wikipedia.org/wiki/Криволинейный_интеграл

определение криволинейного интеграла первого рода:

http://matclub.ru/lec17/lec2.htm

вычисление криволинейного интеграла первого рода:

Выберем на кривой L направление от начальной точки А и отметим, что положение точки М на кривой определяется длиной дуги АМ = s. Тогда кривую L можно задать параметрически: x = x(s), y = y(s), z = z(s), где Функция f(x,y,z) становится при этом сложной функцией одной переменной s: f(x(s), y(s), z(s)). Тогда интегральная сумма где - координата точки Mi, является обычной интегральной суммой для определен-ного интеграла Следовательно,

Таким образом, вычисление криволинейного интеграла 1-го рода сводится к вычислению обычного определенного интеграла от функции переменной t в пределах, соответствующих изменению значения этой переменной на рассматриваемой кривой.

Пример. Вычислить где L 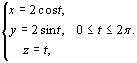Применяя формулу

получим: