5. 5. Застосування подвійного інтеграла в геометрії Площа плоскої фігури.

На підставі властивостей подвійного інтеграла .

Для підінтегральна функція і виходячи з геометричного змісту подвійного інтеграла одержимо об'єм циліндричного тіла висотою , що дорівнює площі основи тіла, тобто (од. куб.) = (од. кв.).

Отже, у прямокутних координатах

. (6.9)

У полярній системі координат , тому

. (6.10)

Рис. 6.11.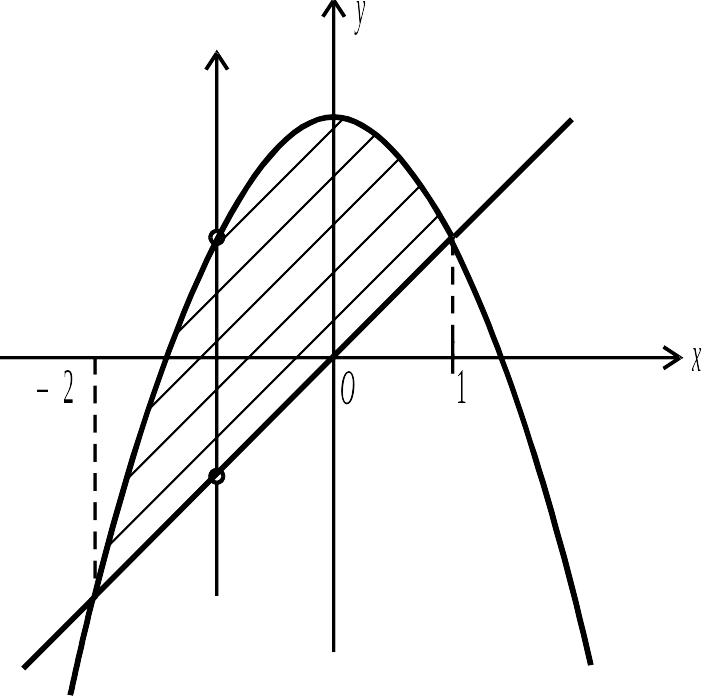

Приклад 6.4. Обчислити площу фігури, що обмежена лініями , (рис. 6.11).

Розв’язання. Розглянемо область як просту відносно і запишемо її нерівностями. Для цього знайдемо точки перетину ліній, що обмежують область (крайні точки області по вісі ), розв’язавши систему рівнянь

Отже,

Тоді

Приклад 6.5. Обчислити площу фігури, що обмежена лініями , , , .

Розв’язання. Перетворимо перші два рівняння до канонічного вигляду, одержимо , . Перше рівняння визначає коло з центром у точці (1;0) з радіусом , друге рівняння також визначає коло з центром у точці (2;0) з радіусом (рис. 6.12).

Рис. 6.12.

Як видно з рисунка, дану площу не можна обчислити за допомогою одного подвійного інтеграла в прямокутних координатах.

В полярній системі координат область є простою по . Рівняння кіл, що обмежують область у полярній системі координат, одержимо, підставивши в їхні початкові рівняння , . Тоді рівняння першого кола набуде вигляду , а для другого відповідно .

Очевидно, що

Тоді

(кв. од.)

Об'єм тіла.

Виходячи з геометричного змісту подвійного інтеграла, об'єм тіла з основою в площині , бічною поверхнею, паралельною вісі , обмеженого зверху поверхнею заданою рівнянням , може бути обчислений за формулою

. (6.10)

Приклад 6.6. Знайти об'єм тіла , обмеженого поверхнями , , , (рис. 6.13).

Розв’язання. Дане тіло є циліндричним з основою у площині , обмеженим зверху параболоїдом . Отже, .

В силу симетричності тіла відносно координатної площини можна обчислити об'єм тіла з основою , (рис. 6.14), потім результат подвоїти.

Рис. 6.13.	Рис. 6.14.

Оскільки

Приклад 6.7. Обчислити об'єм тіла, обмеженого поверхнями , , z=0 (рис. 6.15).

Рис. 6.15.

Розв’язання. Оскільки основою тіла в площині є область, обмежена колом , обчислимо об'єм, використовуючи полярну систему координат. Зверху тіло обмежене поверхнею , рівняння якої в полярній системі координат . Тому ,

де .

Тоді . Область можна записати за допомогою нерівностей

Отже .

Площа поверхні.

Розглянемо поверхню, задану рівнянням . Нехай їх відповідає область площини . Тоді площа поверхні може бути обчислена за формулою

. (6.11)

6. 6. Застосування подвійного інтеграла у фізиці Маса плоскої пластини.

Розглянемо тонку пластину, розташовану в площині, яка займає область . Товщину цієї пластинки вважаємо настільки малою, що зміною щільності за товщиною можна знехтувати.

Поверхневою щільністю такої пластинки в даній точці називається границя відношення маси елементарної ділянки, що містить цю точку, до її площі за умови, що площа ділянки стягується до даної точки. Позначимо щільність , маємо

.

Якщо стала в кожній точці області, то маса обчислюється за формулою , де – площа пластинки.

Нехай пластинка неоднорідна, тобто .

Розіб'ємо область , що займає пластинка, на елементарних ділянок. У кожній ділянці розбивання довільно виберемо точу і будемо вважати, що щільність елементарної пластинки стала і така, як в обраній точці, тобто .

Тоді масу кожної елементарної ділянки можна вважати приблизно рівною

.

Масу всієї пластинки одержимо, якщо додамо маси елементарних ділянок:

.

Точний результат знайдемо, перейшовши в останній рівності до границі:

. (6.12)

Формулу (6.12) можна розглядати як механічний зміст подвійного інтеграла: подвійний інтеграл дорівнює масі плоскої пластини, що займає область , якщо щільність розподілу маси в цій області дорівнює підінтегральній функції .