Часть III.

Вам предлагаются 5 заданий. На каждое из заданий Вы можете дать ответ в виде положительного или отрицательного числа заполнив соответствующую номеру вопроса строчку в бланке ответов. В каждой клетке строки может располагаться только один символ: цифра, знак « - »отрицательного числа, или знак « . » разделителя десятичной дроби. Вы можете дать ответ не «Не знаю», оставив все пять соответствующих вопросу клеток пустыми.

В этой части за каждое правильно выполненное задание дается три балла, в противном случае баллы не начисляются.

Задание 1. Вычислить предел

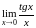
Решение. Используя первый замечательный предел 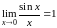, находим

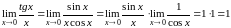
Ответ: 1.

Задание 2. Найти точку минимума функции .

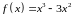Решение. В точке функция достигает экстремума - минимума (максимума), если для любых из некоторой окрестности точки выполняется неравенство .

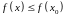
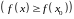Во всех точках экстремума производная функции равна нулю или не существует.

Пусть функция дифференцируема в некоторой окрестности точки , кроме, быть может, самой точки, и непрерывна в точке . Если производная функции меняет знак с минуса на плюс при переходе через точку слева направо, то точка минимума. Если производная функции меняет знак с плюса на минус при переходе через точку слева направо, то точка максимума.

Для функции производная равна

.

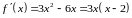Определяем знаки производной:

Ответ: 2.

Задание 3. Найти значение функции 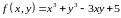в точке локального экстремума.

Решение. Точка 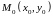является точкой максимума (минимума) функции , если найдется такая окрестность точки 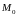, что для всех точек из этой окрестности выполняется неравенство .

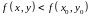
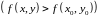Точки максимума и минимума называются точками экстремума. При этом если в точке экстремума существует первая частная производная, по какому-либо аргументу, то она равна нулю.

Точки экстремума дифференцируемой функции, то есть функции, имеющей непрерывные частные производные во всех точках некоторой области, надо искать только среди тех точек, в которых все первые частные производные равны нулю.

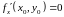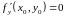Пусть и , а вторые частные производные функции непрерывны в некоторой окрестности точки 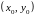. Введем обозначения:

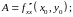
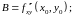
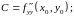
Тогда, если 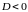, то в точке экстремума нет.

Если 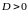, то в точке экстремум функции есть, причем если 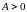, то минимум, а если 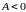, то максимум.

Если , то экстремум может быть, а может и не быть. В данном случае требуются дополнительные исследования.

Для функции находим первые частные производные:

,

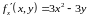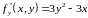
и решаем систему

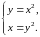
Тем самым находим точки подозрительные на экстремум: 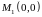и .

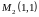Находим вторы частные производные и смешанную производную:

, , .

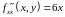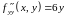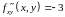Определяем знак выражения 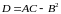в каждой точке подозрительной на экстремум

.

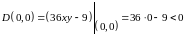Следовательно, в точке экстремума нет.

.

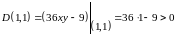Поэтому в точке есть экстремум.

Находим значение функции в точке :

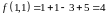
Ответ: 4.

Задание 4. Вычислить определенный интеграл: .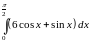

Решение. Значение определенного интеграла может быть вычислено по формуле Ньютона-Лейбница: определенный интеграл от непрерывной функции равен разности значений первообразной функции на верхнем и нижнем пределах

.

Поэтому

.

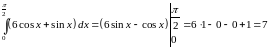Ответ: 7.

Задание 5. Найти площадь 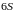фигуры 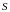ограниченной параболой 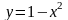и прямой .

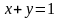Решение. Площадь этой фигуры записывается с помощью интеграла как 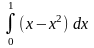, поэтому

.

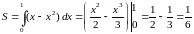Следовательно

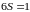
Ответ: 1.