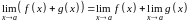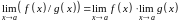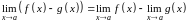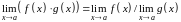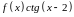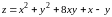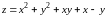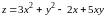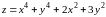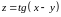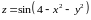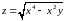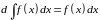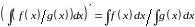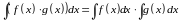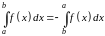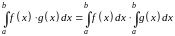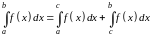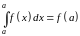ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ЭКОНОМИКИ И ФИНАНСОВ»
Кафедра высшей математики
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ДЛЯ ПОДГОТОВКИ
К ЭКЗАМЕНУ ПО МАТЕМАТИКЕ
ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ОТДЕЛЕНИЯ
Раздел: математический анализ
ИЗДАТЕЛЬСТВО
САНКТ-ПЕТЕРБУРСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА
ЭКОНОМИКИ И ФИНАНСОВ
2011 г.
Методические указания и контрольные задания по курсу «Математики» Раздел: математический анализ для студентов вечернего и заочного факультетов. – СПб.: Изд-во СПбГУЭФ, 2011.- 32с.
Методические указания составлены в соответствии с учебной программой курса «Математика» раздела «Математический анализ» и предназначены для студентов первого курса вечернего и заочного факультетов. В данном пособии приведены контрольные задания для самостоятельной работы и даны указания по их решению.
Автор-составитель: Матвеев П. Н.
Рецензент: к.ф.-м.н., доцент Дорофеев В. Ю.
©Издательство СПбГУЭФ, 2011
Предисловие.
Данное издание предназначено для студентов заочного факультета СПбГУЭФ изучающих курс математики.
Методические указания содержат примерные тестовые задания, предлагаемые на экзамене по математике студентам заочного отделения обучения и решения этих заданий.
Ознакомление с приведенным ниже материалом будет полезным при подготовке к экзамену по математике, как для студентов заочной, так и очно-заочной форм обучения.
Все задания распределены по трем частям.
Каждое задание, предлагаемое в первой части, требует простого ответа «да» или «нет» на каждый поставленный вопрос.
При выполнении заданий из второй части необходимо выбрать правильный ответ из нескольких предлагаемых вариантов.
В третьей части теста предлагается решить задачи и дать ответ в виде действительного числа.
За правильно выполненные задания начисляются баллы, которые затем суммируются.
Раздел первый
В этом разделе содержатся решения примерных тестовых заданий предлагаемых на экзамене по математике студентам первого курса заочного отделения и анализ решений этих заданий.
Часть I.
В этой части Вам предлагается 6 заданий, каждое из которых состоит из родственных друг другу вопросов. На каждый из вопросов Вы можете дать один из двух ответов: «Да» или «Нет» поставив отметку в соответствующей клетке таблицы в бланке ответов. Кроме того, Вы можете дать ответ «Не знаю», оставив обе, соответствующие вопросу клетки, пустыми. За каждое правильно выполненное задание начисляется один бал, в противном случае – ноль баллов.
Задание
I.
Пусть
существуют пределы
 ,
тогда выполняется свойство:
,
тогда выполняется свойство:
Решение. Если существуют пределы , то справедливы утверждения.
Предел постоянной величины равен самой постоянной величине:
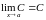 .
.
Предел суммы двух функций равен сумме пределов этих функций:
.
Постоянный коэффициент можно выносить за знак предела:
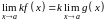
Предел произведения двух функций равен произведению пределов этих функций:
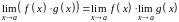
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
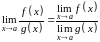 ,
если
,
если
 .
.
Вывод. Утверждение (1), (3) верны, а утверждения (2),(4) не верны.
Ответ: Да
Ответ: Нет
Ответ: Да
Ответ: Нет
Задание
II.
Функция
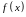 является бесконечно малой в точке
является бесконечно малой в точке
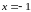 ,
если:
,
если:
Решение.
Функция
называется бесконечно малой при
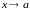 ,
где
,
где
 может быть числом или одной из величин
может быть числом или одной из величин
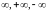 ,
если
,
если
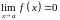 .
.
Бесконечно
малой функция может быть только в том
случае, если указать к какой величине
стремится аргумент
 .
При различных значениях
функция может быть бесконечно малой
или нет.
.
При различных значениях
функция может быть бесконечно малой
или нет.
Свойства бесконечно малых:
Сумма конечного числа бесконечно малых функций при тоже бесконечно малая функция при .
Произведение конечного числа бесконечно малых функций при тоже бесконечно малая функция при .
Произведение бесконечно малой функции на функцию, ограниченную вблизи точки
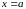 является бесконечно малой функцией
при
.
является бесконечно малой функцией
при
.Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть бесконечно малая функция.
Находим пределы
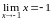 и
и
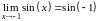 ,
следовательно
,
следовательно
 .
.
Вывод. Функция не является бесконечно малой в точке .
Ответ: Нет.
Отметим, что функция
 является бесконечно малой при
является бесконечно малой при
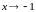 ,
а функция
,
а функция
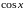 ограниченной, то
ограниченной, то
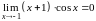 .
.
Вывод. Функция является бесконечно малой в точке .
Ответ: Да.
Вычислим предел
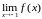 .
Поскольку
.
Поскольку
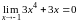 ,
то, следовательно, функция
действительно является бесконечно
малой в точке
.
,
то, следовательно, функция
действительно является бесконечно
малой в точке
.
Ответ: Да
Вычислим предел . Поскольку
 ,
то, следовательно, функция
не является бесконечно малой в точке
.
,
то, следовательно, функция
не является бесконечно малой в точке
.
Ответ: Нет
Задание
III.
Функция
является бесконечно большой в точке
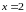 ,
если:
,
если:
Решение.
Отметим, что функция
является
бесконечно
большой при
,
если выполнено одно из соотношений
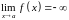 ,
или
,
или
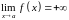 .
.
При
этом функция
,
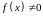 при
при
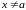 является бесконечно большой тогда и
только тогда, когда
является бесконечно большой тогда и
только тогда, когда
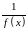 является бесконечно малой при
является бесконечно малой при
Находим предел:
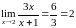
Вывод.
Функция
не является бесконечно большой при
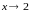 .
.
Ответ: Нет.
Находим предел:

Вывод.
Функция
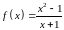 не является бесконечно большой при
.
не является бесконечно большой при
.
Ответ: Нет.
Находим предел функции . Имеем
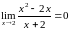
Вывод.
Поскольку функция
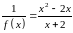 является
бесконечно малой при
,
то функция
является
бесконечно малой при
,
то функция
 является бесконечно большой при
.
является бесконечно большой при
.
Ответ: Да.
Находим предел
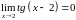 .
.
Вывод.
Функция
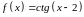 является бесконечно большой при
.
является бесконечно большой при
.
Ответ: Да.
Задание
IV.
Функция
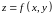 не имеет точек локального экстремума
если:
не имеет точек локального экстремума
если:
Решение. Сначала проверяем выполнение необходимого условия наличия точек локального, а за тем достаточное условие наличия точек экстремума.
Находим точки подозрительные на экстремум. Для этого находим первые частные производные и составляем систему уравнений:
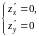 .
.
Имеем
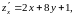
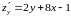
Следовательно, система для определения точек подозрительных на экстремум имеет вид
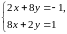
Определитель этой системы отличен от нуля, поэтому система имеет единственное решение – одну точку подозрительную на экстремум.
Находим вторые производные и проверяем достаточное условие наличия точек локального экстремума. Имеем

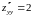 ,
,

Поэтому

Вывод. Функция не имеет точек локального экстремума.
Ответ: Да.
Находим первые частные производные
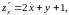
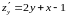
и составляем систему для нахождения точек подозрительных на экстремум:
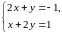
Определитель этой системы отличен от нуля, поэтому система имеет единственное решение – одну точку подозрительную на экстремум.
Находим вторые производные и проверяем достаточное условие наличия точек локального экстремума. Имеем
,
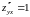
Поэтому
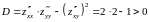
Вывод. Функция имеет точку локального экстремума.
Ответ: Нет.
Находим первые частные производные
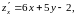
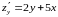
и составляем систему для нахождения точек подозрительных на экстремум:
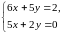
Определитель этой системы отличен от нуля, поэтому система имеет единственное решение – одну точку подозрительную на экстремум.
Находим вторые производные и проверяем достаточное условие наличия точек локального экстремума. Имеем
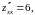 ,
,
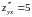
Поэтому

Вывод. Функция не имеет точек локального экстремума.
Ответ: Да.
Находим первые частные производные
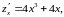
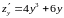
и составляем систему для нахождения точек подозрительных на экстремум:
.
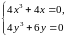
Эта
система имеет единственное решение.
Поэтому точка
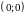 является единственной точкой подозрительной
на экстремум.
является единственной точкой подозрительной
на экстремум.
Находим вторые производные и проверяем достаточное условие наличия точек локального экстремума в точке . Имеем
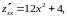
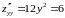 ,
,
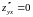
Поэтому

Вывод. Функция имеет точку локального экстремума.
Ответ: нет.
Задание V. Функция ограничена на плоскости, если:
Решение.
Функция
ограничена, если найдутся числа
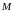 и
и
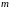 такие, что
такие, что
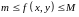 .
.
Утверждение неверно, так как, мы можем определить новую переменную
 и
и
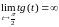 .
Поэтому не существует чисел
и
таких, что
.
.
Поэтому не существует чисел
и
таких, что
.
Ответ: Нет.
Утверждение верно, так как, мы можем определить новую переменную
 ,
а функция
,
а функция
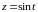 удовлетворяет неравенствам
удовлетворяет неравенствам
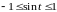 .
.
Ответ: Да.
Утверждение неверно, так как, мы можем определить новую переменную
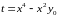 ,
(здесь
,
(здесь
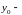 постоянная
величина) и функцию
постоянная
величина) и функцию
 ,
так что
,
так что
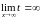 и
и
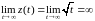 .
Поэтому функция
.
Поэтому функция
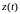 ,
при неограниченном увеличении
,
при неограниченном увеличении
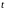 ,
будет больше любого наперед заданного
положительного числа
,
а это и означает, что функция
не ограничена.
,
будет больше любого наперед заданного
положительного числа
,
а это и означает, что функция
не ограничена.
Ответ: Нет.
Утверждение неверно, так как, мы можем определить новую функцию
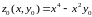 ,
при постоянном значении переменной
,
при постоянном значении переменной
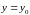 .
Поскольку
.
Поскольку
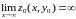 ,
функция
,
функция
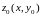 не ограничена, а это и означает, что
функция
тоже не ограничена.
не ограничена, а это и означает, что
функция
тоже не ограничена.
Ответ: Нет.
Задание VI. Неопределенный интеграл обладает свойством:
Решение.
Функция
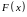 называется первообразной
функцией для данной функции
на данном промежутке, если на этом
промежутке
называется первообразной
функцией для данной функции
на данном промежутке, если на этом
промежутке
 .
.
Выражение,
 где
где
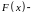 первообразная
функции
и
первообразная
функции
и
 произвольная
постоянная, называется неопределенным
интегралом
от функции
и обозначается символом
произвольная
постоянная, называется неопределенным
интегралом
от функции
и обозначается символом
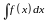 .
Таким образом, по определению,
.
Таким образом, по определению,
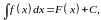 если
.
если
.
Неопределенный интеграл обладает свойствами:
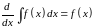 ,
следовательно,
.
,
следовательно,
. или
или
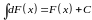
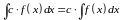
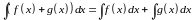
Рассматриваемое свойство соответствует свойству c), поэтому оно верно.
Ответ: Да.
Рассматриваемое свойство соответствует свойству a), поэтому оно верно.
Ответ: Да.
Пусть, например, функция
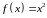 ,
а функция
,
а функция
 ,
тогда
,
тогда
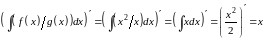 .
.
С другой стороны
 ,
,
Поэтому это свойство не верно.
Ответ: Нет.
Пусть, например, функция , а функция , тогда
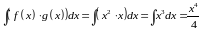 .
.
С другой стороны
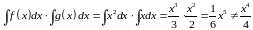 .
.
Поэтому это свойство не верно.
Ответ: Нет.
Задание
VII.
Если
и
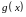 непрерывные функции, то определенный
интеграл обладает свойством:
непрерывные функции, то определенный
интеграл обладает свойством:
Решение.
Если
непрерывна на
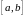 и
некоторая
первообразная функции
,
то (формула Ньютона-Лейбница)
и
некоторая
первообразная функции
,
то (формула Ньютона-Лейбница)
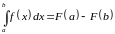 .
.
Определенный интеграл обладает свойствами:
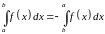
если функции
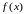 и
непрерывны на
,
то непрерывна их линейная комбинация
и
непрерывны на
,
то непрерывна их линейная комбинация
 и
и
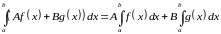
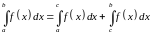
на отрезке найдется такая точка
 ,
что
,
что
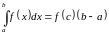 .
.
Рассматриваемое свойство соответствует свойству a), поэтому оно верно.
Ответ: Да.
Пусть, например, функция , а функция ,
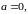
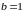 тогда
тогда
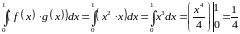 .
.
С другой стороны
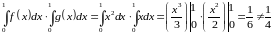 .
.
Поэтому это свойство не верно.
Ответ: Нет.
Рассматриваемое свойство соответствует свойству c), поэтому оно верно.
Ответ: Да.
Поскольку непрерывная функция, то используя формулу Ньютона-Лейбница, получим
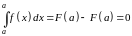 .
.
Но
при этом для произвольной непрерывной
функции
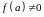 .
Поэтому это свойство не верно.
.
Поэтому это свойство не верно.
Ответ: Нет.