
Часть II.
В этой части Вам предлагается 14 заданий. На каждый из вопросов Вы можете дать один из четырех ответов «А», «Б», «В» или «Г», поставив отметку в соответствующей клетке бланка ответов. Кроме того, Вы можете дать ответ «Не знаю», оставив все четыре, соответствующие вопросу клетки, пустыми.
За каждое правильно выполненное задание начисляется один бал, в противном случае баллы не начисляются.
Задание
1. Укажите
соответствие, которое является функцией
 :
:
А.
|
Б.
|
В.
|
Г.
|
Решение.
Если
каждому значению аргумента
из множества
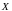 поставлено
в соответствие по определенному правилу
единственное
значение
поставлено
в соответствие по определенному правилу
единственное
значение
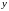 ,
то на этом множестве
задана функция.
,
то на этом множестве
задана функция.
В
таблице А
 и
и
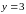 .
.
В
таблице Б
и
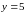 .
.
В
таблице В
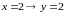 и
.
и
.
В
таблице Г
и
 .
.
Условию однозначности удовлетворяет только таблица Г.
Ответ: Г.
Задание
2. Предел
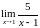 равен:
равен:
А.
|
Б.
|
В.
|
Г.
|
Решение.
Величина
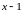 при
при
 является бесконечно малой. Обратная
величина
является бесконечно малой. Обратная
величина
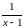 при
является бесконечно большой. Произведение
ограниченной на бесконечно большую
величину
при
является бесконечно большой. Произведение
ограниченной на бесконечно большую
величину
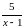 при
так
же
является
бесконечно большой величиной, поэтому
при
так
же
является
бесконечно большой величиной, поэтому
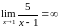 .
.
Ответ: Б.
Задание
3. Предел
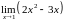 равен:
равен:
А.
|
Б.
|
В.
|
Г.
|
Решение.
Функция
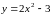 является непрерывной в точке
является непрерывной в точке
 .
Поэтому предел
равен
значению функции в точке
.
Поэтому предел
равен
значению функции в точке
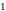 .
.
Именно
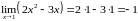 .
.
Ответ: Г.
Задание
4. Предел
 равен:
равен:
А.
|
Б. |
В. |
Г.
|
Решение.
Преобразуем
данный предел
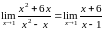 .
.
Величина
является
бесконечно большой при
,
а величина
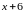 является ограниченной при
.
Поэтому
является ограниченной при
.
Поэтому
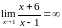 .
.
Ответ: В.
Задание
5. Предел
 равен:
равен:
А.
|
Б.
|
В. |
Г.
|
Решение. Преобразуем данный предел и определяем тип неопределенности
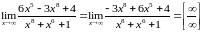 .
.
Полученная неопределённость раскрывается путём деления на старшую степень переменной.
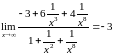 ,
,
поскольку
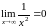 ,
,
 ,
,
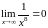 .
.
Ответ: Г.
Задание
6. Производная
функции
 равна:
равна:
А.
|
Б.
|
В.
|
Г.
|
Решение.
Функция
представляет собою произведение двух
функций
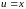 и
и
 .
Поэтому необходимо воспользоваться
формулой для производной произведения
двух функций
.
Поэтому необходимо воспользоваться
формулой для производной произведения
двух функций
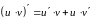 и
соответствующими табличными производными
и
соответствующими табличными производными
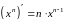 ,
,
 .
.
Следовательно
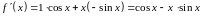
Ответ: В.
Задание
7. Производная
функции
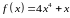 в точке
равна:
в точке
равна:
А.
|
Б.
|
В.
|
Г.
|
Решение.
Функция
представляет собою сумму двух функций
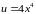 и
и
 .
Поэтому, при вычислении производной,
необходимо воспользоваться формулой
для производной суммы двух функций
.
Поэтому, при вычислении производной,
необходимо воспользоваться формулой
для производной суммы двух функций
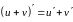 ,
свойством производной
,
свойством производной
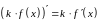 и соответствующей табличной производной
и соответствующей табличной производной
.
Следовательно
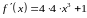 .
.
Поэтому
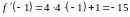
Ответ: А.
Задание
8. Дифференциал
функции
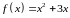 в точке
равен:
в точке
равен:
А.
|
Б. |
В.
|
Г.
|
Решение.
Дифференциалом функции
в
точке
называется главная часть её приращения,
равная произведению производной функции
на приращение аргумента, и обозначается
 или
или
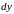 :
:

Поэтому
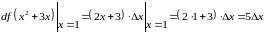
Ответ: А.
Задание
9. Уравнение
наклонной асимптоты к графику функции
 имеет вид:
имеет вид:
А.
|
Б.
|
В.
|
Г.
|
Решение.
Наклонная асимптота – это прямая вида
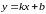 ,
где
,
где
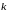 и
и
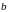 ,
при условии их существования определяются
пределами
,
при условии их существования определяются
пределами
 ,
,
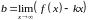 .
.
При этом функция не может иметь более двух наклонных асимптот и если хоть один из указанных пределов не существует, то наклонной асимптоты не существует.
Находим значение углового коэффициента :


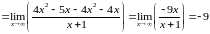
Ответ: А.
Задание
10. Для
функции
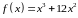 точка
точка
 есть точка перегиба. Тогда
равна:
есть точка перегиба. Тогда
равна:
А. |
Б.
|
В. |
Г. |
Решение.
Непрерывная на отрезке
 функция
называется выпуклой вверх на этом
отрезке, если для любых
функция
называется выпуклой вверх на этом
отрезке, если для любых
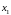 и
и
 из этого отрезка
из этого отрезка
 .
.
Аналогично определяется функция, выпуклая вниз.
Дважды
дифференцируемая на
функция
выпукла вверх, если для любого

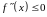 .
.
Дважды
дифференцируемая на
функция
выпукла вниз, если для любого
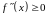 .
.
Пусть функция непрерывна в точке и имеет в этой точке конечную или бесконечную производную. Тогда точка называется точкой перегиба функции , если в этой точке изменяется направление ее выпуклости.
Необходимое
условие наличия точки перегиба.
Если
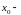 точка
перегиба функции
,
и функция
имеет вторую производную, непрерывную
в этой точке, то
точка
перегиба функции
,
и функция
имеет вторую производную, непрерывную
в этой точке, то
 .
.
Достаточное
условие наличия точки перегиба.
Пусть функция
непрерывна и имеет конечную или
бесконечную производную в точке
.
Если
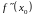 меняет знак при переходе через точку
,
то
точка
перегиба функции
.
меняет знак при переходе через точку
,
то
точка
перегиба функции
.
Для функции проверяем необходимое условие наличия точки перегиба.
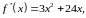


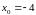 .
.
Проверяем достаточное условие наличия точки перегиба. Поскольку меняет знак при переходе через точку , то точка перегиба функции .
Ответ: Б.
Задание
11. Функция
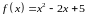 возрастает при:
возрастает при:
А.
|
Б.
|
В.
|
Г.
|
Решение.
Функция
называется возрастающей на множестве
( ),
если для любых
и
из этого множества и таких, что
),
если для любых
и
из этого множества и таких, что
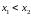 выполняется неравенство
выполняется неравенство
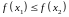 .
.
Для
того чтобы дифференцируемая функция
была возрастающей на множестве
,
необходимо и достаточно, чтобы её
производная
 была неотрицательной на множестве
.
была неотрицательной на множестве
.
Для функции проверяем необходимое и достаточное условие возрастания на множестве :
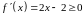
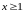 .
.
Следовательно,
на множестве
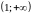 функция возрастает.
функция возрастает.
Ответ: Б.
Задание
12. Дифференциал
функции
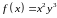 равен:
равен:
А.
|
Б.
|
В.
|
Г.
|
Решение.
Если функция
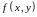 имеет непрерывные частные производные
имеет непрерывные частные производные
 и
и
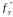 в точке
в точке
 ,
то она дифференцируема в этой точке и
её полный дифференциал
,
то она дифференцируема в этой точке и
её полный дифференциал
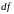 выражается формулой
выражается формулой
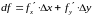
Найдем частные производные и
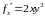 и
и
 .
.
Поэтому
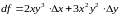 .
.
Ответ: Г.
Задание
13. Неопределенный
интеграл
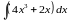 равен:
равен:
А.
|
Б.
|
В.
|
Г.
|
Решение.
Для произвольного
 справедлива формула табличного
интегрирования
справедлива формула табличного
интегрирования
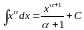
и для любых постоянных и
 .
.
Таким образом


Ответ: В.
Задание
14. Функция
 является производственной, если:
является производственной, если:
А.
|
Б.
|
В.
|
Г.
|
Решение. Производственная функция Кобба-Дугласа в теории производства в экономике определяет зависимость объема производства Q от создающих его затрат труда L и капитала K.
Функция впервые была предложена Кнутом Уикселлом. В 1928 году функция проверена на статистических данных Чарльзом Коббом и Полом Дугласом. Общий вид функции:
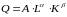 ,
,
где
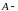 технологический коэффициент,
технологический коэффициент,
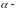 коэффициент
эластичности по труду, а
коэффициент
эластичности по труду, а
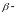 коэффициент эластичности по капиталу.
коэффициент эластичности по капиталу.
Если
сумма показателей степени
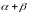 равна единице, то функция Кобба-Дугласа
является линейно однородной, то есть
она демонстрирует постоянную отдачу
при изменении масштабов производства.
равна единице, то функция Кобба-Дугласа
является линейно однородной, то есть
она демонстрирует постоянную отдачу
при изменении масштабов производства.
Если сумма показателей степени больше единицы, функция отражает возрастающую отдачу, а если она меньше единицы, - убывающую.
Коэффициенты эластичности выпуска продукции по труду и капиталу имеют положительные значения, так как интерпретируются следующим образом:
эластичность выпуска по труду - относительное изменение объема выпускаемой продукции за счет изменения вложений труда на 1 процент
эластичность выпуска по капиталу - относительное изменение объема выпускаемой продукции за счет изменения вложений капитала на 1 процент
Поскольку
приток дополнительного капитала и
привлечение дополнительной рабочей
силы способствуют увеличению производства,
коэффициенты обладают положительными
значениями. Таким образом, величины
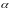 и
и
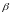 могут принимать только положительные
значения.
могут принимать только положительные
значения.
Кроме того, в силу закона убывающей предельной эффективности, вторые частные производные должны быть отрицательны. Таким образом величины и должны быть меньше единицы.
Ответ: Б.
