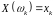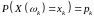3.2 Рівномірний дискретний розподіл

Дискретна випадкова величина називається рівномірно розподіленою, якщо вона набуває значень 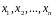з ймовірностями , .

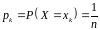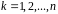Закон розподілу:

	1	2	3	...
				...

Функція розподілу:

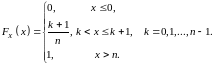
Числові характеристики:

, .

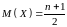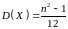3.3 Рівномірний неперервний розподіл

Неперервна випадкова величина називається рівномірно розподіленою на відрізку 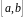, якщо її щільність ймовірності є сталою на і дорівнює 0 поза ним:

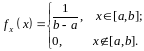
Графік функції 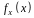має вид:

Функція розподілу:

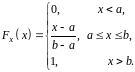
Числові характеристики:

, , .

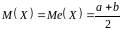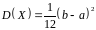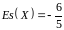3.4 Нормальний розподіл ймовірностей

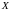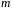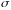Неперервна випадкова величина називається розподіленою за нормальним законом (законом Гаусса) з параметрами і , де 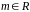, , 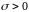якщо її щільність ймовірності має вигляд:

,

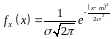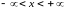
Позначається нормальний розподіл .

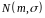Якщо випадкова величина розподілена за нормальним законом 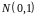з параметрами 0 і 1, то вона називається нормованою або стандартною нормальною випадковою величиною. Щільність стандартного нормального розподілу є функцією Гаусса:

.

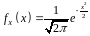Зауваження. Для значень функції Гаусса існують детальні таблиці.

Значення функції Гаусса можна обчислити

а) в Excel за формулою =НОРМРАСП(х; 0;1;ЛОЖЬ).

а) в Mathcad за формулою dnorm(x,0,1).

Функція розподілу:

.

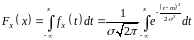Функція розподілу нормальної випадкової величини зв'язана з функцією Лапласа наступним співвідношенням:

.

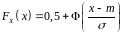Зауваження. Для значень функції розподілу нормальної випадкової величини існують детальні таблиці.

Значення функції цієї функції можна обчислити

а) в Excel за формулою =НОРМРАСП(х; 0;1;ИСТИНА)–0,5 або за формулою =НОРМСТРАСП(х)–0,5.

а) в Mathcad за формулою pnorm(x,0,1)–0,5.

Ймовірність того, що нормально розподілена випадкова величина набуває значень з деякого проміжку

.

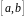
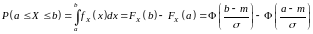Числові характеристики нормального розподілу збігаються з його параметрами:

, , .

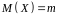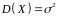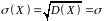3.5 Нормальне наближення

Локальна теорема Муавра-Лапласа

Дана теорема використовується для наближеного обчислення ймовірностей окремих значень биноміального розподілу. Вона стверджує, що рівномірно по всім значенням 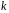має місце

,

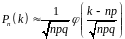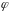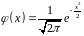де — щільність стандартного нормального розподілу, . (функція Гаусса.)

Інтегральна теорема Муавра-Лапласа

На практиці необхідність оцінки ймовірності окремих значень, яку дає локальна теорема Муавра-Лапласа, виникає нечасто. Набагато більш важливо оцінювати ймовірність подій, що включають в себе множину значень. Для цього використовується інтегральна теорема, яку можна сформулювати в наступному виді: При 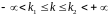, і

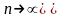
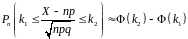
де 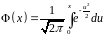— функція розподілу стандартного нормального закону (функція Лапласа).

3.6 Розподіли, пов’язані з нормальним

1) Розподіл 2 (хі-квадрат)

Якщо кожна з незалежних випадкових величин 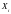, , 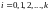характеризується стандартним нормальним законом розподілу ймовірностей 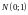, то кажуть, що випадкова величина 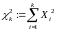має розподіл 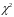із ступенями свободи із щільністю ймовірностей

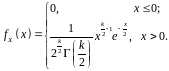
де 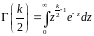– гамма-функція Ейлера.

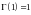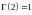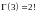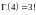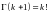( , , , , і взагалі, , – може бути нецілим числом: )

Функція розподілу:

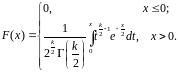
Розподіл використовують при оцінюванні дисперсії (за допомогою довірчого інтервалу), при перевірці гіпотез узгодження, однорідності, незалежності, передусім для якісних змінних, що набувають скінченне число значень, і в багатьох інших задачах статистичного аналізу даних.