Сложная или -рента

Простая рента предполагала одно начисление или один учёт на одном периоде ренты и одну выплату на этом периоде. Пусть теперь на одном периоде производится ...

Вспомним коэффициенты:

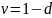– годовой коэффициент дисконтирования по годовой эффективной учётной ставке.

– годовой коэффициент наращения по годовой эффективной процентной ставке.

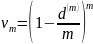– годовой коэффициент дисконтирования по годовой номинальной процентной ставке с m учётами в году.

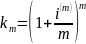– годовой коэффициент наращения по годовой номинальной процентной ставке с m начислениями в году.

Теперь представим, что у мы имеем 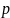выплат в год. Тогда:

– годовой коэффициент дисконтирования по годовой номинальной процентной ставке с m учётами в году на 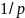части года.

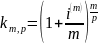– годовой коэффициент наращения по годовой номинальной процентной ставке с начислениями на части года.

На каждом частичном периоде выплата равна . Однако величины в этой выплате обычно учитывают в коэффициентах ренты. Тогда:

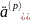
Очевидно, что коэффициент дисконтирования сложной ренты постнумерандо меньше коэффициента сложной ренты пренумерандо. Точнее, он равен:

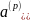
или:

По аналогии коэффициент наращения сложной ренты пренумерандо равен:

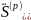
Коэффициент наращения сложной ренты постнумерандо равен:

или:

Итак, основные расчётные формулы для коэффициентов дисконтирования и наращения сложной ренты пренумерандо и постнумерандо имеют вид:

С помощью этих формул легко записать основные расчётные формулы для современных и наращенных стоимостей сложной ренты-пренумерандо и постнумерандо:

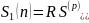
Рассмотрим несколько типичных случаев сложной ренты:

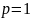1. , , т. е. и выплаты производятся один раз в год, и начисление – один раз в год. Таким образом, сложная рента превращается в простую, и все коэффициенты сложной ренты сводятся к соответствующим коэффициентам для простой ренты.

Аналогично и с остальными коэффициентами.

2. , , т. е. выплата производится один раз в год, а начислений или учётов – сколько угодно. Тогда подставив вместо p единицу, получим упрощённые формулы коэффициентов сложной ставки. Формулы станут менее громоздкими:

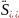
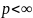3. , , т. е. начисление или учёт производится раз в году, а выплаты – постоянно, например, ежемесячно. Тогда подставим в формулы коэффициентов единицу вместо и снова сократим формулы. Буква “ ” исчезнет даже из обозначений: 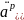и пр.

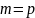4. , выплат производится столько же, сколько начислений или учётов. Этот случай похож на простую ренту, только вместо одного года надо брать -ю часть года. Но при этом ставка берётся уже не годовая. Вместо неё берутся 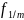для учёта и – для наращения.

5. , , т. е. начисление идёт непрерывно, а выплата – дискретна. Переходим к пределам по и используем второй замечательный предел. Получим:

18.02.2012 Практика

Задача 1.

Для создания страхового фонда ежегодно выделяется 4000 долларов. На аккумулируемые средства начисляются сложные проценты по ставке 6% годовых. Определить размер страхового фонда через 5 лет.

Общая модель – простая рента. Рента бывает пренумерандо и постнумерандо. Т. к. в задаче не уточняется, следует рассмотреть оба случая. Также ничего не сказано о ставке – процентная она или учётная. Следовательно, здесь также имеется 2 случая. Итого мы имеем 4 случая.

Решение:

1. Рента пренумерандо, процентная ставка.

Используем Формулу

2. Рента постнумерандо, процентная ставка.

Используем Формулу

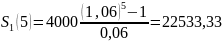
3. Рента пренумерандо, учётная ставка.

Переведём процентную ставку в учётную:

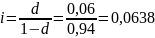
Используем Формулу

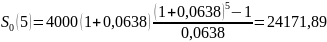
4. Рента постнумерандо, учётная ставка.

Переведём процентную ставку в учётную:

Используем Формулу

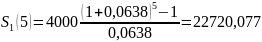
Задача 2.

Нефтяная компания ежемесячно выплачивает пенсию $500. Предполагая, что годовая номинальная процентная ставка равна 12%, подсчитать современную величину пенсионных выплат.

Решение:

Т. к. пенсия выплачивается в начале месяца, это пренумерандо.

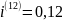– годовая номинальная процентная ставка

Нам нужно найти годовую учётную ставку. Переведём годовую номинальную процентную ставку в эффективную годовую процентную ставку, а её уже переведём в d.

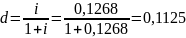
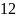Теперь находим , не забывая, что – это ежемесячная пенсия, а мы ищем годовую сумму. Т. е. умножаем на . Т. е.

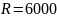
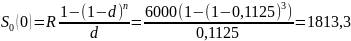
Задача 3:

Молодожёны имеют годовой доход в $16000. Ипотечный банк выдаёт сумму, которая должна погашаться 1/3-ей месячного дохода. Банк использует сложные проценты по месячной процентной ставке 1,2%. Долг погашается в течение 25 лет. Какова величина взятого кредита?

Решение:

Выплаты кредита производятся обычно в конце месяца, поэтому мы имеем ренту постнумерандо.

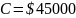
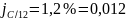
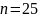
Найти: – ?

– величина взятого кредита

А номинальная сумма, которую молодожёны выплатят в итоге, получается: . Т. е. больше чем в 3 раза превышает сумму кредита. Довольно жёсткие условия, но молодожёны согласились.

Задача 4:

Накопительный фонд формируется по следующим схемам:

1. Годовая номинальная процентная ставка с ежеквартальным начислением процентов равна 12%, т. е.

2. 

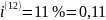
Сумма – 1 миллион.

Вопрос: какая схема выгоднее?

Решение: нужно сравнить коэффициенты наращения. Наиболее выгодной будет та схема, у которой он будет больше.

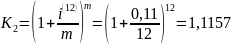
Вывод: вторая схема выгоднее.

Задача 5:

Семья планирует купить автомобиль за $20000. Банк выдаёт кредит на 5 лет при следующих условиях: начисление процентов ежеквартально, а выплата денег производится ежемесячно. Годовая номинальная процентная ставка составляет 16%, т. е. 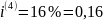. Найти величину ежемесячных выплат.

Решение:

Выплаты производятся в конце месяца, значит – рента постнумерандо

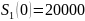
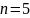
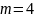– ежеквартальное начисление процентов

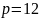– количество выплат в году (ежемесячно)

Вычислим :

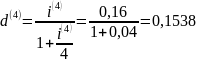
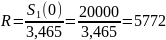
доллар выплачиваем ежемесячно за этот кредит.

Подсчитаем номинальную сумму, которую мы вернём за такой кредит: . Переплата большая.

25.02.2012 Лекция