Выбор наилучшей финансовой операции в условиях частичной определённости

В данной ситуации применяются следующие правила:

1. правило Байеса максимизации среднего ожидаемого дохода

2. правило Байеса минимизации среднего ожидаемого риска.

Предположим, что из статистики или других источников известны вероятности исходов 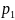, , 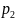..., . 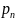Здесь 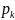– это вероятность -го исхода, . Если в матрице доходов или в матрице рисков предусмотреть все возможные исходы, то сумма соответствующих вероятности должны ровняться :

Правило Байеса максимизации среднего ожидаемого дохода.

Определим средний ожидаемый доход финансовой операции как математическое ожидание случайной величины – вектора доходов по этой операции при всевозможных исходах. Этой случайной величине соответствует -тая строка матрицы доходов .

Закон распределения этой дискретной случайной величины:

			…
			…

Математическое ожидание этой случайной величины выражается в виде скалярного произведения её значений на соответствующие вероятности:

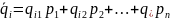
После того, как найдены средние ожидаемые доходы, по каждой финансовой операции набирается наибольшая величина:

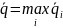
Соответствующая финансовая операция объявляется наилучшей.

Правило Байеса максимизации среднего ожидаемого риска.

Вместо матрицы доходов рассматривается матрица рисков . По аналогии, каждую строку можно рассматривать как случайную величину, имеющую следующий закон распределения:

			…
			…

Определяем средний ожидаемый риск как математическое ожидание случайной величины – вектора рисков по этой операции при всевозможных исходах. Этой случайной величине соответствует -тая строка матриц . Математическое ожидание этой случайной величины выражается в виде скалярного произведения значений этой случайной величины на соответствующие вероятности:

После подсчёта средних ожидаемых рисков по каждой финансовой операции выбирается наименьшее значение:

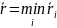
Соответствующая операция объявляется наилучшей.

С учётом частичной неопределённости дорешаем наш Пример 1:

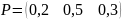
Матрица – это матрица вероятностей появления соответствующего исхода, т. е. , 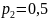и . Эти вероятности мы получили из статистики или какого-то другого источника.

Найдём 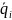по формуле и выберем среди найденных наибольший:

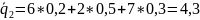
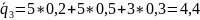
Наибольшим будет . Следовательно, по правилу Байеса максимизации ожидаемого дохода, наилучшей финансовой операцией становится .

Применим правило минимизации ожидаемых рисков – найдём по формуле и выберем среди найденных наименьший:

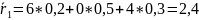
Наименьшим риском становится , а значит, и по правилу минимизации ожидаемых рисков первая финансовая операция считается наилучшей. Т. е. получили ответ без противоречий. Если бы возникли противоречия, то следовало бы составить оптимальное множество Парето.

Вспомним формулы вычисления дисперсии:

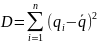
Среднее квадратичное отклонение равно квадратному корню из дисперсии и в финансовых расчётах называется средним ожидаемым риском: .

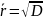24.03.2012 Контрольная работа (по предыдущей лекции) в начале пары + новая лекция