§ 7. Шкала роста бесконечно больших при элементарных функций

Рассмотрим множество степенных функций с положительным показателем степени и дополним это множество логарифмической и показательной функциями:

.

Все эти функции при принимают бесконечно большие значения, но каждая из них имеет свой порядок роста (свою «скорость» роста). Порядок расположения функций во множестве соответствует их порядку роста при . Чем правее расположена функция в указанном множестве, тем она имеет более высокий порядок роста.

Таким образом, начиная с логарифмической функции и кончая показательной функцией, мы имеем некую шкалу роста функций -  направленное множество функций, направленность которого связана с порядком роста функций при .

Несмотря на то, что все функции из множества при принимают сколь угодно большие значения, любая функция, расположенная левее по шкале роста, по сравнению с функцией, стоящей справа, является бесконечно малой функцией.

Порядок расположения функций по шкале роста связан и продиктован справедливостью следующих предельных соотношений:

.

.

,   

Здесь число является ближайшим целым числом к числу . При вычислении последнего предела, ( ) раз применялось правило Лопиталя .

Итак, среди всех бесконечно больших функций рассматриваемого множества «самой медленной» при функцией является логарифмическая функция , а «самой быстрой» - показательная функция .

Анализируя поведение функций при удобно применять представленную шкалу роста элементарных функций, лишний раз не прибегая к явному использованию правила Лопиталя. Рассмотрим несколько примеров.

Пр. 1 Вычислим предел функции .

Сравнивая две функции под корнем, и учитывая их расположение по шкале роста, первой из них можно пренебречь по сравнению со второй. Далее сравнивая оставленную функцию с логарифмической функцией числителя, с учетом их расположения по шкале роста, пренебрегаем логарифмической функцией

о о

.

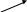
Пр.2 Вычислим предел функции .

Освободимся от отрицательной степени у второго слагаемого числителя и представим степенную функцию третьего слагаемого числителя в виде показательной функции с помощью основного логарифмического тождества. В знаменателе пренебрегаем единицей по сравнению с бесконечно большой функцией. Рассматриваемый предел запишется в виде

о

.

Здесь при вычислении предела отношения логарифмической и показательной функций было учтено, что порядок роста показательной функции выше чем логарифмической в соответствии со шкалой роста функций, и поэтому значение предела определялось главным образом поведением знаменателя дроби, который, стремясь к бесконечности, привел к нулевому предельному значению указанного отношения.

Возможность пренебречь слагаемым по сравнению с продиктована тем, что при логарифмическая функция, сама стремится к бесконечности и может рассматриваться как некоторая переменная, например, , тогда квадрат логарифма становится равным и в соответствии со шкалой роста бесконечно больших функций, величина оказывается бесконечно малой по сравнению с и ею возможно пренебречь.

Замечание: Постоянные множители, которые можно добавить к функциям из рассматриваемого множества бесконечно больших функций в шкале роста, не меняют место положения самих функций в шкале роста и поэтому множитель 2 перед логарифмом не играет никакой роли при сравнении указанных функций.

Вычисление последнего предела произведено в результате сравнения порядков роста функций и в соответствии со шкалой роста. При этом значение предела определяется главным образом ростом числителя дроби, а не знаменателя.

Пр. 3 Вычислим предел функции

Ввиду того, что основанием степенной и логарифмической функций здесь не является число , да и аргументами этих функций не является , непосредственное применение шкалы роста для вычисления предела оказывается невозможным. Однако, поскольку основания степенной и логарифмической функций являются числа, большие единицы, можно предположить, что для рассматриваемых функций шкала роста также может быть использована, тогда, пренебрегая степенной и логарифмическими функциями, оставляем только показательную. В этом случае искомым пределом должно являться выражение . Покажем, что это действительно так:

о о о

.

Здесь пренебрежение степенной и логарифмической функциями оказалось возможным в виду существования предельных соотношений:

.

.