Д. Н. КАЧЕВСКИЙ
ГРАФИКИ ФУНКЦИЙ
Учебное пособие по высшей математике
Чебоксары «ДНК» 2008
К 30
УДК 517
Качевский Дмитрий Николаевич
К 30 Графики функций. Учебное пособие по высшей математике. – Чебоксары: ДНК, 2008, 25 с., ил.
В учебном пособии посвящено экспресс методу построения графиков функций на основе вычисления пределов функций на границах области определения.
Помимо большого количества примеров схематического построения графиков функций в пособие включены типовые задания для самостоятельной работы. Для освоения представленного материала предполагается наличие навыков вычисления пределов и дифференцирования. Пособие предназначено для студентов вузов всех форм обучения, для школьников с углубленным изучением математики, а также для специалистов широкого профиля, занимающихся анализом графических закономерностей.
© Чебоксары, «ДНК», 2008.
Графики функций
Исследование и построение графиков функций часто представляет собой задачу весьма сложную, с громоздкими вычислениями. В то же время, оказывается возможным и быстрое, достаточно простое схематическое построение графиков функций с помощью вычисления пределов функции на границах ее области определения. Последнему методу и посвящено данное учебное пособие
§ 1. Общая схема исследования и построения графика функции.
Нахождение области определения функции (области допустимых значения аргумента-ОДЗ).
Сужение (уменьшение) рассматриваемой области определения для четных (нечетных), а также для периодических функций.
Поведение функции на границах области определения - находится с помощью вычисления соответствующих пределов.
Нанесение значений вычисленных пределов на координатную плоскость. Предварительный рисунок графика функций.
Проверка существования дифференцируемых и недифференцируемых локальных экстремумов. (Нахождение критических точек – точек обращения в нуль производной; точек разрыва производной, обращения ее в бесконечность).
Уточнение предполагаемого графика функции по найденным локальным экстремумам и точкам разрыва производной. Нанесение на график функции характерных точек функции и точек пересечения с осями координат.
Дальнейшее уточнение графика функции, если это требуется.
( Нахождение наклонных асимптот, точек перегиба и др.).
Окончательное построение графика функции с продолжением его на всю область определения (если было сужение области, связанное с четностью, периодичностью функции).
Приведем
здесь формулы для нахождения параметров
наклонных асимптот функции
:
Для наклонной асимптоты
параметры могут быть найдены по формулам:
.
§ 2. Примеры построения графиков функций
Пр.1
Построим
график функции
.
ОДЗ:
.
С
учетом нечетности функции
произведем сужение области определения,
отбрасывая из рассмотрения область
отрицательных значений аргумента:
ОДЗ:
.
Выясним поведение функции на границах ОДЗ:
;
.
Нанесем на координатную плоскость результаты вычисления пределов (Рис. 1):
y
y
Р
ис.1 
Рис.
2
0
1
x
0 1 x
Теперь можно нарисовать предположительный вид графика функции (Рис. 2).
Убедимся, в справедливости нашего предположения. Проверим, что на графике отсутствуют локальные экстремумы.
Найдем первую производную функции, попытаемся приравнять ее нулю:
.
Поскольку в числителе имеем отрицательное число, производная в нуль не обращается. Следовательно, критических точек на графике функции нет, как нет и дифференцируемых экстремумом.
Найдем,
в каких точках производная не существует
или обращается в бесконечность.
Приравнивая знаменатель производной
нулю, получаем значение такой точки:
.
Однако из Рис.
2 мы уже
знали, что при
производная обращается в бесконечность
(слева от
это
,
справа
).
Таким образом, на Рис.
2 график
изображен правильно.
Сделаем
одно уточнение. Найдем под каким углом
пересекает начало координат график
функции. Для этого подставим абсциссу
начала координат
в найденную производную:
.
Таким
образом, пересечение графика функции
начала координат осуществляется под
углом
,
примерно так, как мы и нарисовали.
С учетом нечетности функции, продолжим график функции на всю числовую ось, и окончательно получим искомый график (Рис. 3).
y Рис.
4
-1 0 1 x
Пр.2
Построим
график функции.
.
ОДЗ:
.
Исследуем поведение функции на границах области определения:
о
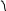
о 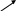о
;
;
;
;
;
;
о
.
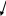
о о
Нанесем результаты вычисления пределов на координатную плоскость (Рис. 5):
y
Рис. 5
-1
0 1 2 3
x
Предположительный график функции теперь может быть изображен на Рис.6:
y
Рис.
6
-1
0 3 x
2
Теперь
остается убедиться в существовании
одного экстремума (одного максимума с
координатами (
))
изображенного на Рис.6.
Найдем
координаты
.
Для этого вычислим производную функции:
Приравнивая производную нулю, находим что единственным
действительным
корнем числителя является значение
,
где 
.
Соответствующее
значения функции
.
Таким
образом, предположительный график
функции, изображенный на Рис.
6 , соответствует
действительности. Точка пересечения
графика с осью абсцисс:
.
( В этой точке функция, обращается в
ноль.)
Пр.3
Построим
график функции
.
ОДЗ:
.
Учитывая,
что функция четная (функция не «чувствует»
изменения знака
,
т. е.
,
произведем сужение области определения
функции, ограничиваясь рассмотрением
только положительных
:
ОДЗ:
.
Выясним поведение функции на границах области определения:
.
Добавление (-0) показывает, что предельное значение 1 достигается функцией, которая при конечных принимает значения, меньшие единицы.
Наносим значения вычисленных пределов на координатную плоскость (Рис. 7):
y
y
1 1
Р
ис.
7 Рис. 8
X x
Предполагаемый график функции изображен на Рис. 8. График функции при всех значениях располагается ниже прямой линии . Сама прямая является горизонтальной асимптотой. График будет иметь такой вид, если функция во внутренних точках ОДЗ не имеет экстремумов. Проверим это. Найдем производную функции:
.
Ввиду того, что числитель дроби не обращается в ноль, производная функции не равна нулю, следовательно на графике отсутствуют дифференцируемые локальные экстремумы. Таким образом, предполагаемый график функции (Рис. 8) действительно является графиком функции.
Для
уточнения графика найдем точки разрыва
производной. Таким точкам соответствует
случай обращения производной в
бесконечность. Для этого знаменатель
у производной должен обратиться в ноль.
Единственная возможность для этого -
обращение в ноль
.
Таким образом, при
производная функции обращается в
бесконечность и график функции пересекает
начало координат вертикально. Учитывая
последнее обстоятельство, и продолжая
график функции на всю область определения,
с учетом четности функции окончательно
получаем искомый график (Рис.
9).
y
1
x
Рис. 9
Пр.
4 Построим
график функции
.
Рассматриваемая
функция является периодической с
периодом
.
Сразу произведем сужение области
определения функции и будем изучать
поведение функции лишь на множестве
.
О
ДЗ:
.
Найдем поведение функции на границах области определения:
.
.
.
.
Здесь для вычисления значений тригонометрических и логарифмической функций были использованы их графики:
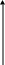
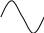
o
x 0
x 0
1 x
Рис. 10
Нанесем вычисленные значения пределов на координатную плоскость (Рис.11):
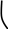y
y
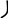
0
x
0
x
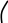
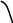
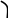
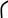
Рис. 11 Рис. 12
Предполагаемый график функции изобразим на Рис. 12. Убедимся, что в соответствии с предполагаемым видом графика, функция не имеет локальных дифференцируемых экстремумов. Для этого найдем критические точки, приравняв производную функции нулю:
.
Покажем
сначала, что на отрезке от 0 до
существует только одна критическая
точка
.
Обозначая
,
(учитываем, что на этом интервале
,
а, следовательно, и
)
приравняем числитель предыдущего
уравнения нулю, освободившись от квадрата
под знаком логарифма. Заменив
,
имеем:
.
Полученное уравнение решим графически (см. Рис. 13):
y
1
t t
Рис. 13
-1
Покажем
теперь, что и на отрезке от
до
также существует только одна критическая
точка
.
Приравняв числитель производной
нулю, предварительно заменяя
,
(на рассматриваемом интервале
,
следовательно
),
имеем:
.
Решая,
как и в первом случае, то же самое
уравнение, графически (см. Рис. 13),
убеждаемся в существовании на
рассматриваемом интервале только одной
критической точки
,
а, следовательно,
,
откуда
.
Таким
образом, из предполагаемого графика
функции на Рис. 12 убеждаемся, что
найденные критически точки
не могут являться локальными экстремумами,
т. к. в противном случае для каждой из
них должны бы существовать еще по одной
критической точке, чтобы график функции
имел, например, вид, изображенный на
Рис.14.
y
x Рис. 14
0
Ввиду того, что найденные критические точки не являются точками экстремума, они представляют собой точки перегиба с горизонтальными асимптотами.
Проверим, что у заданной функции отсутствуют и недифференцируемые экстремумы. Для этого убедимся, что производная нигде во внутренних точках области определения не имеет разрыва.
Из
вида производной следует, что единственными
точками, в которых производная не
существует (обращается в бесконечность),
являются точки, соответствующие решению
уравнения
,
(т. к.
располагается в знаменателе
,
а также является аргументом логарифма,
а
).
Однако указанные точки (
) уже
были исключены из рассматриваемой
области определения и график предполагаемой
функции (Рис. 12) уже отражал тот факт,
что в указанных точках производная
функции обращается в бесконечность.
Таким
образом, отмечая на графике найденные
точки перегиба (с горизонтальными
асимптотами), соответствующие значениям
и
и продолжая график Рис.12
на всю числовую ось, с учетом периодичности
функции, получаем искомый график функции
:
Рис. 16
y
x
Пр.
5 Построим
функцию
.
ОДЗ:
>
> 0.
Решаем неравенство методом интервалов:
(+)
(+)
-1/2 (-) -1/3 
.
Исследуем поведение функции на границах области определения:
.
.
.
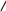
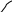
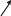o
.
о
Найденные значения пределов наносим жирными штрихами на
y
Рис.
17
x
координатную плоскость, а предполагаемый график функции рисуем тонкой линией, (Рис. 17). Конец стрелки на графике означает исключение соответствующей точки из графика.
Убедимся в правильности предположения о виде графика функции. Найдем точки дифференцируемых локальных экстремумов. Для этого найдем производную функции и приравняем ее нулю.
.
Производная
может равняться нулю только за счет
обращения в ноль квадратной скобки.
Приравнивая ее нулю, решая уравнение
графически, находим два корня уравнения:
=0 . Соответствующие
значения функции при этом находятся
как:
.
Теперь
уточним угол, под которым график
«пересекает» ось абсцисс в точке
.
Для этого вычислим предел:
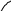
о
.
При вычислении предела пренебрегли первым слагаемым в квадратной скобке поскольку рост логарифмической функции происходит значительно медленнее роста любой степенной функции. В нашем случае имеем:
.
Таким
образом, график функции «пересекает»
ось абсцисс в точке
вертикально. Внесем все уточнения в
Рис. 17 и изобразим на
Рис. 18
окончательно график функции
:
y
Рис. 18
2
1
-1 …-0,84 -0,5 -1/3 0 x
Пр.
6 Построим
функцию
.
О
ДЗ:
.
Исследуем поведение на границах ОДЗ:
. 
.
. 
.
.
.
Результаты вычисления пределов нанесем на координатную плоскость жирными штрихами, а предполагаемый график функции – тонкой линией (см. Рис.19):
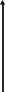
y
Рис.
19
-3 0
x
Убедимся в отсутствии дифференцируемых локальных экстремумов, для чего найдем производную функции и попытаемся приравнять ее нулю:
.
Ввиду
того, что дискриминант числителя
отрицателен, производная в ноль не
обращается, это означает, что у функции
нет дифференцируемых локальных
экстремумов, а также отсутствуют точки
на графике, в которых касательная
горизонтальна. Производная функции не
существует в точках
,
которые исключены из области определения
функции, т. е. у функции отсутствуют и
недифференцируемые локальные экстремумы.
Таким образом график функции, изображенный
на Рис. 19 соответствует действительности.
Уточним его, проверив наличие наклонных
асимптот:
Предполагаем
наличие асимптоты с уравнение.
у функции при
.
Если таковая имеется, найдем ее параметры:
.
.
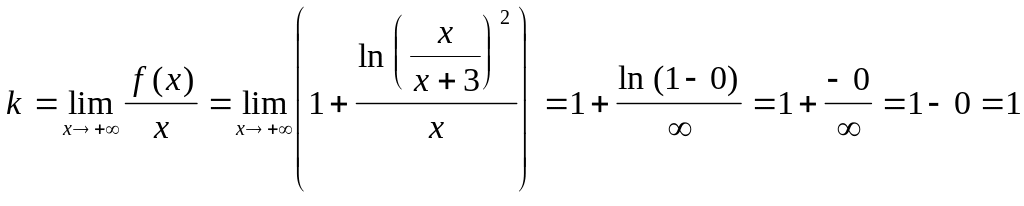Таким
образом, при
действительно имеется наклонная
асимптота с уравнением
,
причем знак минус перед нулем в правой
части предыдущего равенства означает,
что функция
т. е. график функции располагается при
ниже самой асимптоты .
Аналогичным
образом найдем наклонную асимптоту
при
.
Полагая, что уравнение ее опять имеет вид , найдем параметры асимптоты:
.
.
Здесь были использованы формулы для функций, эквивалентных в нуле (Гл. I, § 4).
Знак
(+) перед нулем в последнем выражении
можно трактовать так, что при
график функции
располагается выше асимптоты
поскольку
.
С помощью найденных асимптот уточним Рис. 19, и нарисуем искомый график функции, см. Рис. 20:
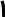y
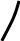
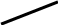
Рис. 20
-3 0 х
Пр.
7 Построим
график функции
.
ОДЗ:
.
Поведение функции на границах ОДЗ:
.
.
Вычисленные пределы обозначим жирными штрихами на координатной плоскости, а предполагаемый график функции рисуем тонкой линией (Рис. 21).
y
Рис.
21
Координаты локального максимума
(1, 
).
0 x
Найдем точку предполагаемого дифференцируемого локального максимума:
.
Приравнивая
производную нулю, находим критическую
точку
,
соответствующую локальному максимуму
.
Поскольку
график проходит через начало координат,
найдем угол, под которым пересекается
ось абсцисс:
.
Из вида производной заключаем, что недифференцируемых локальных экстремумов у функции нет, т. к. производная существует и принимает конечные значения на всей области определения функции.
Проверим наличие при наклонной асимптоты :
.
Поскольку параметр предполагаемой асимптоты не является конечной величиной , наклонной асимптоты не существует. Функция действительно изображена на Рис. 21.
Пр.
8 Построим
график функции
.
(плотность логнормального распределения)
ОДЗ:
> 0 
.
Выясним поведение функции на границах области определения:
о о
.
.
Нанесем результаты вычислений жирными штрихами на координатную плоскость, а предполагаемый график функции тонкой линией (Рис. 22).
y
x Рис.
22
Найдем предполагаемый дифференцируемый локальный максимум функции.
.
Приравнивая
производную нулю, получаем абсциссу
локального максимума:
.
Для соответствующей ординаты получаем
значение 
0,005.
Недифференцируемых локальных экстремумов функция не имеет т. к. производная существует в каждой точке ОДЗ (не имеет разрывов и не обращается в бесконечность).
Найдем угол, под которым график функции “пересекает” ось абсцисс в начале координат:
о о
о
.
Таким образом, график функции приближается справа к началу координат горизонтально (угол между графиком и осью абсцисс равен нулю ).
Сделаем более точный рисунок графика функции ( Рис. 23 ):
y
0,005
Рис.
23
о
55
х
Здесь абсциссы двух точек перегиба и могут быть найдены из равенства нулю второй производной функции .
Пр.
9 Построим
график функции
.
ОДЗ:
.
Для
удобства дальнейших вычислений сначала
построим график функции
,
(«перевернутый» график тангенса), (Рис.
24).
y
0 x Рис. 24
Найдем поведение графика функции на границах области определения:
о
.
.
.
.
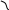
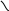
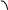
Здесь
добавки
к значениям
взяты из графика
.
Действительно, значение
достигается арктангенсом со стороны
меньших углов, а значение
достигается арктангенсом со стороны
больших углов. А при вычислении пределов
при
воспользовались разложением в ряд
Тейлора арктангенса в соответствии с
формулой:
.
Замечая,
что график функции проходит через начало
координат (т. к.
),
нанесем жирными штрихами значения
вычисленных пределов на координатную
плоскость, а предполагаемый график
функции тонкой линией (см. Рис. 25)
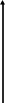y
0 3
х Рис. 25
Теперь остается проверить, что, действительно, как следует из Рис. 25, исследуемая функция не имеет дифференцируемых локальных экстремумов.
.
Поскольку производная в ОДЗ в ноль не обращается, дифференцируемые локальные экстремумы отсутствуют.
Интересной
особенностью графика функции является
то, что в исключенной из ОДЗ
точке
функция не обращается в бесконечность,
а имеет разрыв первого рода (конечный
скачок). Для уточнения графика интересно
выяснить под каким углом график функции
“пересекает” вертикальную прямую
.
Как видно из вычисленного значения предела этот угол не равен ни нулю, ни 90°, но слева и справа от вертикали наклоны касательных к разным веткам графика одинаковые. На Рис. Этот факт отмечен.
Пр.
10 Построим
график функции
.
Обратим внимание на то, каким образом меняется график функции, если функция взята по модулю (Рис. 26):
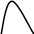
A B A B
x x
Рис. 26
График функции, взятой по модулю, отличается от графика самой функции тем, что отрицательные значения функции становятся положительными , не меняясь при этом по модулю (участок кривой между точками А и В симметрично отображается на верхнюю полуплоскость). Положительные же значения функции при этом не меняются.
Таким образом, в точках, пересечения графика функции с осью абсцисс, происходит резкое изменение направления касательной к графику, т. е. производная функции при этом претерпевает разрыв, следовательно, в этих точках производная функции не существует (существует производная слева и производная справа, не совпадающие друг с другом).
Найдем
область определения заданной функции
.
О
ДЗ:
.
Поведение
функции на границах области определения:
.
.
.
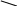
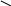Нанесем
жирными штрихами значения вычисленных
пределов на координатную плоскость. С
учетом характерных точек, через которые
проходит график,
, 
,
рисуем тонкой линией и линией пунктирной
два возможных предполагаемых графика
функции, (Рис. 27):
y
y
-5
-4 x - - 2 - 1
.. 0 …. x
Рис.
27
С помощью первой производной удостоверимся в существовании локального максимума, и найдем его, а также выясним, имеются ли точки разрыва производной.
Всю
область определения разобьем на участки
точками, в которых
,
и для каждого участка, освободившись
от модулей , запишем заданную функцию
в виде:
.
Учитывая,
что на участке
функция
положительна,
один из предполагаемых графиков функции,
а именно, график, изображенный пунктиром,
не может являться графиком рассматриваемой
функции.
Найдем производную функции:
.
Если
приравнивать производную нулю для
каждой из трех рассматриваемых областей,
и решать соответствующие уравнения
графически, то можно видеть, что только
в области
существует один действительный корень
уравнения
,
равный
с соответствующим значением функции
.
Таким образом, в соответствии с Рис. 27
найден единственный дифференцируемый
максимум функции, имеющий координаты
(-3,22 ; 1,42 ).
С
помощью найденной функции
проверим
существование точек разрыва производной.
Разрыв производной возможен лишь в
точках, где производная обращается в
бесконечность ( из внешнего вида
видно, что это возможно только при
)
и в точках, разделяющих три участка
графика функции (
).
.
.
.
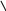
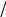
о
.
Таким
образом, мы убеждаемся, что в точке
при
производная имеет разрыв первого рода,
т. е. график функции имеет острый излом,
(см. Рис. 28 ), а в точке
имеется вертикальная асимптота, как и
следовало из Рис. 27.
y
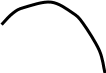
1,42 y=|x+5| ·ln | x+1 |
-5 4 -3 -2
-1 0 x
Рис. 28