Д. Н. КАЧЕВСКИЙ
ПРЕДЕЛЫ
МЕТОДЫ ВЫЧИСЛЕНИЯ
Учебное пособие по высшей математике
Издание второе
Чебоксары «ДНК» 2008
К 30
УДК 517
Качевский Дмитрий Николаевич
К 30 Пределы. Методы вычисления. Учебное пособие по высшей математике. – Чебоксары: ДНК, 2008, 45 с., ил.
Излагаются правила и методы вычисления пределов функций; рассматриваются все виды неопределенности; приводится большое количество примеров вычисления пределов. Для самостоятельной работы студентов пособие снабжено типовыми заданиями по вычислению пределов. Пособие предназначено для студентов дневной формы обучения экономических и технических специальностей.
© Чебоксары, «ДНК», 2008.
Предисловие ко второму изданию
Необходимость издания учебного пособия по практическим методам вычисления пределов продиктовано неудовлетворительным по нашему мнению изложением указанных разделов математического анализа в учебной литературе, где часто в силу формализованного подхода к вычислению пределов, у студентов складывается лишь поверхностное представление об этом процессе, и вычисление предела ими проводится нередко даже без анализа вида имеющейся неопределенности.
Помимо основных методов вычисления пределов в пособие включен сборник заданий для самостоятельной работы студентов, а также примеры выполнения этих заданий.
Автор
Введение
Предлагаемое учебное пособие представляет собой достаточно подробное изложение правил и методов вычисления пределов функций с примерами и сборником заданий для самостоятельной работы студентов. Пособие предназначено в основном для студентов дневного отделения экономических и технических специальностей, однако может быть использованы и студентами всех форм обучения.
§1. Бесконечность и ноль. Правила обращения
Дополним
множество действительных чисел двумя
“несобственными числами”:
и
(плюс бесконечность и минус бесконечность,
знак (+) можно опускать), которые определим
с помощью свойств:
1°
,
,
(
действительное
число).
2°
,
.
3°
для
> 0;
для
< 0.
4° 
.
5° 
.
(Величина
(
)
понимается как сколь угодно малая
положительная или отрицательная
величина).
6°
(
< 
).
7° 
(
> 
).
8° 
(
<
).
9° Графическое
представление бесконечности на оси
:
Рис. 1
0
Приведенные свойства дают возможность трактовать бесконечность как сколь угодно большое положительное или отрицательное число, обратное положительному или отрицательному нулю. О бесконечности как предельном значении числовой последовательности см. § 2.
§2. Числовая последовательность. Предел числовой последовательности
Определение:
Числовой последовательностью
будем называть множество чисел:
, каждое из которых имеет свой порядковый
номер, по которому однозначно определяется
по определенному правилу соответствующий
элемент последовательности (член
последовательности). Если задан
ый
член последовательности
,
то по нему можно восстановить и всю
последовательность. Например,
, тогда имеем числовую последовательность
Если
с возрастанием номера
члены последовательности приближаются
сколь угодно близко к некоторому числу
, то это число будем называется пределом
числовой последовательности ,
при этом числовая последовательность
называется сходящейся
к числу
.
Применяются обозначения:
,
или 
.
Одно и то же число может быть пределом многих числовых последовательностей. Например,
.
Но, если последовательность имеет предел, то этот предел единственен и не зависит от способа его вычисления. Например, вычисляя предел
числовой
последовательности
с четными
,
получаем значение предела , равное нулю,
с нечетными – значение предела либо
+1, либо –1 в зависимости о выбранных
значений нечетных чисел. Таким образом
предела данной числовой последовательности
не существует. Это можно установить,
также если восстановить все члены
последовательности
.
Видно, что с ростом члены последовательности не приближаются сколь угодно близко ни к какому числу.
Теперь дадим строгое определение предела последовательности:
Определение:
Число
называется пределом числовой
последовательности
,
если для любого положительного числа
найдется такой номер
,
что при всех
члены последовательности удовлетворяют
неравенству
.
Будем
называть
числовую
последовательность
бесконечно
большой,
если с ростом
члены последовательности по модулю
могут превысить сколь угодно большое
положительное число. В этом случае можно
записать:
(если начиная
с некоторого номера все члены
последовательности положительны)
;или
(если начиная с некоторого номера все
члены последовательности отрицательны).
Приведем примеры бесконечно больших последовательностей:
, 
.
Таким образом, среди бесконечно больших последовательностей имеются последовательности с пределом, равным бесконечности, пределом, равный минус бесконечности, а также последовательности, не имеющие предела (например, в силу его неединственности, так как для четных и нечетных знак бесконечности разный).
Пример 1. Найти предел числовой последовательности
.
Решение
примера
:
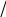
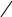
0
0
.
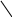
0
Стрелочка с нулем здесь означает, пренебрежение соответствующим слагаемым по сравнению с оставленным.
Решение
примера
:
0
0
.
0
Решение
примера
:
0
.
0
Решение
примера
:
предела
не существует.
0
Здесь не существование предела связано с тем, что для четных и нечетных значений получается различные значения предела (1/4 и –1/4), что противоречит необходимости существования единственного предела.
При решении примеров были использованы свойства, приведенные в §1.