Д. Н. КАЧЕВСКИЙ
ИНТЕГРИРОВАНИЕ
СБОРНИК ТИПОВЫХ ЗАДАНИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ
Учебное пособие для студентов вузов
экономических и технических специальностей
Издание второе
Чебоксары «ДНК» 2008
К 30
УДК 517.3
Качевский Дмитрий Николаевич
К 30 Интегрирование. Сборник типовых заданий по высшей математике,- Чебоксары: ДНК, 2008, 24 с., ил.
Учебное пособие по высшей математике для студентов вузов экономических и технических специальностей. Содержит типовые контрольные задания для самостоятельной работы студентов. Задания разбиты по вариантам и включают разделы: неопределенный интеграл, определенный интеграл, дифференциальные уравнения, ряды. Каждая задача снабжена типовым примером решения.
Пособие может быть использовано студентами всех форм обучения.
© Чебоксары, «ДНК», 2008.
Предисловие ко второму изданию
Пособие предназначено для самостоятельной работы студентов вузов. Предлагаемые задачи связаны с интегрированием, его приложением к дифференциальным уравнениям и к интегрированию степенных рядов. Задачи представлены в 10 вариантах. Все варианты имеют один уровень сложности. Для каждой задачи приводится типовой пример решения под тем же номером, что и сама задача.
Пособие может быть использовано студентами дневной, вечерней и заочной форм обучения.
ИНТЕГРИРОВАНИЕ
Неопределенный интеграл.
Определенный интеграл.
Дифференциальные уравнения.
Ряды.
Задача 1. Вычислить неопределенный интеграл
Пример 1. Вычислить неопределенный интеграл
.
Решение: Искомый интеграл представляет собой сумму интегралов:
,
.
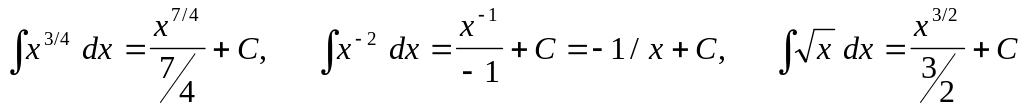При интегрировании были использованы формулы:
.
Задача 2. Вычислить неопределенный интеграл
2.1
2.2
2.3
2.3
2.4
2.5
2.6
2.7
2.8
2.9
2.10
Пример 2. Вычислить неопределенный интеграл
.
Искомый интеграл равен сумме следующих интегралов:
,
,
,
,
,
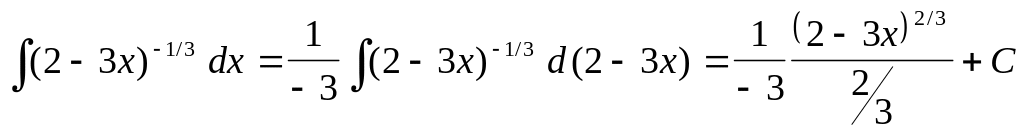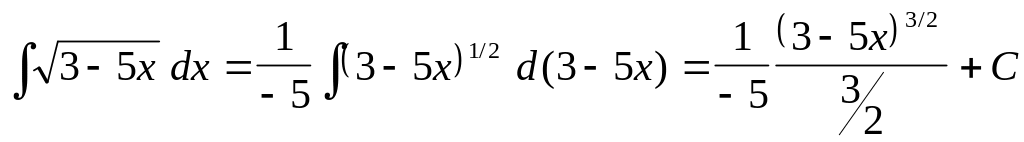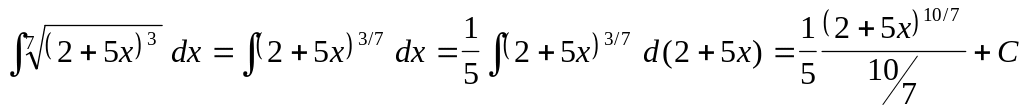Здесь помимо правила интегрирования сложной функции
были использованы табличные интегралы
,
а также свойства дифференциала:
и интеграла
,
где
.
Задача 3. Вычислить неопределенный интеграл
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
3.10
Пример 3. Вычислить неопределенный интеграл
.
Решение: Искомый интеграл равен сумме следующих интегралов:
,
,
,
,
.
Для вычисления интегралов были использованы табличные интегралы:
, 
, 
,
, 
,
а также свойство интеграла
,
где
.
Задача 4. Вычислить неопределенный интеграл
4.1
4.2
4.3
4.4
.
4.5
4.6
4.7
4.8
4.9
4.10
Пример 4. Вычислить неопределенный интеграл
.
Искомый интеграл равен сумме следующих интегралов:
,
,
,
,
.
Здесь
переменные
или
вносились под знак дифференциала с
учетом свойства дифференциала
.
При вычислении интегралов были
использованы следующие табличные
интегралы:
,
, 
,
, 
,
а также свойство интеграла
, где .
Задача 5. Вычислить неопределенный интеграл
5.1
5.2
5.3
5.4
5.5
5.6
5.7
5.8
5.9
5.10
Пример 5. Вычислить неопределенный интеграл
Решение: Искомый интеграл равен сумме следующих интегралов:
,
,
,
,
.
Здесь
для вычисления интегралов были
использованы свойства дифференциала:
свойство интеграла:
,
где 
,
а также табличные интегралы:
.
Задача 6. Проинтегрировать квадратный трехчлен
6.1
6.2
6.3
6.4
6.5
6.6
6.7
6.8
6.9
6.10
Пример 6. Проинтегрировать квадратный трехчлен
;
.
Решение:
В
квадратном трехчлене выделим полный
квадрат:
.
.
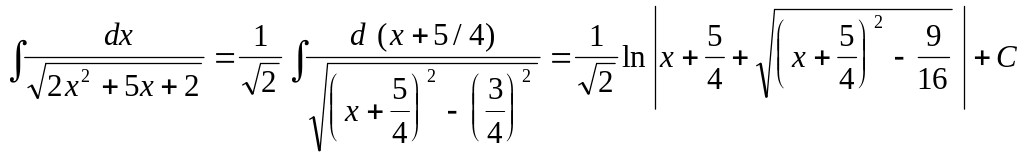Здесь был использован табличный интеграл
.
Решение:
.
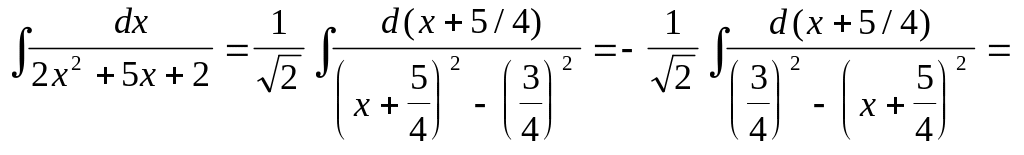
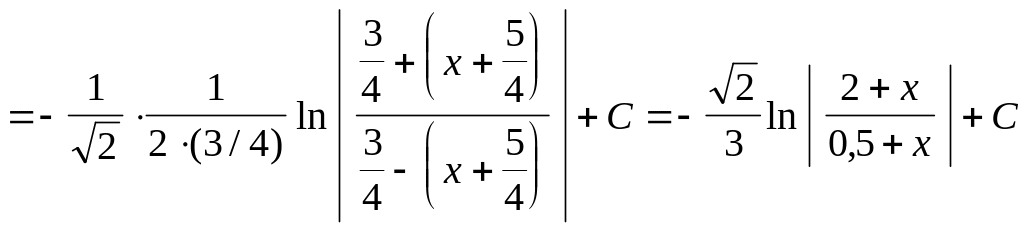Решение:
.
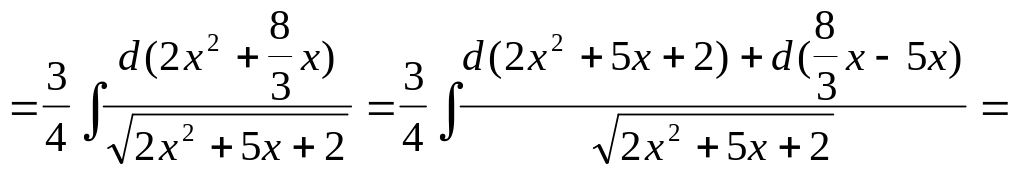
Вместо
вычисления последнего интеграла мы
воспользовались уже готовым результатом
вычисления примера
.
Здесь кроме уже встречавшихся свойств интегралов и дифференциалов было использовано свойство:
.
Решение:
Поступая также как в примере
,
вносим числитель подынтегрального
выражения под знак дифференциала. При
этом ввиду того, что имеет место равенство
,
связывающее числитель и знаменатель подынтегрального выражения, вычисление интеграла становится значительно проще, чем в примере :
.
Здесь использовался табличный интеграл
.
Задача 7. Проинтегрировать дробно-рациональную функцию
7.1
7.2
7.3
7.4
7.5
7.6
7.7
7.8
7.9
7.10
Пример 7. Проинтегрировать дробно-рациональные функции
;
.
Решение
примера
:
Поскольку дробно-рациональная функция
представляет собой неправильную дробь
(степень многочлена числителя не меньше
степени многочлена знаменателя), выделим
из дроби целую часть и правильную дробь,
у которой степень многочлена числителя
меньше степени многочлена знаменателя.
Процесс выделения протзведем с помощью
деления в столбик:
.
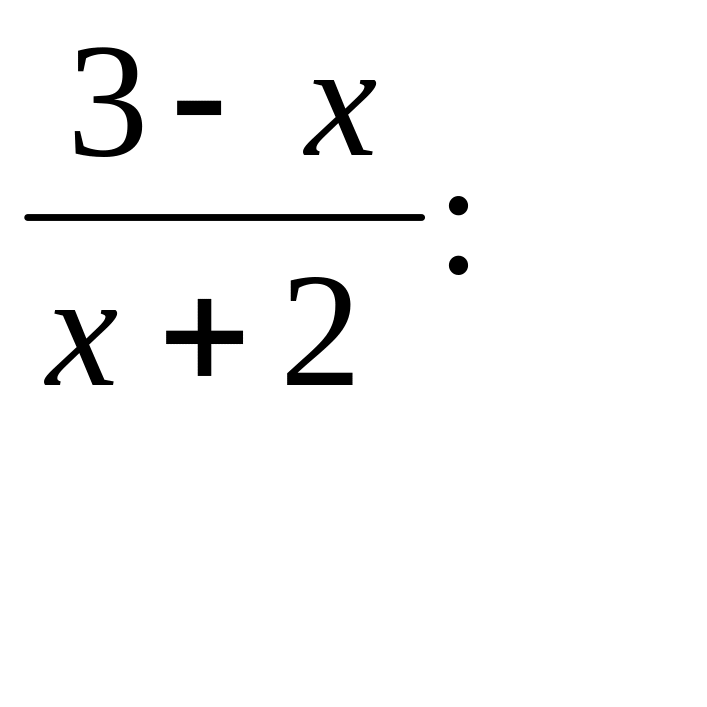
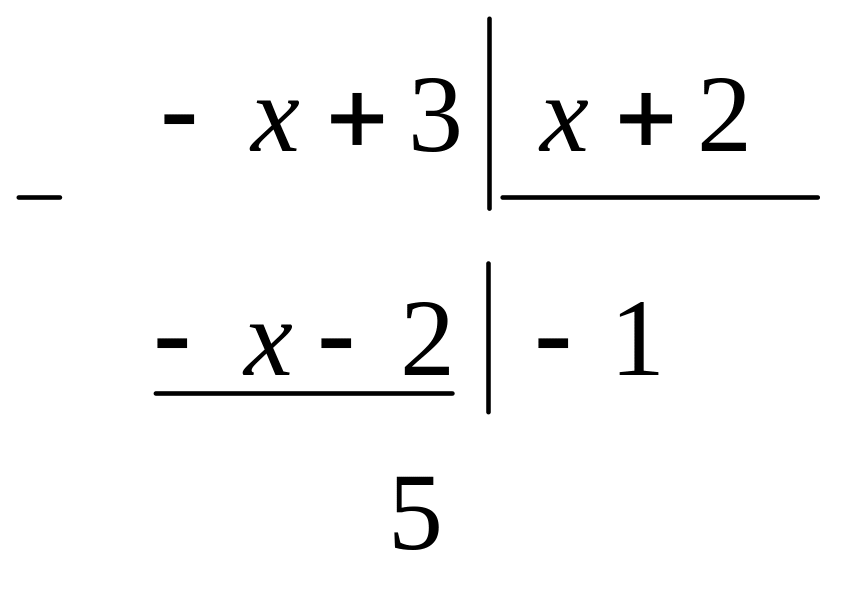
Таким образом, имеем:
.
При вычислении был использован табличный интеграл
.
Решение
примера
:
Как и в примере , неправильную дробь с помощью деления в столбик можно представить, как сумму целой части и правильной дроби. Однако вместо деления в столбик мы воспользуемся почленным делением дроби:
.
Здесь
был использован табличный интеграл
.
Решение
примера
:
Рассматриваемая дробь является правильной дробью, однако ввиду того, что знаменатель разлагается на простые множители, удобно саму дробь разложить на простые дроби. Воспользуемся для этого методом неопределенных коэффициентов:
.
В силу тождественного равенства левой и правой дроби, соответствующие коэффициенты числителей (левой и правой дроби) должны совпадать. Откуда имеем:
Решаем полученную систему двух уравнений и находим неизвестные коэффициенты.
Таким образом, заданная правильная дробь представляется суммой простых дробей:
,
откуда имеем
.
Здесь опять был использован табличный интеграл
.
Решение
примера
:
Заданная
дробно-рациональная функция
является правильной дробью. Методом
неопределенных коэффициентов разложим
ее на сумму простых дробей:
.
Приравнивая
коэффициенты перед одинаковыми степенями
числителей левой и правой дроби, получаем
систему уравнений для коэффициентов
:
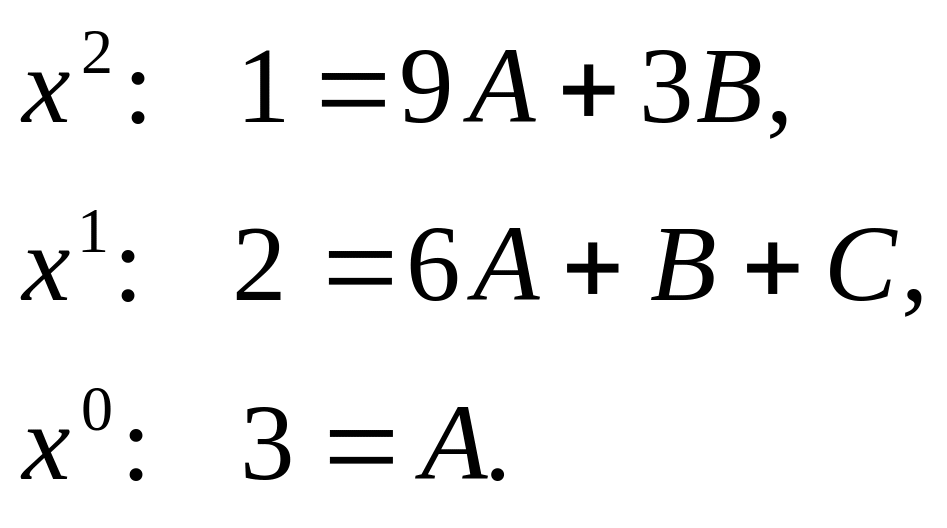
Решая систему, находим коэффициенты:
.
Таким образом, имеем разложение:
.
Здесь опять использовался табличный интеграл .
Решение
примера
:
Дробно-рациональная функция является неправильной дробью. Делением в столбик, выделяем из нее целую часть и правильную дробь:
.
При этом искомый интеграл равен:
.
Здесь был использован метод интегрирования квадратного трехчлена, который применялся при решении примера 6. Из табличных интегралов использовались:
.
Покажем, как производилось деление в столбик:
.
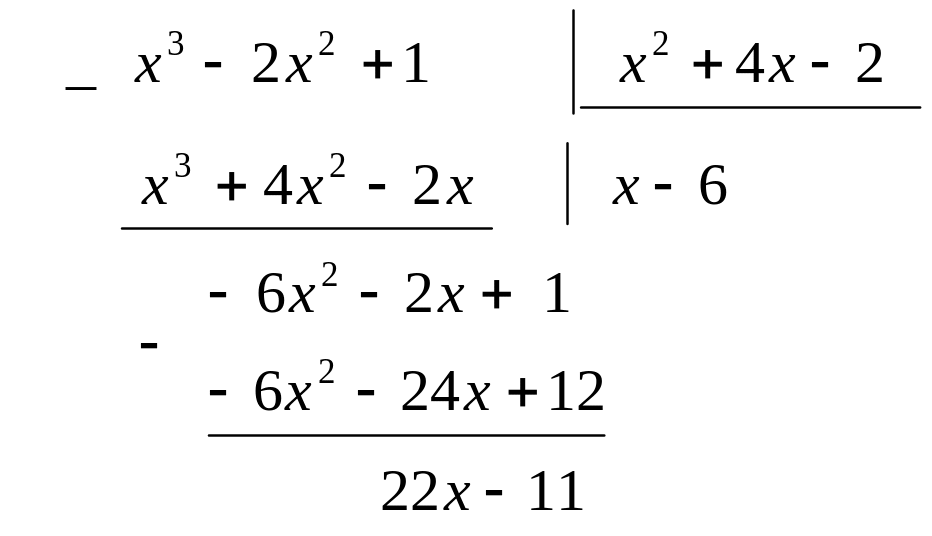Решение
примера
:
Заданная
дробно-рациональная функция
представляет собой неправильную дробь.
Делением в столбик выделяем из нее целую
часть и правильную дробь:
.
Методом неопределенных коэффициентов правильную дробь разлагаем на простые дроби:
Приравнивая
коэффициенты числителей при одинаковых
степенях
левой и правой дроби, получим систему
уравнений для нахождения коэффициентов:
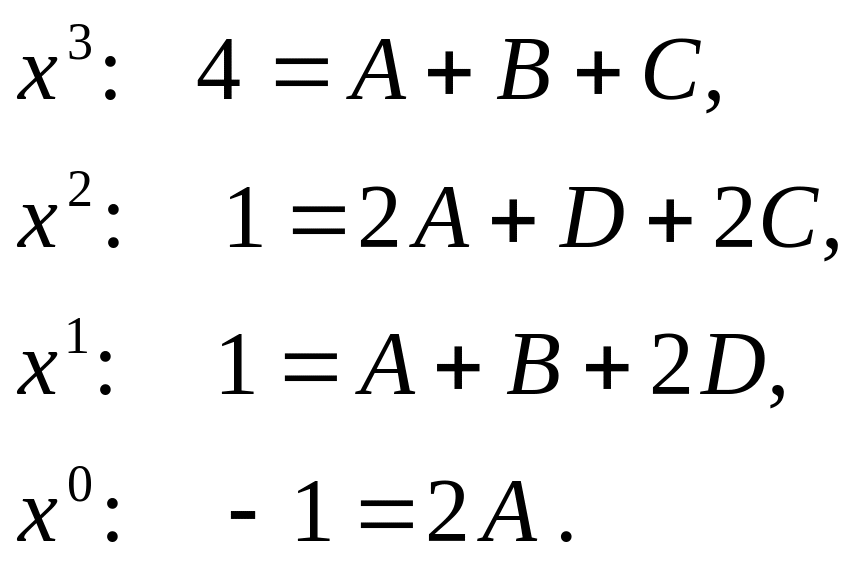
Решая систему, находим коэффициенты:
Искомый интеграл представляется в виде:
.
Из табличных были использованы интегралы:
.
Покажем еще, как проводилось деление в столбик:
.
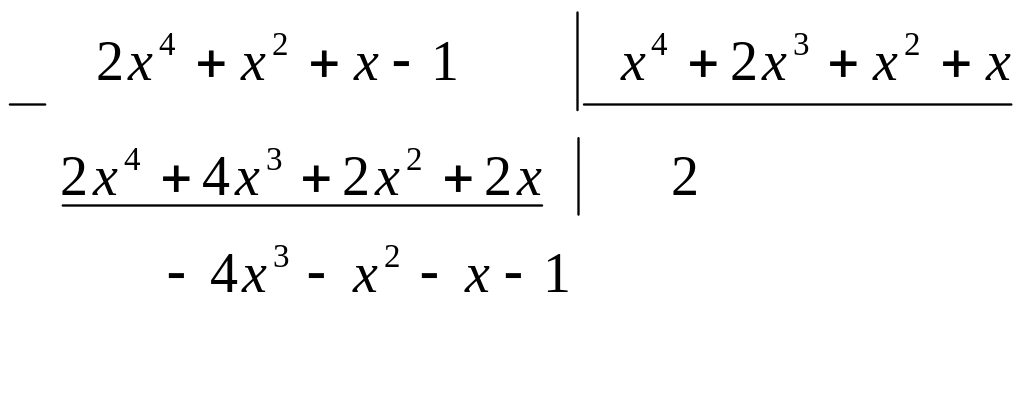Задача 8. Вычислить неопределенный интеграл
8.1
8.2
8.3
8.4
8.5
8.6
8.7
8.8
8.9
8.10
Пример 8. Вычислить неопределенные интегралы:
;
.
Все
эти интегралы вычисляются методом
интегрирования по частям, согласно
формуле 
.
Решение примера 8 :
.
Здесь были использованы табличные интегралы:
.
Решение
примера
:
.
Интегрирование
по частям здесь производилось дважды.
Использовался табличный интеграл: 
.
Решение
примера
:
.
Здесь был использован табличный интеграл
.
Решение
примера
:
.
Здесь были использованы табличные интегралы
.
Решение
примера
:
.
Здесь были использованы табличные интегралы:
.