§ 4. Функции, эквивалентные в нуле

Для бесконечно малых значений переменной , ( при ) функции, имеющие разложение в ряд Тейлора в окрестности нуля, могут быть представлены в эквивалентной форме своими рядами Тейлора:

• ; ;

• ; ;

• ;

• ;

• ;

• .

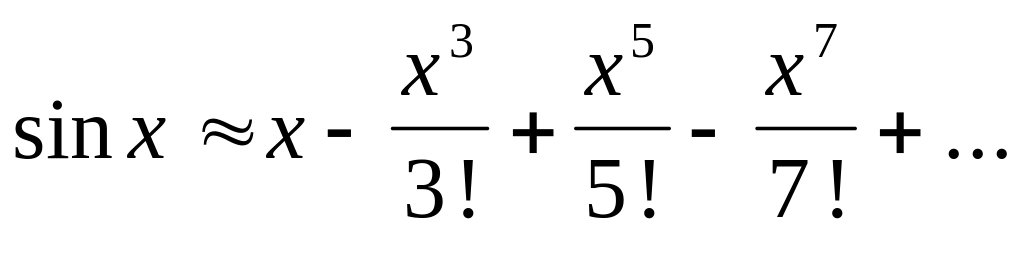Замена функций их рядами Тейлора проводится с той степенью приближения (учитывается только несколько членов ряда Тейлора), которая требуется для решения соответствующей задачи.

При вычислении пределов с использованием эквивалентных в нуле функций, старшими степенями обычно пренебрегают, оставляя лишь те степени, которые уже встречаются в алгебраическом выражении, но при этом следует учитывать, что в результате пренебрежения не должны все оставленные члены ряда взаимно уничтожаться, т. к. в этом случае получилось бы, что пренебрегли членами, по модулю меньшими нуля, что не имеет смысла.

§ 5. Основные теоремы о пределах функций

1. Предел постоянной величины равен самой этой величине:

.

2. Предел суммы (разности) конечного числа функций равен сумме (разности) их пределов

.

3. Предел произведения конечного числа функций равен произведению их пределов

.

4. Предел частного двух функций равен отношению их пределов

.

Здесь предполагается, что пределы, стоящие в правых частях равенств, существуют.

§ 6. Виды неопределенности и способы их раскрытия

Рассмотренные в § 1 правила обращения с бесконечностью и нулем

необходимо дополнить четырьмя видами неопределенности, которые в каждом конкретном случае должны быть раскрыты. Раскрытие их осуществляется с помощью вычисления соответствующих пределов.

Четыре виде неопределенности:

I. ;        II.  ;        III. ;          IV. .

Для раскрытие неопределенности вида I применяют

1. Правило Лопиталя, которое в символической форме можно представить в виде

.

Штрихи означают взятие производной от функции, стоящей в числителе и производной от функции, стоящей в знаменателе дроби, предел которой вычисляется.

Замечание. Если при использовании правила Лопиталя (т. е. после проведения дифференцирования, как числителя, так и знаменателя дроби) окажется, что предел новой полученной дроби не существует, то это не обязательно означает, что не существует

искомый предел первоначальной дроби. Это означает, что само правило Лопиталя не применимо к вычислению предела первоначальной дроби. В этом случае вычисление предела должно быть проведено другими методами, без использования правила Лопиталя.

2. Использование эквивалентных в нуле функций.

3. Алгебраические преобразования, в частности, сокращение множителей, приводящих к появлению неопределенности.

Пр.1

.

Здесь правило Лопиталя использовалось дважды, один раз при раскрытии неопределенности , другой раз при раскрытии неопределенности .

Пр. 2

.

Здесь неопределенность раскрывалась с помощью замены синуса и логарифма эквивалентными в нуле функциями по формулам предыдущего параграфа.              Необходимость оставления двух первых членов разложения в ряд Тейлора диктуется тем, что, если оставлять только одно первое слагаемое, то оно взаимно

уничтожается с имеющимся аналогичным слагаемым, и в результате отброшенные слагаемые, как бы считаются по модулю бесконечно малыми по отношению к нулю, что не имеет смысла. Пренебрежение третьим и последующими слагаемыми связано с их малости по сравнению со вторым оставленным слагаемым.

П р. 3

.

Для раскрытия неопределенности вида II применяют алгебраические преобразования, сводящие неопределенность к виду I.

В символической форме это выглядит, как

, или   .

Пр.1

.

Здесь было учтено, что . Для раскрытия неопределенности использовалось правило Лопиталя.

Пр.2

.

Здесь учтено, что . Знак минус в квадратной скобке не указан. При вычислении предела было использовано правило Лопиталя.

Для раскрытия неопределенности вида III применяют алгебраические преобразования, сводящие неопределенность к виду I. В символической форме некоторые из них можно представить, как

1. ;

2. .

Полученная неопределенность вида I раскрывается по правилу Лопиталя. В первом случае правило Лопиталя применяется отдельно для неопределенности , во втором случае применяется ко всему искомому выражению.

Пр.1

                                     .

При решении примера правило Лопиталя для раскрытия неопределенности вида I использовалось дважды. Один раз для раскрытия неопределенности , другой раз для раскрытия неопределенности вида .

Пр.2

.

При раскрытии неопределенностей вида здесь было дважды использовано правило Лопиталя.

Для раскрытия неопределенности вида IV используется основное логарифмическое тождество , а также свойство логарифма , с помощью которых функцию можно представить в виде

.

Пр. 1

.

Здесь для раскрытия неопределенности вида было использовано правило Лопиталя.

Пр. 2

. (Второй замечательный предел).

Здесь также было использовано правило Лопиталя.

Пр.3 

Здесь дважды было использовано правило Лопиталя.