Задача 9. Вычислить интеграл от тригонометрической функции
9.1
9.2
9.3
9.4
9.5
9.6
9.7
9.8
9.9
9.10
Пример
9. Вычислить интеграл от тригонометрических
функций:
,
.
При решении примера необходимо использовать основные тригонометрические тождества:
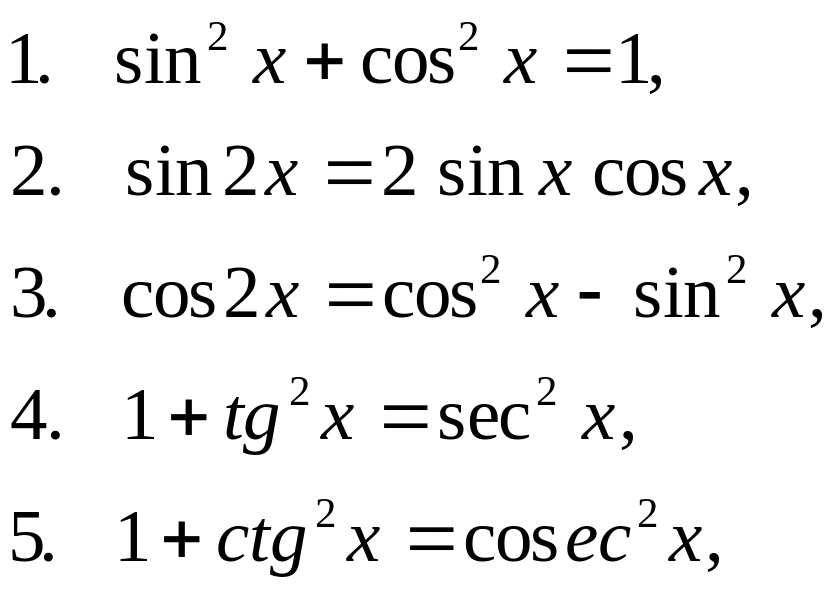
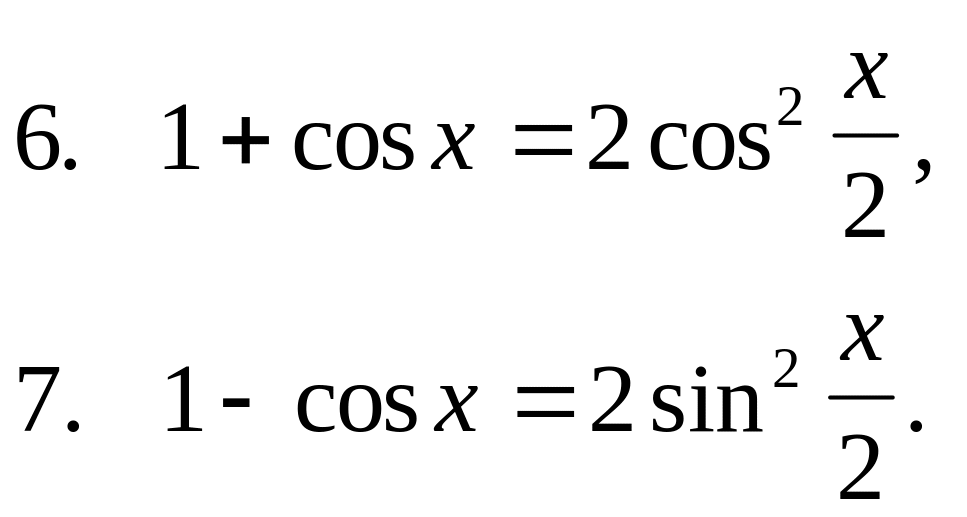
Решение:
.
Решение:
.
Решение:
.
Решение:
.
Решение:
РРешение:
.
Решение:
Здесь были использованы следующие табличные интегралы:
.
Задача 10. Вычислить интеграл с помощью замены переменной
10.1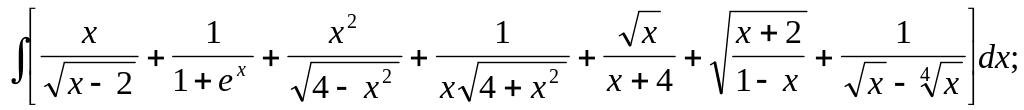
10.2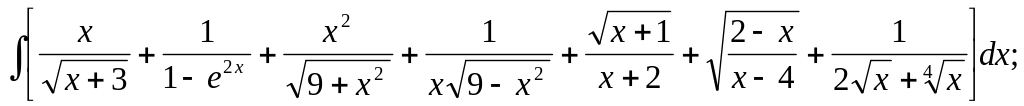
10.3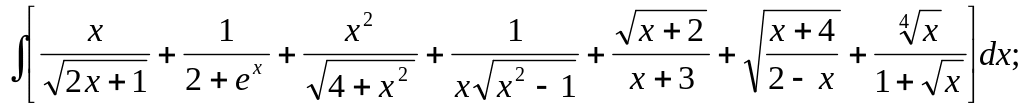
10.4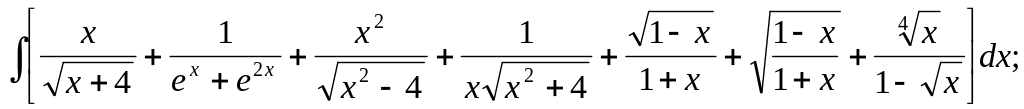
10.5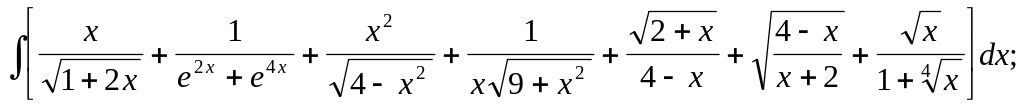
10.6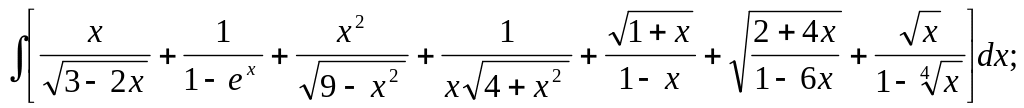
10.7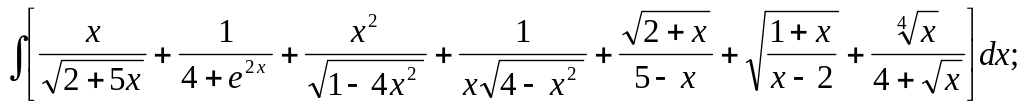
10.8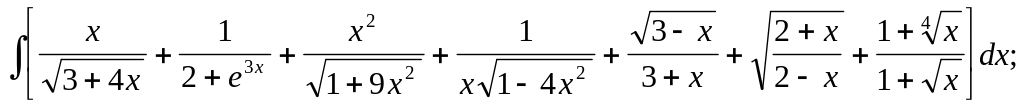
10.9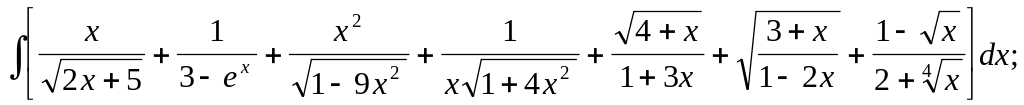
10.10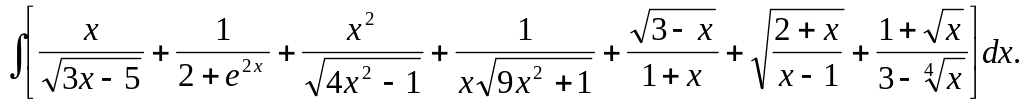
Пример 10. Спомощью замены переменной вычислить следующие интегралы:
.
Решение
примера
:
.
Решение
примера
:
,
где
.
Здесь был использован метод неопределенных коэффициентов
для разложения дробно-рациональной функции на простые дроби.
Решение
примера
:
.
Решение
примера
:
,
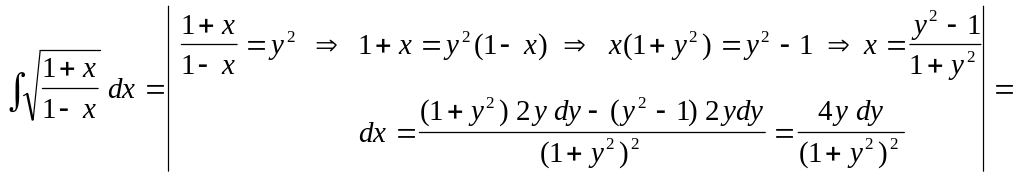
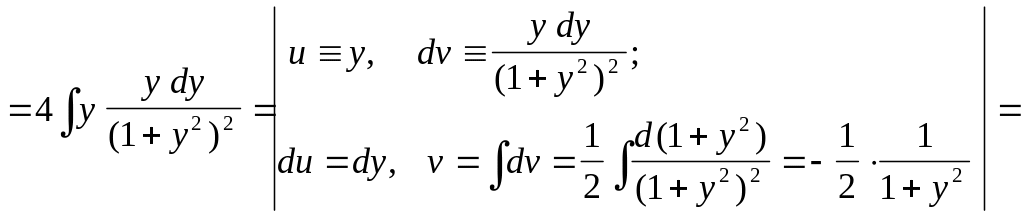
где
.
Здесь использовалось интегрирование по частям в соответствии с формулой .
Решение
примера
:
=
,
где
.
Здесь при вычислении интеграла от дробно-рациональной функции было произведено деление в столбик.
Задача 11. Найти частное решение дифференциального уравнения
11.1
11.6
11.2
11.7
11.3
11.8
11.4
11.9
11.5
11.10
Пример 11. Найти частное решение дифференциального уравнения , удовлетворяющее условию Коши .
Решение: Данное дифференциальное уравнение первого порядка является уравнением с разделяющимися переменными. Разделим переменные,
,
и
проинтегрируем полученное выражение
с помощью определенного интеграла,
учитывая условие Коши
:
.
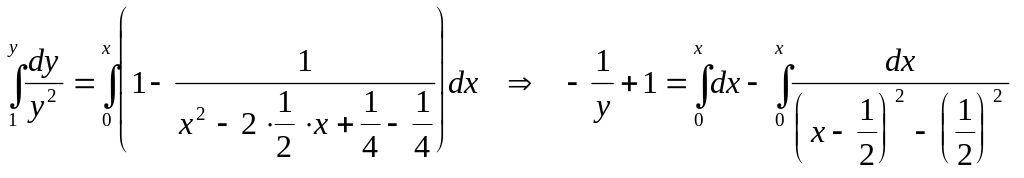Выполняя интегрирование, получаем:
.
И окончательно, частное решение дифференциального уравнения запишется в виде:
.
Задача 12. Найти общее решение дифференциального уравнения
12.1
12.6
12.2
12.7
12.3
12.8
12.4
12.9
12.5
12.10
Пример
12. Найти общее решение дифференциального
уравнения
.
Решение: Уравнение представляет собой дифференциальное уравнение Бернулли. Ищем решение в виде произведения двух неизвестных функций:
.
(очевидно,
что одну из функций можно выбрать
произвольно). Подставляя
значение
в дифференциальное уравнение,
,
у
второго и третьего слагаемого вынесем
общий множитель
за скобки
.
Потребуем,
чтобы квадратная скобка обратилась в
ноль, ( тем самым фактически задаем
уравнение, из которого можно найти
функцию
),
при этом уравнение Бернулли распадается
на два уравнения :
1) 
,
2) 
.
Из
первого уравнения находим функцию
:
,
откуда
,
или 
.
Подставляя найденное значение функции во второе уравнение,
,
получаем дифференциальное уравнение с разделяющимися переменными:
,
интегрирование которого, произведем с помощью неопределенного интеграла:
.
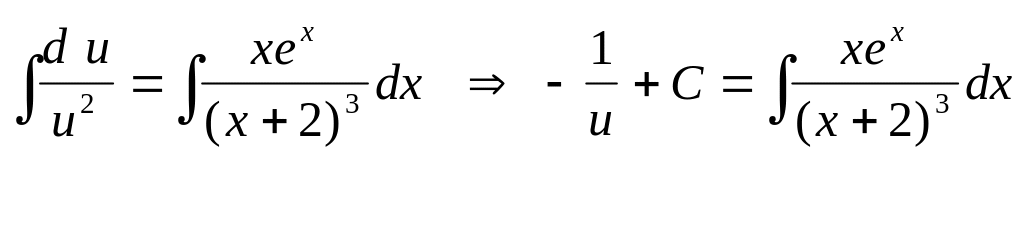Интеграл по переменной через элементарные функции не выражается, поэтому его оставляем без изменения. Для функции получаем выражение:
.
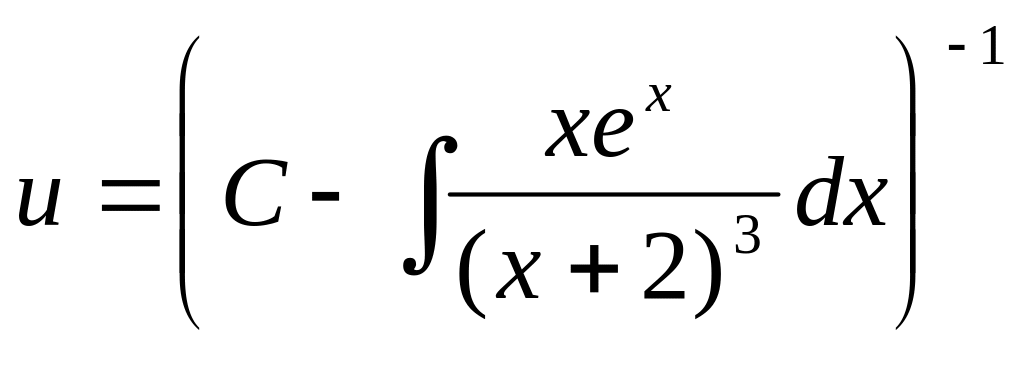Таким
образом, обе неизвестные функции
и
найдены. Для искомой функции
получаем окончательное выражение:
,
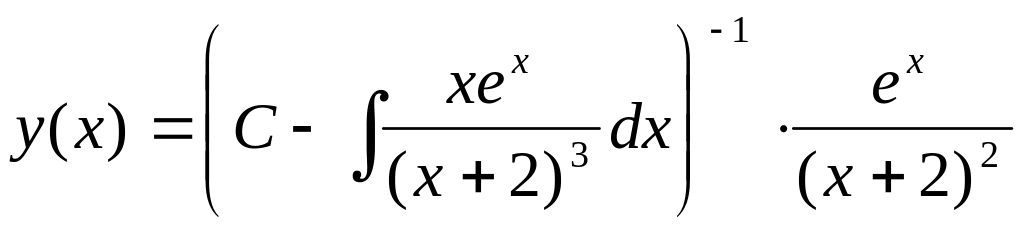которое и представляет собой общее решение дифференциального уравнения Бернулли.
Задача
13. Найти сумму сходящегося ряда с
точностью до
13.1
13.6
13.2
13.7
13.3
13.8
13.4
13.9
13.5
13.10
Пример
13. Найти сумму сходящегося ряда
с точностью до
.
Решение:
Данный числовой ряд является
знакочередующимся и, начиная с
последующие члены ряда не превосходят
предыдущего, а также
ый
член ряда стремится к нулю при
,
т. е. выполняются условия теоремы
Лейбница, и поэтому сумма ряда приближенно
равна сумме его первых
членов, допускаемая при этом погрешность
по абсолютной величине не превосходит
первого отброшенного члена
.
...
.
Ввиду
того, что
для приближенного вычисления суммы
ряда
с заданной точностью достаточно сложить
первые восемь членов ряда .
Таким образом, имеем
.
Задача 14. Найти сумму степенного ряда
14.1
14.6
14.2
14.7
14.3
14.8
14.4
14.9
14.5
14.10