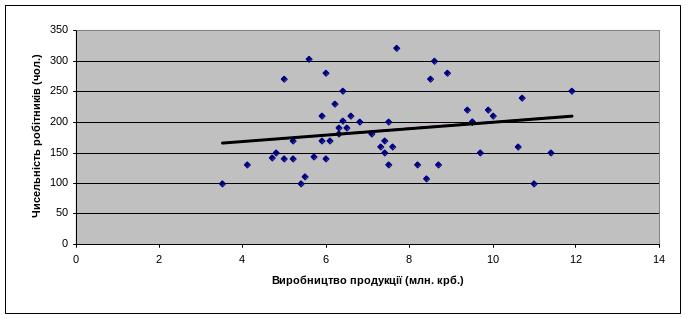
7. Побудова спряженої кореляційно-регресійної моделі
Якщо за факторну ознаку взяти виробництво продукції підприємтсрв. А за результуючу – чисельність робітників, то можна побудувати рівняння прямої регресії x на y:
,
яке називають спряженим до рівняння регресії y на x.
Параметри
і
можна знайти декількома способами
аналогічно параметрам
та
:
за допомогою формули:
З цієї формули випливає, що:
Модуль розкриваємо зі знаком коефіцієнта регресії.
визначаємо
з формули:
За обома способами отримуємо:
=
5,297 (робочих/ млн. крб.)
=
147,3989 (робочих)
Спряжену кореляційно-регресійну модель можна зобразити так:
=147,3989+5,297y
На основі аналізу коефіцієнта регресії = 5,297 (робочих/ млн. крб.) можна зробити наступні висновки:
оскільки він відмінний від 0, то на підставі вибірки можна стверджувати,що між виробництвом продукції та чисельністю працівників на підприємтсвах існує лінійна кореляційна залежність;
оскільки значення
додатнє, то при збільшенні виробництва
продукції
середнє значення чисельністі працівників
в середньому зростає;при збільшенні виробництва продукції на 1 млн. крб. середнє значення чисельністі працівників на підприємтсвах в середньому зросте на 5 працівників.
Вільний член рівняння регресії показує нам ,що при відсутності виробництва продукції – в середньому чисельність працівників на підприємтсвах буде становити 147 (робочих).
Розрахуємо теоретичні значення величини виробничих фондів на основі спряженої моделі:
Таблиця 8. Теоретичні значення величини виробничих фондів, млн.крб. на основі побудованого спряженого рівняння регресії
№ п/п |
Чисельність робітників чол. (фактичні значення) |
Чисельність робітників чол. (нормативні значення) |
1 |
270 |
173,88392 |
2 |
280 |
179,18093 |
3 |
210 |
200,36894 |
4 |
320 |
188,18583 |
5 |
160 |
203,54714 |
6 |
130 |
193,48283 |
7 |
170 |
178,65123 |
8 |
220 |
197,19074 |
9 |
200 |
187,12643 |
10 |
100 |
176,00272 |
11 |
150 |
207,78474 |
12 |
210 |
178,65123 |
13 |
200 |
197,72044 |
14 |
300 |
192,95313 |
15 |
140 |
173,88392 |
16 |
170 |
179,71063 |
17 |
130 |
190,83433 |
18 |
200 |
197,72044 |
19 |
150 |
172,82452 |
20 |
100 |
165,93842 |
21 |
160 |
187,65613 |
22 |
190 |
180,77003 |
23 |
210 |
182,35913 |
24 |
130 |
187,12643 |
25 |
240 |
204,07684 |
26 |
250 |
181,29973 |
27 |
160 |
186,06703 |
28 |
130 |
169,11662 |
29 |
140 |
179,18093 |
30 |
150 |
186,59673 |
31 |
220 |
199,83924 |
32 |
170 |
186,59673 |
33 |
100 |
205,66594 |
34 |
170 |
174,94332 |
35 |
230 |
180,24033 |
36 |
200 |
183,41853 |
37 |
280 |
194,54224 |
38 |
180 |
185,00763 |
39 |
140 |
174,94332 |
40 |
202 |
181,29973 |
41 |
270 |
192,42343 |
42 |
150 |
198,77984 |
43 |
143 |
177,59182 |
44 |
141 |
172,29482 |
45 |
302 |
177,06212 |
46 |
110 |
176,53242 |
47 |
250 |
210,43325 |
48 |
180 |
180,77003 |
49 |
108 |
191,89373 |
50 |
190 |
181,82943 |
Малюнок 3 Спряжена пряма регресії, яка описує залежність чисельності працівників (чол..) від виробництва продукції (млн. крб.) на підприємтсвах.