Міністерство освіти і науки, молоді та спорту України

Прикарпатський національний університет

імені Василя Стефаника

Кафедра радіофізики і електроніки

Лабораторна робота №7

з дисципліни

"Алгоритми та методи обчислень"

Реалізація графів

Івано-Франківськ – 2011

Мета роботи:

- оволодіти навичками роботи з алгоритмами обходу графа;

- навчитися вирішувати завдання обходу графа на основі пошуку в ширину і пошуку в глибину.

Теоретичні відомості

Ключові терміни:

Граф - це сукупність двох кінцевих множин: множина точок і множина ліній, що попарно з'єднують деякі із цих точок. Множина точок називається вершинами (вузлами) графа. множина ліній, що з'єднують вершини графа, називаються ребрами (дугами) графа.

Орієнтований граф (орграф) - це граф, у якого всі ребра орієнтовані, тобто ребрам якого привласнений напрямок.

Неорієнтований граф (неорграф) - граф, у якого всі ребра неорієнтовані, тобто ребрам якого не заданий напрямок.

Змішаний граф - це граф, який містить як орієнтовані, так і неорієнтовані ребра.

Вершини (вузли) графа - це множини точок, що утворюють граф.

Ребра (дуги) графа - це множина ліній, що з'єднують вершини графа.

Петля - це ребро, що з'єднує вершину саму із собою.

Список ребер - це множина, утворена парами суміжних вершин.

Суміжні вершини - це вершини, з'єднані загальним ребром.

Кратні ребра - це ребра, що з'єднують ту саму пару вершин.

Простий граф - це граф, у якому немає ні петель, ні кратних ребер.

Мультиграф - це граф, у якого будь-які дві вершини з'єднані більш ніж одним ребром.

Вага (довжина) ребра - це число або кілька чисел, які інтерпретуються стосовно ребра як довжина, пропускна здатність і т. д.

Вага вершини - це число (дійсне, цілу або раціональне), поставлене у відповідність даній вершині (інтерпретується як вартість, пропускна здатність і т.д. ).

Зважений граф - це граф, кожному ребру якого поставлено у відповідність якесь значення (його вага).

Маршрут у графі - це кінцева послідовність суміжних вершин і ребер, які з'єднують ці вершини, що чергуються.

Замкнутий маршрут - це маршрут у графі, у якому початкова і кінцева вершини збігаються.

Відкритий маршрут - це маршрут у графі, у якого початкова і кінцева вершини різні.

Ланцюг - це маршрут у графі, у якому всі ребра різні.

Шлях - це відкритий ланцюг, у якої всі вершини різні.

Цикл - це замкнутий ланцюг, у якому всі його вершини різні, за винятком кінцевих.

Зв'язний граф - це граф, у якому для будь-якої пари вершин існує з'єднуючий їх шлях.

Тупик - це вершина графа, для якої всі суміжні з нею вершини вже відвідані.

Матриця інцидентності - це двовимірний масив, у якому вказуються зв'язки між інцидентними елементами графа (ребро і вершина).

Матриця суміжності - це двовимірний масив, значення елементів якого характеризуються суміжністю вершин графа

Обхід графа (пошук на графі) - це процес систематичного перегляду всіх ребер або вершин графа з метою відшукання ребер або вершин, що задовольняють деякій умові.

Пошук у глибину - це обхід графа по можливим шляхам, коли потрібно спочатку повністю досліджувати одну гілку і тільки потім переходити до інших гілок (якщо вони залишаться нерозглянутими).

Пошук в ширину - це обхід графа по можливим шляхам, коли після відвідування вершини, відвідуються всі сусідні з нею вершини.

Теорія графів останнім часом широко використається в різних галузях науки і техніки. Швидкий розвиток дана теорія одержала зі створенням електронно-обчислювальної техніки, яка дозволяє вирішити багато завдань алгоритмізації.

Вибір структури даних для зберігання графа в пам'яті комп'ютера має принципове значення при розробці ефективних алгоритмів. Розглянемо кілька способів подання графа.

Нехай заданий граф (наприклад, рис. 1), у якого кількість вершин дорівнює n, а кількість ребер - m. Кожне ребро і кожна вершина мають вагу - ціле додатне число. Якщо граф не є позначеним, то вважається, що вага дорівнює одиниці.

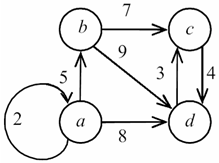
Рисунок 1.  Граф

Список ребер - це множина, утворена парами суміжних вершин (рис. 2). Для його зберігання звичайно використовують одновимірний масив розміром m, що містить список пар вершин, суміжних з одним ребром графа. Список ребер більш зручний для реалізації різних алгоритмів на графах у порівнянні з іншими способами.

Рисунок 2.  Список ребер графа

Матриця суміжності - це двовимірний масив розмірності n  n, значення елементів якого характеризується суміжністю вершин графа (рис. 3). При цьому значенню елемента матриці привласнюється кількість ребер, які з'єднують відповідні вершини. Даний спосіб дійовий, коли треба перевіряти суміжність або знаходити вагу ребра по двом заданим вершинам.

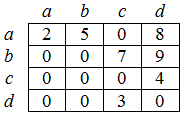
Рисунок 3.  Матриця суміжності графа

Матриця інцидентності - це двовимірний масив розмірності n  m, у якому вказуються зв'язки між інцидентними елементами графа (ребро і вершина). Стовпчики матриці відповідають ребрам, рядки - вершинам (рис. 4). Ненульове значення в комірці матриці вказує зв'язок між вершиною і ребром. Даний спосіб є самим ємним для зберігання, але полегшує знаходження циклів у графі.

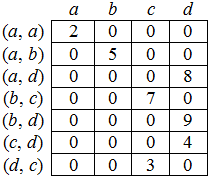
Рисунок 4.  Матриця інцидентності графа

Існує багато алгоритмів на графах, в основі яких лежить систематичний перебір вершин графа, такий що кожна вершина проглядається (відвідується) у точності один раз. Тому важливим завданням є знаходження гарних методів пошуку в графі.

Під обходом графів (пошуком на графах) розуміється процес систематичного перегляду всіх ребер або вершин графа з метою відшукання ребер або вершин, які задовольняють деякій умові.

При рішенні багатьох завдань, що використовують графи, необхідні ефективні методи регулярного обходу вершин і ребер графів. До стандартного і найпоширеніших методів відносяться:

- пошук у глибину (Depth Fіrst Search, DFS);

- пошук в ширину (Breadth Fіrst Search, BFS).

Ці методи найчастіше розглядаються на орієнтованих графах, але вони застосовуються і для неорієнтованих, ребра яких вважаються двохнаправленими. Алгоритми обходу в глибину і в ширину лежать в основі рішення різних завдань обробки графів, наприклад, побудови остовного лісу, перевірки зв’язності, ациклічності, обчислення відстаней між вершинами і інших.

Пошук у глибину. При пошуку в глибину відвідується перша вершина, потім необхідно йти уздовж ребер графа, до влучення в тупик. Вершина графа є тупиком, якщо всі суміжні з нею вершини вже відвідані. Після влучення в тупик потрібно вертатися назад уздовж пройденого шляху, поки не буде виявлена вершина, у якій є ще не відвідана вершина, а потім необхідно рухатися в цьому новому напрямку. Процес виявляється завершеним при поверненні в початкову вершину, причому всі суміжні з нею вершини вже повинні бути відвідані.

Таким чином, основна ідея пошуку в глибину - коли можливі шляхи по ребрам, що виходять із вершин, розгалужуються, потрібно спочатку повністю досліджувати одну гілку і тільки потім переходити до інших гілок (якщо вони залишаться нерозглянутими).

Алгоритм пошуку в глибину

Крок 1. Всім вершинам графа привласнюється значення, яке позначає не відвідуваність. Вибирається перша вершина і позначається як відвідана.

Крок 2. Для останньої позначеної як відвідана вершини вибирається суміжна вершина, що є першою позначеною як не відвідана, і їй привласнюється значення відвідана. Якщо таких вершин немає, то береться попередня позначена вершина.

Крок 3. Повторити крок 2 доти, поки всі вершини не будуть позначені як відвідані (рис. 5).

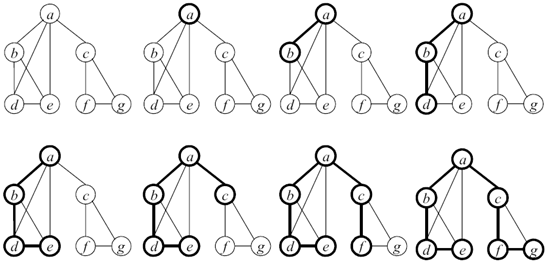
Рисунок 5.  Демонстрація алгоритму пошуку в глибину

// Опис функції алгоритму пошуку в глибину

void Depth_First_Search(int n, int **Graph, bool *Visited,

int Node){

Visited[Node] = true;

cout << Node + 1 << endl;

for (int i = 0 ; i < n ; i++)

if (Graph[Node][i] && !Visited[i])

Depth_First_Search(n,Graph,Visited,i);

}

Також часто використовується нерекурсивний алгоритм пошуку в глибину. У цьому випадку рекурсія замінюється на стек. Як тільки вершина переглянута, вона заноситься у стек, а використаною вона стає, коли більше немає нових вершин, суміжних з нею.

Пошук в ширину. При пошуку в ширину, після відвідування першої вершини, відвідуються всі сусідні з нею вершини. Потім відвідуються всі вершини, що перебувають на відстані двох ребер від початкової. При кожному новому кроці відвідуються вершини, відстань від яких до початкової на одиницю більше попереднього. Щоб запобігти повторному відвідуванню вершин, необхідно вести список відвіданих вершин. Для зберігання тимчасових даних, необхідних для роботи алгоритму, використовується черга - впорядкована послідовність елементів, у якій нові елементи додаються в кінець, а старі вилучаються з початку.

Таким чином, основна ідея пошуку в ширину полягає в тому, що спочатку досліджуються всі вершини, суміжні з початковою вершиною (вершина з якої починається обхід). Ці вершини перебувають на відстані 1 від початкової. Потім досліджуються всі вершини на відстані 2 від початкової, потім усе на відстані 3 і т.д. Зверніть увагу, що при цьому для кожної вершини відразу знаходиться довжина найкоротшого маршруту від початкової вершини.

Алгоритм пошуку в ширину

Крок 1. Всім вершинам графа привласнюється значення не відвідана. Вибирається перша вершина і позначається як відвідана (і заноситься в чергу).

Крок 2. Відвідується перша вершина із черги (якщо вона не позначена як відвідана). Всі її сусідні вершини заносяться в чергу. Після цього вона вилучається із черги.

Крок 3. Повторюється крок 2 доти, поки черга не порожня (рис. 6).

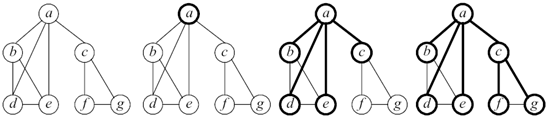
Рисунок 6.  Демонстрація алгоритму пошуку в ширину

// Опис функції алгоритму пошуку в ширину

void Breadth_First_Search(int n, int **Graph,

bool *Visited, int Node){

int *List = new int[n]; //черга

int Count, Head; // вказівники черги

int i;

// початкова ініціалізація

for (i = 0; i < n ; i++)

List[i] = 0;

Count = Head = 0;

// розміщення в чергу вершини Node

List[Count++] = Node;

Visited[Node] = true;

while ( Head < Count ) {

// взяття вершини із черги

Node = List[Head++];

cout << Node + 1 << endl;

// перегляд всіх вершин, пов'язаних з вершиною Node

for (i = 0 ; i < n ; i++)

// якщо вершина раніше не переглянута

if (Graph[Node][i] && !Visited[i]){

// заносимо її в чергу

List[Count++] = i;

Visited[i] = true;

}

}

}

Методичні вказівки

В даній роботі пропонується написати програму обраною мовою програмування, у якій скористатися алгоритмами обходу графа відповідно до завдання.

Завдання необхідно вирішити відповідно до вивчених алгоритмів обходу графа.

При виконанні лабораторної роботи для кожного завдання потрібно написати програму, що одержує на вході числові дані, виконує їхню обробку відповідно до вимог завдання і виводить результат на екран. Для обробки даних необхідно реалізувати алгоритми обходу графа відповідно до постановки завдання. Введення даних здійснюється із файлу з урахуванням вимог до вхідних даних, що міститься в постановці завдання (введення даних супроводжуйте діалогом). Обмеженнями на вхідні дані є припустимий діапазон значень використовуваних числових типів у обраній мові.

При написанні програми виконуйте коментування коду.

Література

1. Ахо А., Хопкрофт Дж., Ульман Дж. Структуры данных и алгоритмы. – М.: Издательский дом “Вильямс”, 2001. – 384 с.

2. Вирт Н. Структуры данных и алгоритмы. С примерами на Паскале. Издание 2. – СПб.: Невский диалект, 2008. – 352 с.

3. Кнут Д. Искусство программирования для ЭВМ / В 3-х томах. – М.: “Мир”, 2008.

4. Новиков Ф. А. Дискретная математика для программистов. Учебник для вузов. 2-е изд. – СПб.: Питер, 2005. – 364 с.

Завдання

1. Вивчіть словесну постановку завдання, виділивши при цьому всі види даних;

4. Сформулюйте математичну постановку завдання;

5. Виберіть метод рішення завдання, якщо це необхідно;

6. Методом обходу графа на основі пошуку в глибину та обходу графа на основі пошуку в ширину, розробіть програму для рішення завдання.

7. Запишіть розроблений алгоритм обраною мовою;

8. Розробіть контрольний тест до програми;

9. Налагодьте програму;

10. Представте звіт роботі.

11. Програму супроводьте коментарями в коді.

Вимоги до звіту

Звіт до лабораторної роботи повинен відповідати наступній структурі:

- титульний лист.

- словесна постановка завдання. У цьому підрозділі проводиться повний опис завдання. Описується суть завдання, аналіз вхідних даних, область їх припустимих значень, одиниці їхнього виміру, можливі обмеження, аналіз умов при яких завдання має рішення (не має рішення), аналіз очікуваних результатів.

- математична модель. У цьому підрозділі вводяться математичні описи даних і математичний опис їхньої взаємодій. Ціль підрозділу - подати розв'язуване завдання у математичному формулюванні.

- алгоритм рішення завдання. У підрозділі описується розробка структури алгоритму, обґрунтовується абстракція даних, завдання розбивається на підзадачі.

- лістинг програми. Підрозділ повинен містити текст програми обраною мовою програмування.

- контрольний тест. Підрозділ містить набори вихідних даних і отримані в ході виконання програми результати.

- висновки по лабораторній роботі.

- відповіді на контрольні питання.

Приклад виконання роботи

Розфарбування вершин графа. Розфарбуванням графа називається функція f: v -> {l, 2, ..., к}, яка ставить кожній вершині у відповідність деяке число (тут до належить безлічі натуральних чисел).

Розфарбування називається правильним тоді і тільки тоді, коли для будь-яких суміжних вершин i та j виконується нерівність f (i)! =f (j).

Граф, для якого існує правильне розфарбування, називається k-розфарбовуваним. Мінімальне число k, при якому граф G є k-розфарбовуваним, називається хроматичним числом.

При розфарбовуванні вершин графа їм буде задаватися деяка мітка, що називається кольором вершини. Розглянемо алгоритм розфарбовування вершин.

Нехай на першому кроці всі вершини розфарбовані в нульовий колір. Тепер будемо поступово розфарбовувати кожну вершину в кольори від 1 до k.

На кожному кроці будемо зафарбовувати чергову вершину в мінімально можливий колір, тобто якщо вершина i не має кольору, то вона зафарбовується мінімальним кольором k, причому жодна вершина з оточення i не повинна бути розфарбована таким кольором.

Даний алгоритм розфарбування називається послідовним. Необхідно відзначити, що при послідовному розфарбуванні вершин графа кількість використаних кольорів не буде мінімальним.

Алгоритм послідовного зафарбування дуже схожий на обхід в ширину. Далі представлений код програми, що реалізується мовою С++.

#include <iostream.h>

#include <conio.h>

#include <fstream.h>

int Find(int, int[]); // Прототип функції

int i, j;

int Start, N, M, k, p

main()

{

int *Colors; // Оголошує масив для зберігання кольорів,

// у які пофарбовані вершини на даному кроці

int *FIFO; // Оголошує структуру даних "черга"

int **Graf; // Оголошує матрицю суміжності графа

int *Set; // Оголошує масив для зберігання множини

// кольорів, у які вже пофарбовані вершини

ifstream input ("input.txt"); // Відкриває файл для

// читання даних

input»N»M; // Читає з файлу

// N — кількість вершин у графі,

// М — кількість ребер у графі.

// Виділяє динамічну пам'ять для матриці

N*N Graf=new int *[N]; for (i=0; i<N; i++)

Graf[i]=new int [N];

// Оголошує всі елементи матриці

for (i=0; i<N; i++)

for (j=0; j<N; j++)

Graf[i][j]=0;

for (k=0; k<M; k++)

{

input»i»j; // Читає номери суміжних вершин

Graf[i][j]=l; // Задає матрицю суміжності

}

Colors=new int [N]; // Виділяє динамічну пам'ять

// для масиву, призначеного

// для зберігання кольорів,

// у які фарбуються вершини

// на даному кроці

// Виділяє динамічну пам'ять для

// черги, що складає з N елементів

FIFO=new int [Щ;

Set=new int [N]; // Виділяє динамічну пам'ять для

// масиву, що зберігає множину кольорів,

// у які вже пофарбовані вершини

// Обнуляє всі елементи масивів,

//для яких пам'ять була

// виділена динамічно

for (i=0; i<N; i++)

{

Colors[i]=0,•

FIFO[i]=0;

Set[i]=0;

}

Start=0; // Вибирає початкову вершину

Colors[Start]=1; // і розфарбовує її в колір 1

р=0; // Вказівник на початок черги

к=1; // Вказівник на кінець черги

FIFO[p]=Start; // Заносимо стартову вершину в чергу

while (р!=к)

{

cur=FIFO[р]; // Виділяє чергову вершину із черги

р++; // Переміщує вказівник початку на одиницю

for (i=0; i<N; i++)

if (Graf[cur][i]==l && Colors[i]==0)

{

FIFO[k]=i; // Заносить вершину в чергу

k++; // Переміщує вказівник кінця черги

pos=0; // Формуємо множину кольорів,

// у які пофарбовані суміжні вершини

for (j=0; j<N;

if (Graf[FIFO[k-l]][j]==l && Colors[j]!=0)

{

Set[pos]=Colors[ j ];

pos++;

}

Colors[i] =Find(pos,Set) ; // Офарблює вершину в

// мінімально можливий колір

}

}

// Виводить результат

for (i=0; i<N; i++)

cout«Colors[i]«" ",-getch(); // Затримує екран

return 0; // Завершує роботу програми

}

int Find(int pos, int Set[]) // Опис функції,

// яка виконує пошук мінімального номера кольору,

// у який можна офарбити вершину i

{

int Min_Color, i, p;

Min_color=0;

do

{

Min_COlor++; P=0;

for (i=0; i<pos; i++) if (Set[iJ==Min_color)

{

P=l;

break;

}

} While (p!=0);

return Min_color; // Повертає мінімальний колір,

// у який можна офарбити вершину

}

Відмінність даного алгоритму від пошуку в ширину полягає лише в тому, що після того, як вершина і, суміжна з cur, заноситься в чергу, будується така множина set, елементи якої дорівнюють кольорам, у які розфарбовані суміжні з і вершини:

for (j=0; j<N; j++)

if (Graf[FIFO[k-l]][j]==l && Colors[j]!=0)

{

Set[pos]=Colors[j ];

pos++;

}

Після того як множина буде побудована, викликається функція Fіnd (іnt), яка повертає мінімальний номер кольору, у який можна пофарбувати вершину і:

int Find(int pos, int Set)

{

int Min_color, i, p;

Min_color=0;

do

{

Min_COlor++;

P=0;

for (i=0; i<pos; i++)

if (Set[i]==Min_color)

{

p=l;

break;

}

}

while (p!=0);

return Min_color;

}