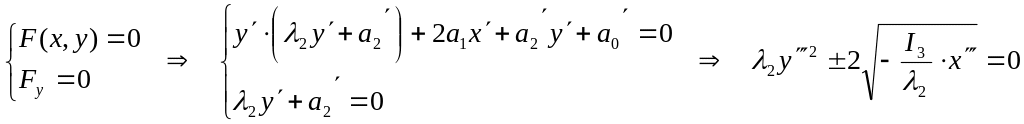1. Пряма на площині. Площина і пряма в просторі. Взаємне розміщення площин, прямих і площин в просторі.

Нехай пряма (на площині чи в просторі) проходить через задану точку паралельно заданому ненульовому в-ру , який наз. напрямним в-ром прямої. Точка і її напрямний ве-р цілком визначають пряму, паралельно в-ру . Складемо р-ня цієї прямої. Позначимо через довільну точку прямої і розглянемо радіуси-вектори та точок та і в-р , що лежить на даній прямій. Оскільки в-ри = і колінеарні, то = , звідки (1)–векторне параметричне р-ня прямої. Якщо пряма задається т. та напрямним в-ром , то, прирівнюючи відповідні координати векторів та за ф-лою (1), маємо: –параметричні р-ня прямої, звідки канонічне рня. Якщо пряма не , то р-ня (3) можна записати: або . Позначимо , тоді (4)–р-ня прямої, яка проходить через задану точку і має заданий кутовий коефіцієнт. (5)–р-ня прямої з кутовим коефіцієнтом. Рівняння прямої, яка проходить через дві задані точки , дістанемо з р-ня прямої, що проходить через точку і має напрямний вектор (6). Якщо пряма проходить через точки , тобто відтинає на осях відрізки та , то (7)–р-ня прямої у відрізках на осях. Розглянемо р-ня прямої, яка проходить через задану точку перпендикулярно до заданого ненульового вектора нормальний в-р прямої. (8)–р-ня прямої, що проходить через задану точку перпендикулярно до заданого в-ра. Загальне р-ня прямої . Це р-ня I-го степеня. Чи всяке р-ня (*) задає пряму? Нехай – розв’язок р-ня (*). . (*)–(**) . Нехай || , де – деяка пряма( ). Отримаємо колінеарні. пряма проходить через початок координат; вісь ; вісь ; отже ; отже .

Кут між двома прямими. а) Нехай прямі задано канонічними рівняннями: і –кут між цими прямими, .Оскільки в-ри і є напрямними в-рами даних прямих і , тоді маємо

(1). Якщо || , то || , тому їх координати пропорційні, тобто –умова паралельності двох прямих. Якщо , то і їхній скалярний добуток = нулю, отже, умова перпендикулярності двох прямих. б) Нехай прямі задано загальними р-ми: , тоді кут між ними = куту між їхніми нормальними векторами , тому ; – умова паралельності прямих ; – умова перпендикулярності прямих . в) Нехай прямі задані р-ми з кутовими коефіцієнтами , де – кутові коефіцієнти.

Отже, 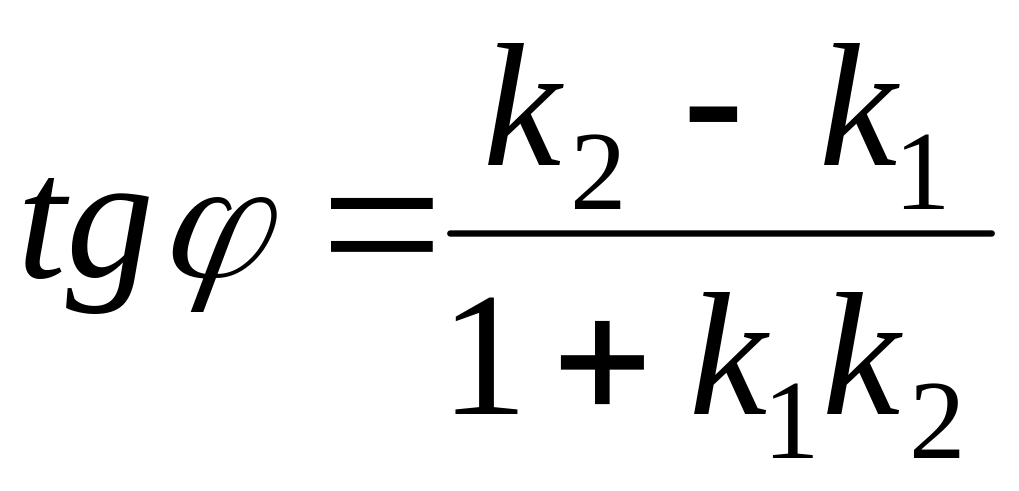.Умовою паралельності двох прямих є , а перпендикулярності – або Нехай задано пряму р-ням і т. . Відстань від точки від прямої дорівнює: ( –напрям нормального вектора): .

Різні способи задання площини в просторі. Нехай задано т. , вектори –біжуча точка. компланарні мішаний добуток або р-ня площини, яка проходить через т. . Загальне р-ня площини– . Р-ня площини, що проходить через три точки:

(1) (3). р-ня площини у відрізках на осях. Р-ня площини, що проходить через дану точку в-ру(напряму): , . Задані дві площини , нормальні в-ри: . Отже, . Умова площин – . Умова || площин – . Відстань від точки від площини (П): знах. за ф-лою 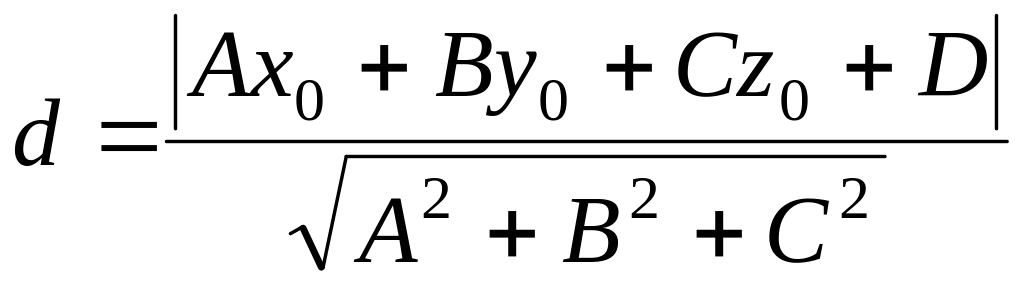. Нехай площина П і пряма задані р-ми: і . кут між нормальним в-ром площини П і напрямним в-ром прямої . Кут між прямою і площиною: . Якщо || П, то , тому , тобто – умова паралельності прямої і площини. Якщо П, || , тому умова перпендикулярності прямої і площини.

2. Лінії другого порядку: еліпс, гіпербола, парабола. Їх основні властивості та зображення.

Алгебраїчне рівняння задає на площині якусь лінію. Наприклад: , Загальне р-ня лінії 2-го порядку:

Еліпс

Еліпсом назив. множина всіх точок площини, сума відстаней від яких до двох фіксованих точок є величина стала. Розгл. на мн. 2 точки, відстань між якими .

, - стала, , -?, - координати точок

– канонічне рівняння еліпса (1)

Властивості

1)Лінія симетрична відносно координатних осей і поч. координат.

2)Всі точки еліпса лежать в прямокутнику:

3) Точки перетину з осями

Ці точки називають вершинами еліпса.

4) В першій чверті з (1): . Це означає, що

у I-й чверті графік спадає.

- параметричне р-ня еліпса.

. .

Гіпербола

Гіперболою називається множина всіх точок площини різниця відстаней від яких до двох фіксованих точок є величина стала

На площині розглядають точки на відстані . , . .

Властивості

1. Лінія симетрична відносно координатних осей і початку координат

2. В смужці –a<x<a точок лінії немає

3. - вісь y не перетинає; y=0 , – вершини гіперболи

4. - 2–і асимптоти гіперболи, . Якщо . –директриси гіперболи. Якщо то - рівностороння гіпербола ( )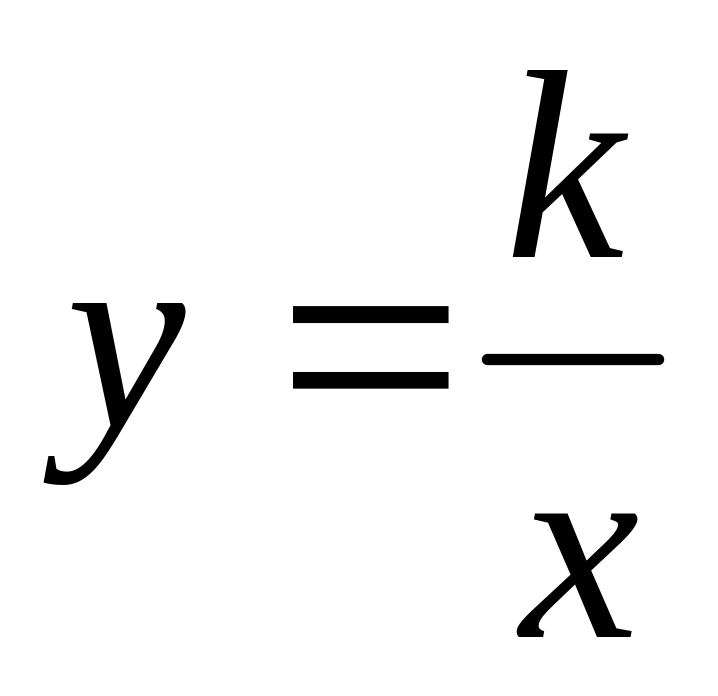

Парабола

Парабола – це множина усіх точок на площині, рівновіддалених від даної точки і прямої.

- директриса.

– канонічне р-ня параболи

Властивості

1. Симетрична відносно Ох.

2. 

3. (0; 0) – єдина точка перетину з осями – вершина параболи, асимптот немає

– ексцентриситет параболи

3. Зведення р-ня кривої другого порядку до канонічного вигляду. Афінна

класифікація кривих 2-го порядку

Спрощення рівнянь центральних ліній ІІ порядку за допомогою інваріантів.

До типу центральних ліній ІІ порядку належать еліпс, гіпербола і пара прямих, що перетинаються. Центр лінії в останньому випадку є точка перетину цих прямих. Коли задана лінія центральна то, щоб звести її р-ня до канонічного вигляду, спочатку, незміюючи напряму осей координат базису, перенесемо його початок в центр лінії. При цьому в р-ні зникають члени першого порядку відносно змінних. Далі повернемо координатний базис так, щоб його осі сумістилися з головними діаметрами, тобто осями симетрії лінії. Після цього перетворення в р-ні зникне член з добутком змінних, тобто р-ня стане канонічним. Але на практиці недоцільно щоразу виконувати всі ці перетворення. Канонічне р-ня лінії можна дістати обчисленням його коефіцієнтів за допомогою інваріантів. Справді, канонічне р-ня центральної лінії ІІ порядку має три члени:

(або два у випадку пари прямих).

Коефіцієнти і при квадратах змінних в р-ні лінії ІІ порядку дорівнюють розв’язкам його характеристичного р-ня , а вільний член за формулою .

Отже розв’язавши характеристичне р-ня і визначивши вільний член , ми відразу можемо написати канонічне р-ня центральної лінії Коли , тобто коли лінія ІІ порядку не вироджена, легко визначити її параметри . Справді, . Отже, форма і розміри лінії відомі. Щоб знайти положення лінії і накреслити її, треба визначити координати центра і скласти р-ня осей симетрії. Для гіперболічного треба ще скласти р-ня її асимптот.

Класифікація лінії ІІ порядку.

Розглянемо рівняння 2-го порядку:

із варіантами: (1)

Повернемо с-му корд. на кут , щоб осі набули головних напрямків

(2)

. У р-ні (1) пропаде . Для (1) і (2) виписуємо матрицю і визначник

,

(3)

I. Розглянемо , ( )

А) лінія невироджена,

) - одного знаку; - протилежного–еліпс ; , - одного знаку – уявний еліпс; - різних знаків – гіпербола

Б) - різних знаків – дві прямі, що перетинаються

- одного знаку – дві уявні прямі, що перетинаються у дійсній площині

ІІ.

С)

дві паралельні прямі; дві прямі, що співпадають; дві уявні паралельні прямі

Д) Перенесемо поч. коорд у вершину параболи