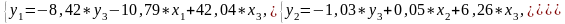Министерство образования и науки РФ

Федеральное агентство по образованию

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Новосибирский государственный технический университет»

Кафедра теории рынка

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №1

«Системы эконометрических уравнений. Основы теории идентификации»

По учебной дисциплине «Эконометрика»

Вариант №2

Выполнили: Аларушкина А., Ларина А., ФБЭ-94

Проверил: Тимофеев В. С.

Новосибирск

2012

Цель: Ознакомиться с основными положениями, понятиями и методами анализа систем одновременных уравнений.

Ситуация 4(2010): «Робинзон на рыбалке». Понимая, что одними утками сыт не будешь, Робинзон раз в неделю ходит на рыбалку. По опыту бывалого моряка он знает, что на его снасти можно поймать кальмаров, сардин или хищных рыб ваху. За долгие годы рыбалки Робинзон заметил, что величина улова каждого вида животных сильно зависит от таких климатических условий как сила ветра (x₁, в футах в секунду), температура воздуха (x₂, в градусах Цельсия) и температуры воды (x₃, в градусах Цельсия). Умудренный эконометрическим опытом, Робинзон считает, что процесс рыбалки может быть описан следующей системой эконометрических уравнений:

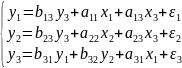
Где y₁ – вес добытых кальмаров; y₂ – вес добытых сардин; y₃ – вес добытых рыб ваху.

y1	y2	y3	x1	x2	x3
44,21	22,20	97,43	1,70	26,00	19,50
49,27	20,06	92,67	0,16	21,80	17,90
48,02	18,66	88,49	0,63	28,00	17,60
…	…	…	…	…	…
44,71	22,58	75,03	5,30	23,80	16,00
47,80	22,60	92,30	1,92	27,70	18,80
44,54	27,50	87,83	6,27	20,30	19,00

Для удобства мы переходим от самих переменных к их отклонениям от средних. Далее под переменной «х» будем подразумевать (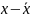 ), а под «у» - (y ).

y1	y2	y3	x1	x2	x3
-1,499	-0,899	12,110	-1,602	-3,415	1,936
3,561	-3,033	7,350	-3,142	-7,615	0,336
2,307	-4,437	3,164	-2,676	-1,415	0,036
…	…	…	…	…	…
-1,001	-0,520	-10,291	1,998	-5,615	-1,564
2,088	-0,493	6,981	-1,382	-1,715	1,236
-1,168	4,404	2,510	2,971	-9,115	1,436

1. Проверить на идентифицируемость каждое уравнение системы.

В данной системе 3 эндогенных и 3 экзогенных переменных. Будем предполагать, что все экзогенные переменные линейно независимы. Проверим второе необходимое условие идентифицируемости для каждого из уравнений:

Проверим уравнение

Н=2 – число эндогенных переменных в уравнении, D=1 – число экзогенных переменных, отсутствующих в данном уравнении, но присутствующих в системе. Так как D+1=1+1=2=H, то уравнение является точно идентифицируемым.

Проверим уравнение

Н=2 – число эндогенных переменных в уравнении, D=1 – число экзогенных переменных, отсутствующих в данном уравнении, но присутствующих в системе. Так как D+1=1+1=2=H, то уравнение является точно идентифицируемым.

Проверим уравнение

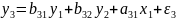
Н=3 – число эндогенных переменных в уравнении, D=2 – число экзогенных переменных, отсутствующих в данном уравнении, но присутствующих в системе. Так как D+1=2+1=3=H, то уравнение является точно идентифицируемым.

Достаточное условие: уравнение идентифицируемо, если по отсутствующим в нем переменным (эндо - и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, ранг которой не меньше, чем число эндогенных переменных в системе минус 1 и определитель которой не равен нулю:

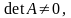
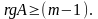
П роверим выполнимость достаточного условия:

Первое уравнение системы: А =

rg (A) = 2, rg (A) = (3-1) достаточное условие выполнено, следовательно, первое уравнение идентифицируемо.

Второе уравнение системы: А =

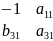
₀ rg (A) = 2, rg (A) = (3-1) достаточное условие выполнено, следовательно, второе уравнение идентифицируемо

Т ретье уравнение системы: А =

rg (A) = 2, rg (A) = (3-1) достаточное условие выполнено, следовательно, третье уравнение идентифицируемо

2. Проверить на идентифицируемость систему в целом.

Так как все уравнения системы точно идентифицируемы, то вся система точно идентифицируема.

3. Преобразовать структурную модель в приведенную.

Структурная модель:

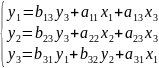
Приведенная форма модели, соответствующая выше упомянутой системе:

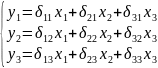, где

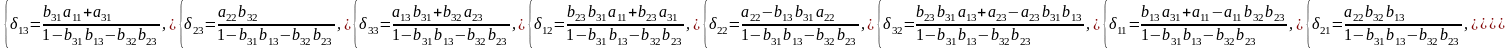
4. Оценить неизвестные параметры системы уравнений с помощью косвенного метода наименьших квадратов.

Наше уравнение в приведенной форме выглядит так:

y ₁= ₁₁x₁+ ₂₁x₂+ ₃₁x₃+ ₁

y₂= ₁₂x₁+ ₂₂x₂+ ₃₂x₃+ ₂

y₃= ₁₃x₁+ ₂₃x₂+ ₃₃x₃+ ₃

О ценим параметры каждого уравнения системы обычным МНК:

= …

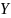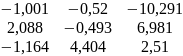
– вектор оценок неизвестных параметров.

Для всех уравнений:

X = …

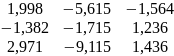
Получаем:

σ11	-0,8421		σ12	1,221095		σ13	-1,18119
σ21	-0,10337		σ22	0,042766		σ23	0,012275
σ31	0,118099		σ32	1,117486		σ33	4,978758

Перевели коэффициенты приведенной формы в параметры структурной модели.

Получили следующие структурные оценки:

a11 -10,7891 a13 42,04484 a22 0,055455 a23 6,264428 a31 -5,01698 b13 -8,42113 b23 -1,03378 b31 1,652225 b32 4,280709

	-0,84	1,22	-1,18
Δ =	-0,1	0,04	0,01
	0,12	1,12	4,98

По приведенной форме получим:

Тогда, используя структурную форму, имеем: